Konikler, düzgün dairesel bir koninin, 3 boyutlu düzlemde, herhangi bir düzlem ile kesişmesi sonucunda ortaya çıkan eğrilerdir.
Bu durumu canlandırmak adına, içi boş bir koniyi boyaya batırılmış bir bıçak yardımıyla kestiğimizi, ardından da boya kurumadan düz bir sayfaya bastırdığımızı düşünelim. Sayfanın üzerinde aldığımız kesitlerin yerleri dolayısıyla rastgele bir biçimde bir çember, elips, parabol veya hiperbol elde edebiliriz.
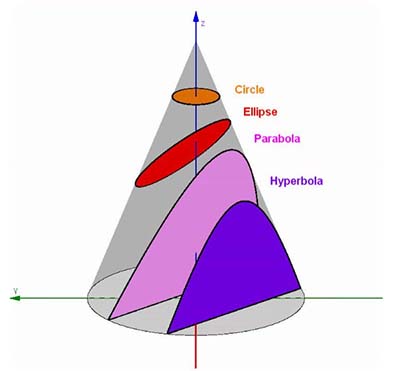

Bir başka deyişle bunları konikler olarak adlandırmamızın temel nedeni, bir koni ile elde edilebilmeleridir.
Konik Nedir?
Koniğin geometrik tanımı; koniğin odak noktasına, doğrultman doğrusuna (directrix) ve koniğin eksantrikliğine (dış merkezliliğine) bağlıdır. Eksantrikliği e, odak noktasını F, doğrultman doğrusunu da d ile gösterirsek; konik üzerinde seçtiğimiz her P noktasının oluşturduğu kümenin gösterimi aşağıdaki gibi olur.
Noktalar = { P : |PF|/|Pd|= e }
Buna ek olarak genel konik denklemini; koniği oluşturan tüm noktaların koniğin doğrultman doğrusuna olan uzaklıklarının, koniğin eksantrikliğiyle çarpılması ve bu değerlerin aynı noktalar için odağa olan uzaklığa eşit olması olarak açıklayabiliriz.
Eksantriklik (Dış Merkezlilik ya da Basıklık)
Türkçeye dış merkezlilik veya eksantriklik olarak kazandırılmış olan bu terim maalesef bize zorunlu eğitim olan ilkokul, ortaokul ve lise dönemlerimizde gösterilmemesiyle beraber aslında bize direkt olarak koniğin çeşidini vermektedir.
Astronomide, özellikle yörünge mekaniğinde eksantriklik yerine basıklık terimi kullanılmaktadır.
Doğrultman doğrumuzu y ekseni ve koniğin odağının bulunduğu, koniğin ekseni olarak tanımladığımız ekseni x-ekseni olarak alalım. Ardından kesişimleri olan O(0,0) noktasına G ve x-ekseninde bulunan koniğin noktasına da P(a,0), odak ve G noktası arasındaki uzaklığa da k diyelim ve kümeyi oluşturduğunu bildiğimiz formülü uygulayalım.
|PF|=|k-a|=|Pd|e = ae
Buradan a=k/(1+e) ve a=k/(1-e) denklemlerini elde etsek de eksantrikliğin bir değerine eşit olduğu durumda ikinci olanak sonuç vermeyeceği için koniğin kendi ekseninde sadece bir tane noktasının olduğunu görebiliriz. Ayrıca, koniğin kendi ekseninde bulunan noktalarına koniğin tepe noktaları ya da tepe noktası deriz.
Yine yörünge mekaniğinde, a değeri yarı büyük eksen uzunluğu olarak tanımlanır.
Görüldüğü üzere, eksantrikliğin bir değerine sahip olduğu konikte sadece bir tepe noktası diğer durumlarda ise iki tane tepe noktası bulunmaktadır. Bu fark üzerinden, tepe noktaları iki tane olan konikler için tepe noktalarının tam olarak ortasındaki noktayı merkez noktası olarak, bu tür konikleri de merkezi konikler olarak adlandırırız.
Parabol
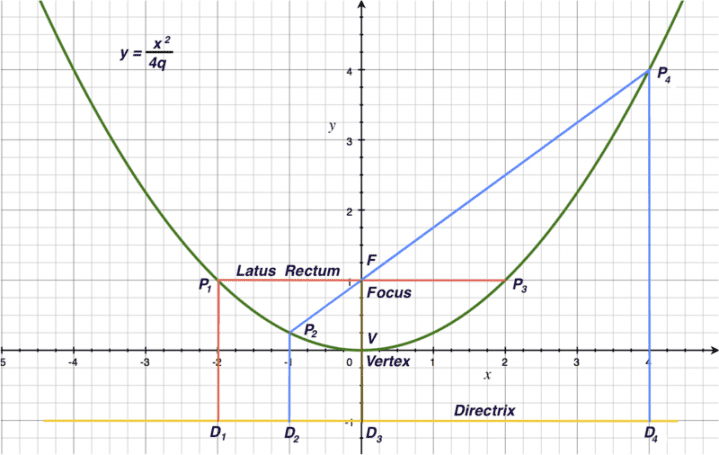
Parabol durumu eksantrikliğin bire eşit olduğu durumdur (e=1). Burada tepe noktası, koniğin ekseniyle doğrultman doğrusunun kesişim noktası ile odak noktasına eşit uzaklıktadır (yani tam olarak ortada). Ayrıca koniğin her noktası doğrultuman doğrusuna ve odak noktasına eşit uzaklıkta olmalı.

Elips
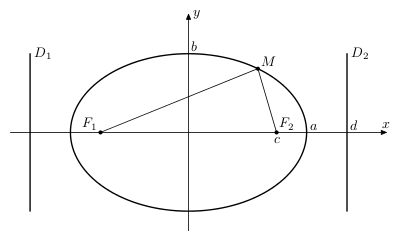
Elips durumu eksantrikliğin sıfır ile bir arasında olduğu durumdur (0<e<1). Stabil bir şekilde yörüngede dolaşan gök cisimlerinin hepsi eliptik yörüngelere sahiptirler ve basıklık (eksantriklik) değerleri genellikle sıfır değerine oldukça yakındır (bkz. Yörünge nedir).
Elips için bir değil, iki tepe noktası bulunur. Bu noktalardan birisi koniğin ekseniyle doğrultman doğrusunun kesişim noktası ve odak noktasının arasındadır. Fakat eksantriklik (e) değeri birden küçük olduğu için odak noktasına daha yakındır.
Örneklendirmek adına, kağıdın sol tarafında doğrultman doğrumuz tam orta kısmında ise odak noktamız olsun ve kağıdı tam ortadan ikiye bölelim. Kağıdın sağ yüzünde bir tepe noktası, sol yüzünde bir diğer tepe noktası olacaktır.

Hiperbol
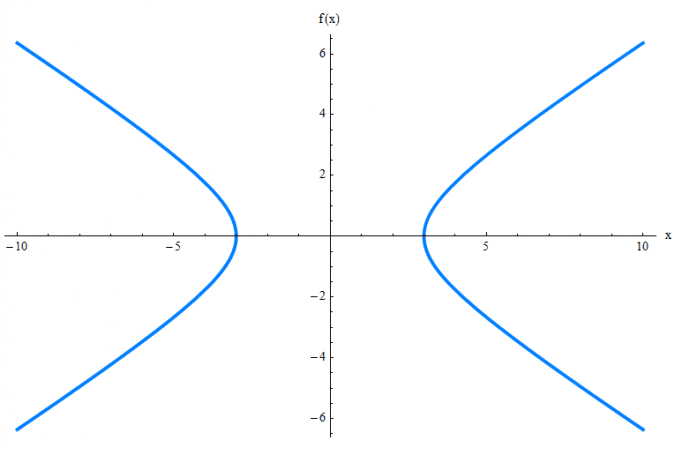
Hiperbol durumu eksantrikliğin bir değerinden büyük olduğu durumdur (e>1). Daha önceki a=k/(1-e) denkleminden de görüleceği üzere, tepe noktasını veren değerlerden birisi negatif bir değer almalı. Bu durumda tepe noktaları, koniğin ekseniyle doğrultman doğrusunun kesişimi olan noktaya göre farklı taraflarda olmalıdır.
Örneklendirmek adına bu sefer doğrultman doğrusunu kağıdın tam orası olarak alıp, kağıdı ikiye böldüğümüzü düşünelim. Kağıdın sağ yüzünde bir tepe noktası, sol yüzünde bir diğer tepe noktası olacaktır.

Merkezi Konikler
Elips ve hiperbol iki tepe noktasına sahip olduğu için merkezi konikler olarak adlandırılır. Her konik kendi eksenine göre simetrik iken, merkezi konikler ayrıca kendi merkez noktalarına göre de simetriktirler. Bu simetriden doğan ve koniğin noktalarının bulunduğu küme tanımına göre merkezi konikler, bir diğer doğrultman doğrusu ve odak noktasına da sahiptir. Buna ek olarak, elipsin iki tepe noktasındaki uzaklığıyla elipsin üzerinde seçeceğiniz herhangi bir noktanın elipsin sahip olduğu iki odak noktasına olan uzaklıklarının toplamı birbirine eşittir.
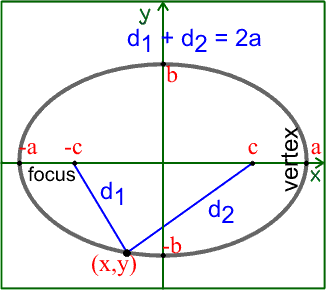

Koniklerin Kanonik Denklemleri
Koniklerin denklem gösterimlerini kanonik denklemlerle yapabiliriz. Öncelikle parabol için düzlemin merkez noktası O(0,0)’ı parabolün tepe noktası olarak alalım. Odak noktasının x-ekseninde veya y-ekseninde olmasına bağlı olarak denklem değişecektir. Odak noktası F(c,0) yani x-ekseninde iken x=y2/(4c); odak noktası F(0,c) yani y-ekseni üzerindeyken ise x2=y(4c)’dir. Tabii ki iki gösterimde de orijin noktası parabolün tepe noktası olmalıdır.
Merkezi konikler için ise düzlemin başlangıç noktası olan orijini koniklerin merkez noktası, yani iki tepe noktasının ortasını, seçersek tepe noktaları x-eksenindeyse biri V(a,0) diğeri ise merkez noktasına göre simetriklikten kaynaklı V'(-a,0) olur. Durum y-ekseninde sırasıyla V(0,a) V'(0,-a) olacaktır. Biz bu a değerini odak noktasının orijine olan uzaklığının koniğimizin eksantriklik değerine bölümü olarak seçersek koniğin sahip olduğu noktalar kümesi tanımından elips için;
Tepe noktaları x-ekseni üzerindeyken
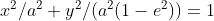
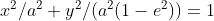
ve tepe noktaları y-ekseni üzerindeyken
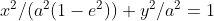
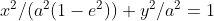
kanonik denklemlerini elde etmiş oluruz. Aynı durumu hiperbol için sağlarsak:
Tepe noktaları x-ekseni üzerindeyken
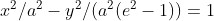
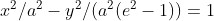
ve tepe noktaları y-ekseni üzerindeyken
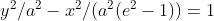
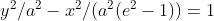
kanonik denklemlerini elde ederiz.
Hazırlayan: Barış Şahin
Editör: Ögetay Kayalı
Referanslar
- Ali Doğanaksoy, Ortadoğu Teknik Üniversitesi Matematik Bölümü, Analitik Geometri ders notları
- Halil İbrahim Karakaş, Analytic Geometry
Kapak Görseli: https://brilliant.org/wiki/conic-sections/
