Işığın doğasını ve çevresiyle olan etkileşimini anlamaya çalışacağımız bu yazı dizimize, milattan önce 2.yüzyılda yaşamış olan İskenderiye’li Heron’un görüşleri ile başlayacağız ve ardından, 17. yüzyıla atlayıp Fermat prensibini konuşacağız. Son olarak da Fermat prensibini kullanarak Snell yasasını türetmeye çalışacağız.
Heron’a göre, ışık iki nokta arasında ilerlerken en kısa yoldan ilerler. Eğer ortamlar aynıysa, ışığın takip edeceği yol bu iki noktayı birleştiren doğru parçasıdır.
Benzeri bir yorumu yansıma için yaparsak, aşağıdaki figürde A noktasından çıkan ışığın hangi yolu takip ederek B‘ye ulaşacağını bulabiliriz.
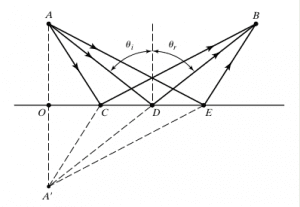
A‘dan çıkıp yansıyan ışığın B‘ye nasıl ulaşacağını bulmak için, A noktasının yansımasını alabiliriz. Bu noktaya A’ diyelim. A’den B‘ye giden en kısa yol, bize yansıyan ışığın izleyeceği yolu verecektir. Öyleyse ışık, ADB yolunu izleyerek yansımayı gerçekleştirir.
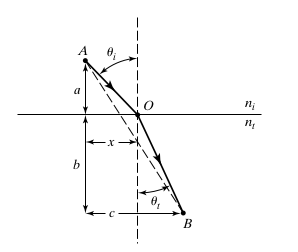
Peki ya, ışık yansıma değil de kırılma yaparsa? O zaman da en kısa yolu mu takip eder?
Görünen o ki durum pek de öyle değil. Çünkü yukarıdaki görselde en kısa mesafe kesik çizgilerle gösterilmişken; gözlemlerimiz bize ışığın AOB‘yi takip ettiğini söyler.
Şimdi, bu probleme cevap bulmak için zamanda biraz daha ileriye, 17. yüzyıla gidelim. Pierre de Fermat isimli Fransız matematikçi, Heron’un bu fikrini genelleştirir ve kırılma olayını da açıklayabilir hale getirir.
Ancak, ne yazık ki tıpki Heron prensibinde olduğu gibi, Fermat prensibinin de doğru sonucu vermediği örnekler vardır. Fermat prensibinin daha geniş bir uygulama alanına sahip olması için, tanımda (başka bir yazıda konuşacağımız) ufak değişiklikler yapılması gerekir.
Fermat’ın ortaya attığı prensibe geri dönecek olursak; Fermat, Heron’un prensibini daha özel bir hale getirerek, “ışık, iki nokta arasındaki en kısa yolu takip etmez. Işık, iki nokta arasını en kısa sürede alacağı yolu takip eder” der.
Yani, eğer ki ışık ikinci bölgede daha yaval hareket etmekteyse; ışık, en kısa sürede diğer noktaya ulaşacağı şekilde bükülür. Bu sayede A ve B noktası arasındaki toplam süre minimuma indirgenmiş olur.
Snell Yasasının Türetilmesi
Yazımızın bu kısmında ise, bu prensibi kullanarak Snell yasasını türetmeye çalışacağız.
Eğer temel fizik bilgilerimizi aklınıza getirirseniz, iki nokta arasında hareket eden cismin yolculuk süresini, yol/hız ile bulabileceğimizi hatırlarsınız. Öyleyse, ışığın izlediği yol için geçen toplam süreyi yazacak olursak;
Burada vi gelen ışığın hızını, vt ise kırılan (geçen) ışığın hızını ifade etmektedir. AO ve OB için pisagor bağıntısını yazar ve yerine koyarsak, denklem aşağıdaki hali alır:
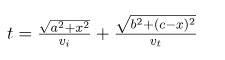
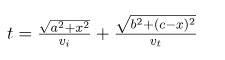
“Işığın minimum sürede diğer noktaya ulaşması” fikrini matematiğe uyarlamak istersek, her iki bölgede de bunu mümkün kılmak için ayrı ayrı alınan yolu minimum hale getirmemiz gerektiğini söyleyebiliriz.
Bu da, aslında yola (x’e) göre türev alıp bunu sıfıra eşitlemekten başka bir şey değildir (ayrıntılarını türev ve integral hakkında yazacağımız yazılarda konuşacağız).
Öyleyse, yukarıdaki ifadenin yola göre türevini almamız ve sıfıra eşitlememiz, bizlere minimum süreyi verecektir. Biraz kalkülüs kullanarak, yukarıdaki denklemden aşağıdaki denklemi elde edebiliriz.
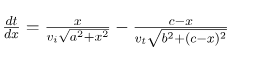
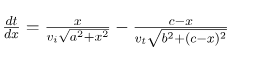
Şimdi, yukarıdaki figürde verilen Θ açıları için sinüs ifadelerini yazalım.
Görebileceğimiz gibi, bu sinüs ifadeleri, eşitliğimizin sağ kısmıyla birebir aynıdır. Öyleyse, yukarıdaki denklemimize ufak bir düzenleme yapabiliriz.
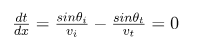
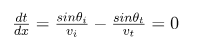
Bu eşitliği basitleştirirsek, 
Biliyoruz ki, v dediğimiz şey; ışık hızının, ortamın kırıcılık indisine bölümü. Yani v=c/n. Bunu da yerine yazarsak, Snell yasasını elde etmiş oluruz.
Bu sayede, ışığın geliş açısı ve çıkış açısı arasındaki ilişkiyi veren Snell yasasını türetmiş olduk.
Ege Can KARANFİL
Referanslar
1.Frank L Pedrotti, Leno M Pedrotti, Leno S Pedrotti, “Introduction to Optics”, 3rd Edition, Chapter 2.2
2.HyperPhysics,”Fermat’s Principle:Reflection” <http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/Fermat.html>
Kapak Görseli: 1.au, “Power of Optics” <https://www.youtube.com/watch?v=4nCIzPuLYJA>
