Özel Görelilik: Uzunluk Büzülmesi ve Müonlar

- Özgün
Kararsız bir yapıya ve yalnızca 2.2 µs (mikrosaniyelik) yaşam ömrüne sahip olan müonların oluşum hikayesi ise şöyledir: Dünya'ya gelen kozmik ışınların (genellikle yüksek enerjili protonların), Dünya'nın atmosferinin üst katmanlarında atom çekirdeğiyle etkileşime girmesiyle, pionlar oluşmakta; saçılan pionlar da bu yazımıza konu olan müonlara bozunmaktadır.
Yalnızca 2.2 µs'lik ömre sahip olan müonların hızları, ışık hızının neredeyse %99.8'ine eşittir. Müonlar bu kısacık ömürlerinde, böylesine yüksek hızlarıyla ancak 10 kilometrelik bir yolculuk yapabilirler. Bunu bilmemizi sağlayan şey, müon dedektörlerinin her bir dakikada bir santimetrekareden bir tane müon geçtiğini ölçmeleridir.
Ancak, ufak bir hesap yaparsanız göreceksiniz ki bu kısacık ömründe, böylesine yüksek bir hıza sahip olmalarına rağmen, sadece (2.994x108)(2.2x10-6) = 0.66 km yol alabilmeleri gerekmektedir. Peki, nasıl oluyor da biz müonları yaklaşık 10 kilometrelik yolculukları sonrasında, deniz seviyesinde gözlemleyebiliyoruz? Bir yerlerde hata mı yapıyoruz?
Zaman Genişlemesini Kullanarak Açıklamak
Evet hata yapıyoruz çünkü, özel göreliliğin bizlere söylediği gibi ışık hızına yaklaştıkça zaman bizim için ilk referans aldığımız yere göre yavaş akmaktadır. Müonun sahip olduğu böylesine yüksek hızlarda, bu etkiyi oldukça rahat görebiliriz.Biz biliyoruz ki müonun yaşam ömrü olan 2.2 µs, müon'un 2.994x108 m/s hıza sahip olan referans sisteminde ölçülmektedir. Şimdi, özel göreliliğin bizlere söylediği zaman genişlemesini hesaba katalım ve bakalım, hesaplarımız bu sefer bizi haklı çıkartacak mı?
Dünya'dan, müonun hareketini gözlemleyen bizim için geçen zaman t olsun. Müon için gecen zaman da t0olsun. Zaman genişlemesi denklemini ifade edecek olursak;
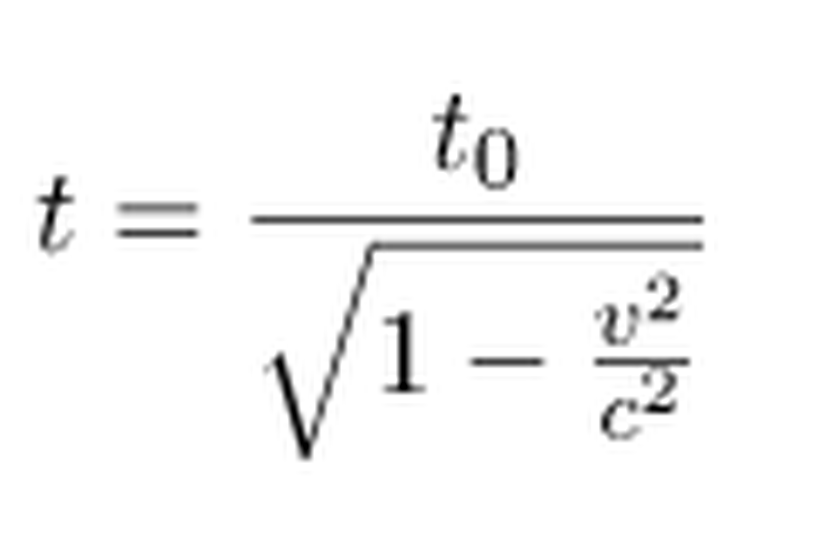
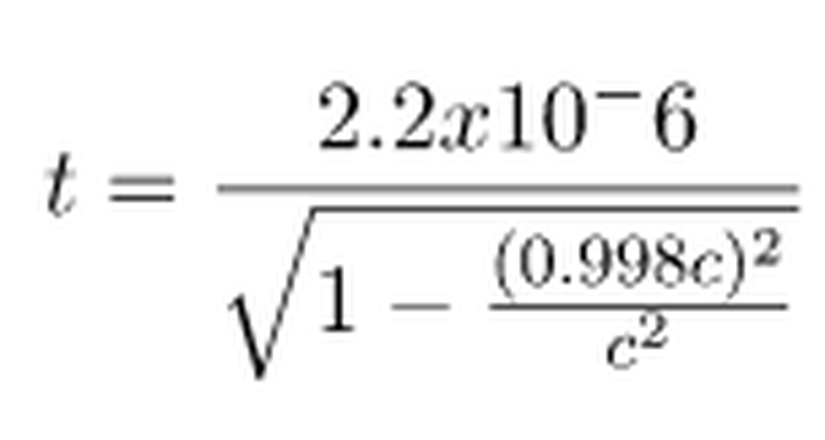
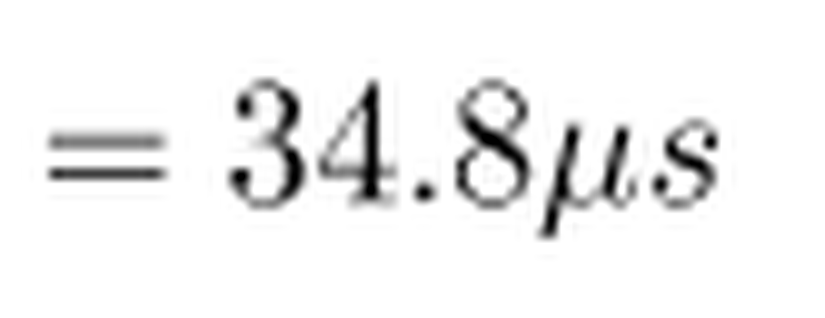
Özetle bütün mesele, özel göreliliği hesaba katmadan hesap yapıyor oluşumuzdaymış! Yani müonların gözlenmesi, aslında özel göreliliğin naçizane bir ispatıdır.
Uzunluk Büzülmesini Kullanarak Açıklamak
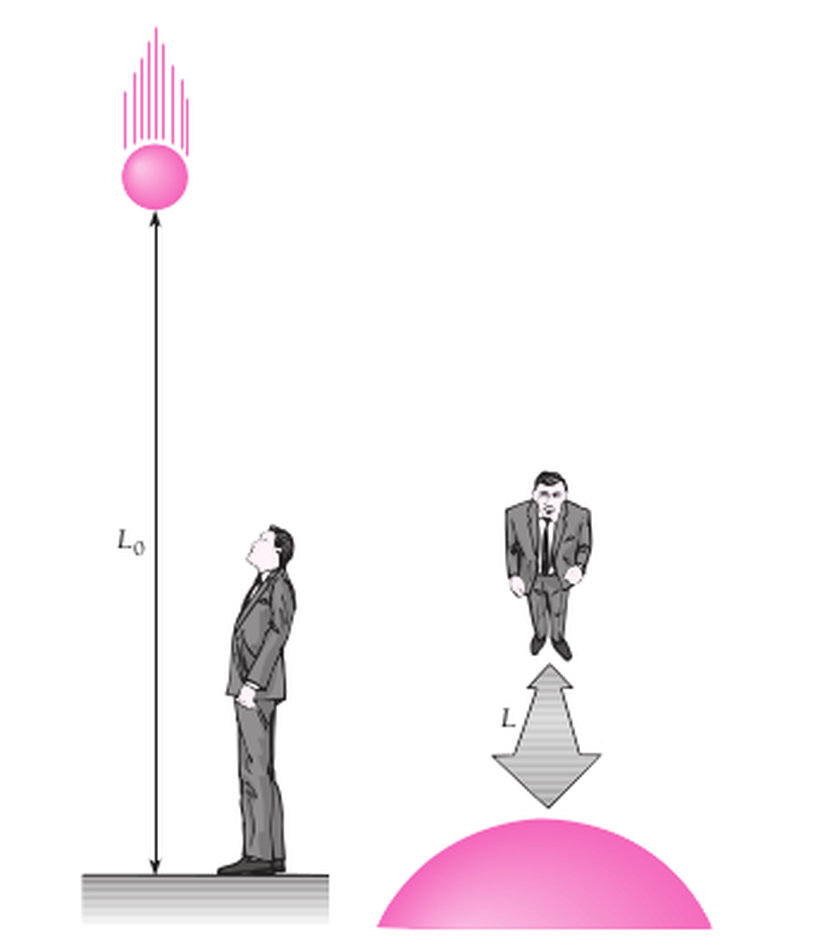
Şimdi biliyoruz ki, yaşam ömrü 2.2 µs olan müonumuz, yalnızca 0.66 km yol alabilir. Peki, şimdi bunu nasıl açıklayacağız? Diğer çerçeveden baktığımızda zaman genişlemesiyle olayı çözebiliyorduk, fakat müonun çerçevesinden baktığımızda ne olacak? Uzunluk büzülmesi... Bu sefer müonun önündeki yol büzülecek.
İkimiz de aynı hızda hareket ettiğimiz için, zaman ikimizde de aynı akmaktadır. O zaman... Müonun referans sistemindeki 0.66 km, Dünya'daki bir gözlemci için 10.4 kilometreye mi denk gelmektedir? Cevap koca bir evettir!
Diyelim ki Dünya'daki bir gözlemci için, müonun aldığı yol L0 olsun. Müonun sırtında yolculuk yapan diğer gözlemci için de L olsun. Öyleyse (zaman genişlemesinin tam tersinin olmasını beklediğimiz için), yukarıdaki ilişkiyi matematiksel olarak aşağıdaki gibi ifade edebiliriz:
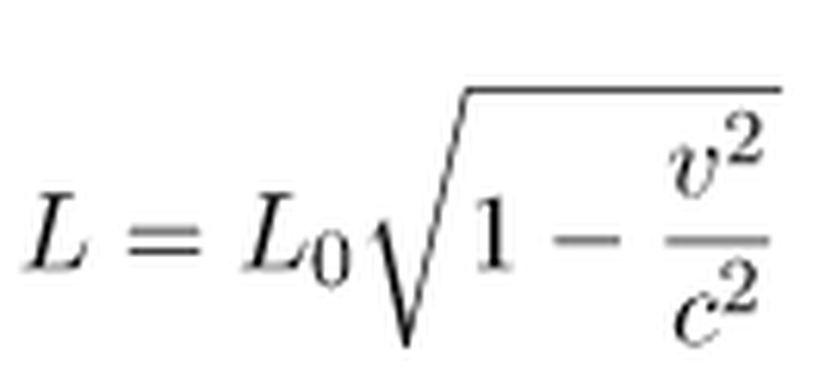
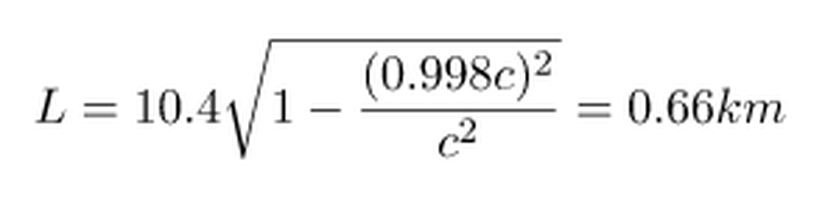
Sonuç
Bizler eğer ışık hızına yakın hızda hareket eden bir cismi gözlemlersek, gözlemlediğimiz cismin referans sisteminde geçen zaman bizde geçen zamandan daha kısa olur. Mesela bizim müon örneğimizde gözlemcide geçen 34.8 µs, hareket eden cisimde geçen 2.2 µs'ye denktir. Keza Dünya'dan bakan bir gözlemcinin gördüğü uzunluk ile müonun gördüğü uzunluk da farklıdır. Müon için uzunluk büzülmesi gerçekleşmiş ve 10 km'lik yol 0.66 km olmuştur.Hareket eden cisim bu zaman farkından dolayı, bizim referans sistemimizde t kadar sürede x kadar yol katettiğinde, kendi referans sisteminde x'ten daha az bir mesafe katetmiş olur. Lakin ikisinde de ulaştığı nokta aynıdır. Yani gözlemcilerin sonuçları birbiri ile çelişmez.
Özel Görelilik Hakkındaki Diğer Yazılar
Özel Görelilik: Göreliliğin YorumlanmasıÖzel Görelilik: Göreli Olma Durumu
Özel Görelilik: İkizler Paradoksu ve Eşzamanlılığın Göreliliği
Özel Görelilik: Mıknatıs İlişkisi
Hazırlayan:Ege Can Karanfil
Düzenleyen ve Geliştiren: Ögetay Kayalı
Referanslar
1. Arthur Beiser, "Concepts of Modern Physics" , 6th Edition
2. M. Bilge Demirköz, Modern Fizik ders notları
3.https://nmi3.eu/muon-research/characteristics-of-muons.html
4.https://www.isis.stfc.ac.uk/Pages/What-is-a-muon.aspx
Görsel Kaynakları
1.Arthur Beiser, "Concepts of Modern Physics" , 6th Edition, Sayfa 16
Kapak Görseli
Phys.org, <https://phys.org/news/2018-05-standard-particle-physicsthe-absolutely-amazing.html>
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 29/04/2024 10:51:06 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12661
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.



