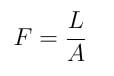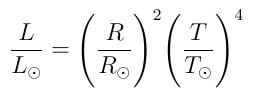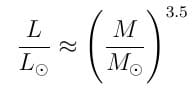Lüminozite (ışıtma) kabaca, gök cisminden birim zamanda saçılan enerjinin bir ölçütüdür. Elbette bir cismin ışıtması, aynı zamanda onun parlaklığı ile de doğrudan ilişkilidir.
Gök cisimleri, gerek termal süreçlerle gerekse termal olmayan süreçlerle bir ışınım üretirler. Şüphesiz ki onları bu sayede görebiliyoruz. Bu sebeple en büyük ölçüm olanağımız onlardan gelen ışığı incelemek olduğu için, gelen ışık üzerinde çeşitli hesaplamalar yapmamız gerekir. Görünür parlaklık, ölçebildiğimiz bir nicelik olduğundan ve uzaklıkla azaldığından dolayı, cismin uzaklığının bilinmesi durumunda salt parlaklığa ulaşabiliriz. Böylelikle cismin lüminozitesi (ışıtması) hakkında da bilgi edinmiş, dolayısıyla ona bu ışıtmayı veren fiziksel arkaplan hakkında da bilgi edinmiş oluruz.
Kara cisim üzerine Stefan-Boltzmann eşitliği uygulanırsa, bir kara cismin yaptığı ışıtma bulunur. Bu cisim kusursuz bir biçimde opak ve hiçbir şeyi yansıtmayan bir cisimdir (bkz. Yıldız Astrofiziği: Kara Cisim Işıması). Böylelikle lüminozite (ışıtma) aşağıdaki şekilde ifade edilir.
Burada σ (sigma) Stefan-Boltzmann sabiti, A alan, T ise Kelvin cinsinden sıcaklıktır. σ’nın değeri ise 5.67×10-8 W.m-2 K-4‘tür.
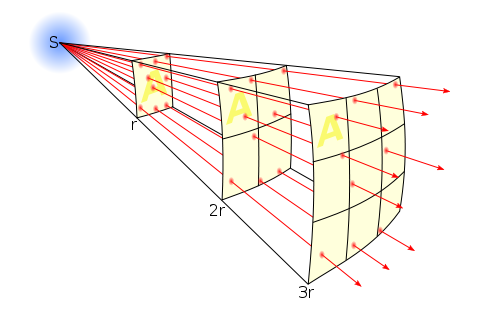

Kaynağın bir an için noktasal bir kaynak olduğunu düşünelim. Her doğrultuda eşit miktarda olmak üzere bir ışıma yapacağından, etrafında aslında ışıktan bir küre oluşturur. Bu kürenin yarıçapı arttıkça, birim alan başına düşen ışık miktarı azalacaktır. Ölçümlerimizde elde ettiğimiz, deneyimlediğimiz durum bu olduğundan, böyle bir tanımlama da yapmamız gerekir. F, akı yoğunluğu olarak adlandırılmak üzere;
olarak ifade edilir. Burada A, aydınlatılan yüzeyin alanıdır. Bir kürenin yüzey alanı A=4πR2 olduğuna göre, yıldızlar için ışıtmayı aşağıdaki şekilde ifade edebiliriz.
Burada R yıldızın yarıçapı, T ise yüzey sıcaklığıdır (bazen etkin sıcaklık olarak da alınır).
Güneş ile diğer cisimler arasında bir ilişki yakalamak için, Güneş cinsinden orantı kurabiliriz. Bu durumda sabitler birbirini yok eder ve ifade aşağıdaki hali alır.
Ayrıca anakol yıldızları için kütle ile ışıtma arasında da aşağıdaki gibi bir bağlantı bulunur.
Burada ⊙ sembolü, Güneş’i ifade etmek için kullanılır. Bu alt indise sahip değerler, Güneş’in ilgili değerleridir.
Güneş’in ışıtması (L⊙) 3.846 x 1026 W’dır. 1 Watt birimin 107 erg s-1 biriminde olduğunu hatırlayın. Yani bir başka deyişle Güneş’in ışıtması 3.846 x 1033 erg s-1‘dir.
Ögetay Kayalı
Referanslar
1. Evren S., Ege Üniversitesi Astronomi ve Uzay Bilimleri, Astronomiye Giriş
2. De Boer, K. ., & Seggewiss, W. (2008). Stars and Stellar Evolution.