Kara Cisim Işıması Nedir?

- Özgün
- Fizik
Termodinamik dengede bulunan bir kara cismin, yalnızca sıcaklığından ötürü yaptığı ışımaya kara cisim ışıması (ya da siyah cisim ışıması) denir. Kara cisim ise; üzerine düşen tüm ışınımı soğuran ve hiçbirini yansıtmayan, bu sebeple de kara olması gerektiğini ön gördüğümüz, tamamen varsayımsal bir cisimdir. Yapılan bu ışımayı inceleyip matematiksel olarak ifade ettiğimiz fonksiyon Planck dağılım fonksiyonudur.
"Kara cisim ışıması nedir?" sorusunu cevaplamak ve anlamlandırmak biraz zor olabilir. Lakin bu olay fiziksel birçok olgunun temelinde yatar. Eğer kara cisim ışımasının ne olduğunu tam olarak anlayabilirseniz, fizik alanında ufkunuz genişleyecektir.
Daha basit bir ifadeyle kara cisim ışımasını (ya da siyah cisim radyasyonunu) açıklamaya çalışalım. Burada öncelikli olarak bilinmesi gereken ışıma kelimesinin aslında radyasyon ile aynı olduğudur. Genellikle radyasyon denilince akla sağlığı tehdit eden iyonize edici radyasyon gelir, fakat radyasyon sadece bundan ibaret değildir. Gördüğümüz ışık dahil tüm elektromanyetik spektrum bir radyasyondur. Eğer bu konu kafanızı karıştırıyorsa, elektromanyetik spektrum konusuna göz atmakta fayda var.
Kara Cisim Işımasının Doğası
Kara cisim ışıması, özetle şunu söyler: Her cisim, var olan sıcaklığından ötürü bir ışıma yapar.
Fakat yapılan bu ışıma farklı dalga boylarında, farklı şiddettedir. Nispeten sıcak cisimler daha ziyade moröte (ultraviyole) bölgede ışıma yaparken, nispeten soğuk cisimler ise daha çok kızılöte (infrared) bölgede ışıma yapar. Buna ek olarak cismin sıcaklığı arttıkça her bölgede yaptığı ışıma da artmaktadır. Yani soğuk cisimler, en fazla ışımalarını kızılötede bölgede yapıyor; fakat sıcak cisimler kızılöte bölgede soğuk cisimlerden de daha çok ışıma yapıyor. Ancak sıcak cisimler kendi içlerinde en baskın olarak morötede daha fazla ışıma yapıyor.
Bu sebeple soğuk yıldızlar kırmızı görünürken, sıcaklık arttıkça yıldızların rengi önce sarıya ardından beyaza ardından da maviye doğru gidiyor. Biraz karmaşık görünen ifadeler olduğunun farkındayım. İşe biraz matematiksel açıdan yaklaşırsak yorumlamak çok daha kolay olacaktır.
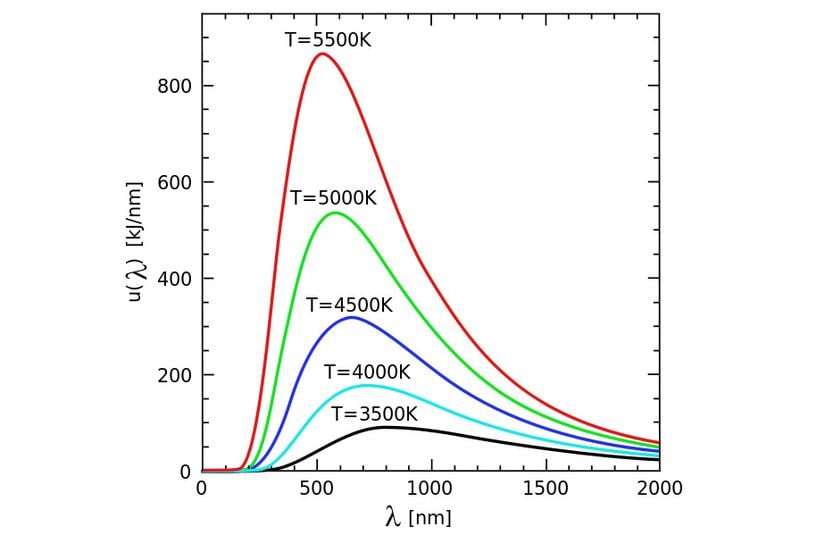
Yukarıdaki grafikte yatay eksen dalga boyunu gösteriyor. Soldan sağa doğru gidildikçe dalga boyunun arttığına yani enerjinin azaldığına dikkat edin. Yatay eksende solda kalan bölüm, yüksek enerjili taraf olduğu için, basitçe moröte taraf olarak adlandıracağım. Aslında orada X ışınları gibi birçok ışıma daha var, fakat görsel bölgede maviden sonra geldikleri için basitçe morötesi demeyi anlatım kolaylığı açısından uygun görüyoruz. Dolayısıyla yatayda sağda kalan bölge de yine radyo dalgaları gibi farklı dalgaları barındırsa da oraya da basitçe "kızılötesi bölge" diyeceğiz. Dikey eksende gördüğümüz değer ise yapılan ışımanın yeğinliğini, yani basitçe miktarını belirtiyor.
Sıcaklık ve Kara Cisim Işıması İlişkisi
Siyah ile gösterilen 3500 K sıcaklığa sahip olan bir cismin, yaptığı ışımanın maksimum dalga boyuna dikkat edin. Bu dalga boyu, 4000 K olan cismin yaptığı ışımanın, maksimum olduğu dalga boyundan daha uzun dalga boyuna denk düşer. Sıcaklık arttıkça tepe noktasının sola kaydığını, yani sıcaklık arttıkça en fazla yapılan ışımanın dalga boyunun kısaldığını görürüz. Bir başka deyişle sıcaklık arttıkça, en fazla yapılan ışımanın enerjisi de artmaktadır. Bir diğer dikkat çekici nokta ise, sıcaklık arttıkça tüm bölgelerde yapılan ışımanın arttığıdır. Bu konuda daha fazla bilgi için Wien Yasası yazımızı okuyabilirsiniz.
Tam olarak bu sebeplerden ötürü, ısıttığınız bir cisim önce kırmızı görünmeye başlar. Çünkü gözümüzün görme aralığına denk düşen en düşük enerjili ışıma kırmızı renge karşılık gelir. Ardından ısıtmaya devam ettikçe cismin yapacağı ışıma kırmızı bölgede artacaktır. Bu daha kızıl olmasına sebep olmalı diye düşünebilirsiniz. Fakat daha yüksek enerjili mavi bölgede yapacağı ışıma, kırmızı bölgede yapacağından çok daha fazla artar. Dolayısıyla hali hazırda kırmızı görünen cisme bir de mavi renk eklenir. Tüm renkleri karıştırırsanız elde edeceğiniz renk beyaz olduğundan, eşitlik durumunda cisim beyaz görünecektir. Eğer biraz daha ısıtır ve mavi bölgede yaptığı ışımayı artırırsanız, beyaza mavi eklendiği için mavi görünmesine sebep olursunuz.

Yukarıdaki fotoğrafta, ısıtılan bir demirde bunun harika bir örneğini görüyoruz. Demirin en çok ısınan bölgesi yüksek sıcaklığı sebebiyle beyaz görünürken, giderek aşağıya doğru daha soğuk olan bölgeleri sarı, ardından da kırmızı olarak görüyoruz. Burada gördüğümüz olay, doğrudan kara cisim ışımasına bir örnektir. Fakat buradaki cismin bizim varsaydığımız gibi bir cisim olmadığını da unutmayın.
Kısaca Kara Cisim Işıması
Özetle, kara cisim ışımasıyla ilgili şu noktaları vurgulayabiliriz:
- Her cisim sıcaklığından ötürü bir ışıma yapar.
- Bu ışımanın bir maksimum noktası bulunur.
- Cismin sıcaklığı arttıkça maksimum noktası, yüksek enerjili tarafa doğru kayar (Wien kayma yasası).
- Cismin sıcaklığı arttıkça her bölgede yaptığı ışıma artar.
- Bu nedenle ısınan cisim önce kırmızı, ardından sarı, ardından beyaz, ardından da mavimsi tonlarda görünür.
Isınan bir demir bu nedenle kızarır, ardından sararır. Aynı sebepten ötürü hiç yeşil yıldız yoktur.
Teori vs. Pratik
Her madde doğası gereği, yukarıda paylaştığımız gibi pürüzsüz bir eğri vermek yerine, bu eğrinin üzerinde girintiler çıkıntılar olan bir eğri verir. Hiçbir cisim asla böyle pürüzsüz bir eğri vermez. Örneğin aşağıdaki görsel, Güneş'in spektrumuna aittir. Buradaki girintiler, Güneş'ten yayılan fakat oradaki gazlarla etkileşime girdiği için bir takım soğurulmaya (absorption) maruz kalan dalga boylarını işaret eder.
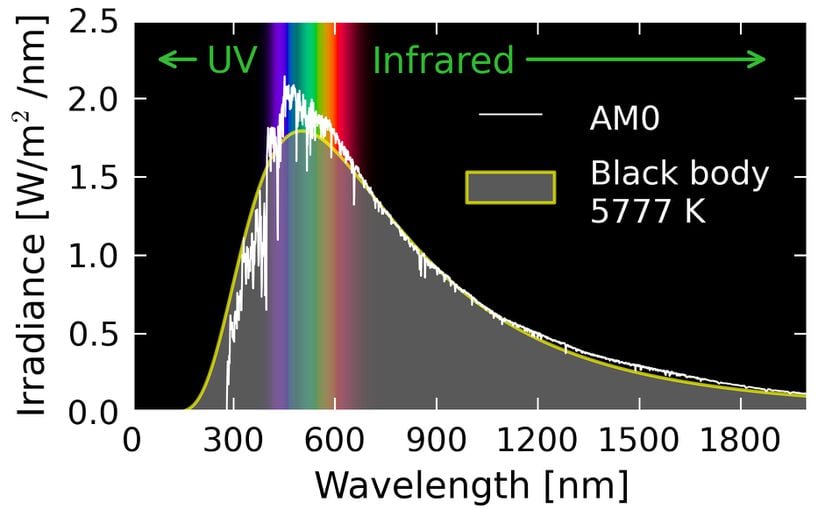
İleri Okuma: Kara Cisim Işıması Formülleri
Planck Fonksiyonu
hh Planck sabiti, cc ışık hızı ν\nu frekans, TT sıcaklık, kBk_B boltzmann sabiti olmak üzere Planck fonksiyonu aşağıdaki gibi verilir.
Bν(T)=2hν3c21ehνkBT−1\Large B_{\nu}(T) =\frac{2h\nu^3}{c^2}\frac{1}{e^{\frac{h\nu}{k_B T}}-1}
Birimi W⋅sr−1⋅m−2⋅Hz−1\text{W}\cdot \text{sr}^{-1} \cdot \text{m}^{-2} \cdot \text{Hz}^{-1}'dir.
Wien Yaklaşımı
Şu eşitsizlikten yola çıkarsak:
hνkT≫1\Large \frac{h\nu}{kT}\gg 1
Şunu yazabiliriz:
ehνkT−1≈ehνkT\Large e^{\frac{h\nu}{kT}}-1\approx e^{\frac{h\nu}{kT}}
Bu durumda Planck fonksiyonu aşağıdaki gibi yazılabilir.
Bν≈2hν3c2e−hν/kT\Large B_{\nu} \approx \frac{2h\nu^3}{c^2}e^{-h\nu/kT}
Rayleigh Yaklaşımı
Tam tersine bakalım:
hνkT≪1\Large \frac{h\nu}{kT}\ll 1
Bu eşitsizlik için Taylor serisini açtığımızda:
Bν≈2ν2kTc2\Large B_{\nu} \approx \frac{2\nu^2 kT}{c^2}
elde edilir.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
İçerikle İlgili Sorular
Soru & Cevap Platformuna Git- 12
- 8
- 5
- 4
- 3
- 3
- 3
- 0
- 0
- 0
- 0
- 0
- K. D. Boer. (2012). Stars & Stellar Evolution. ISBN: 9782759803286. Yayınevi: EDP Sciences.
- UCSD. Black Body Radiation. Alındığı Tarih: 1 Aralık 2022. Alındığı Yer: UCSD | Arşiv Bağlantısı
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 16/04/2024 08:16:15 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12866
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.





