Kuantum mekaniğinin temellerini anlamak için anlaşılması gereken en önemli noktalardan birisi, zamandan bağımsız Schrödinger denklemidir. Bu yazımızda da, zamandan bağımsız Schrödinger denkleminin nasıl türetildiğini inceleyeceğiz.
Karşımıza çıkan denklemin çözümü de parçacığın durumuna dair pek çok bilgiyi içinde barındıran dalga fonksiyonunun (ψ) çözümü olmuş olacak. Öncelikle herhangi bir V(x,t) potansiyeli için yazılmış olan zamana bağlı dalga denklemini hatırlayalım.
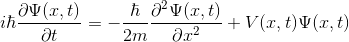
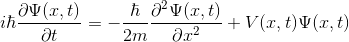
Zamandan Bağımsız Schrödinger Denkleminin Türetilişi
Eğer ki potansiyelin zamandan bağımsız olduğunu kabul edersek, yani V(x) olarak ifade edersek, değişkenlere ayırma yöntemini kullanarak bu kısmi diferansiyel denklemi rahatlıkla çözebiliriz. Değişkenlere ayırma yöntemine göre, diyebilliriz ki:
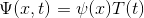
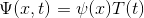
Öyleyse,
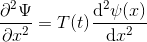
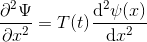
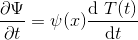
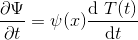
Olarak yazabiliriz. Şimdi bu iki denklemi, zamana bağlı Schrödinger denkleminin içine yazalım.
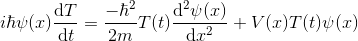
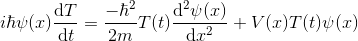
Şimdi eşitliğin iki tarafını ψT’ye bölelim.
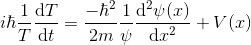
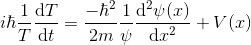
Karşımıza çıkan bu denklem, bizi ona baktıkça bizi mutlu eden türden bir denklemdir. Sebebi ise oldukça basit. Eşitliğin sol tarafı t’ye, sağ tarafı ise x’e bağlı bir fonksiyon halindedir. Bu da demek oluyor ki bu ikisi birbirine ancak tek bir durumda eşit olabilir. Bu durum ise ikisinin de bir sabite eşit olması durumudur. Bu özel sabite, ayrıştırma sabiti denir.
Bu sabiti gama (Γ) harfi ile ifade edelim. Öyleyse eşitliğin her iki tarafını aşağıdaki gibi ifade edebiliriz:
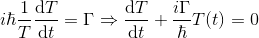
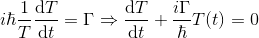
Bu da çözümü oldukça basit olan bir diferansiyel denklemdir. Çözümü:
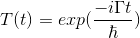
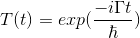
Aynı şekilde sağ tarafı da yazarsak:
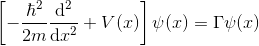
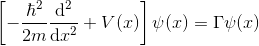
Bu denklemden gelecek çözüm de bizim dalga fonksiyonumuzu yani ψ(x)’i oluşturacak. T(t) ve ψ(x)’i değişken değiştirme metodunun başında oluşturduğumuz eşitliğe geri koyarsak:
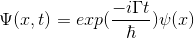
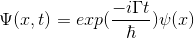
Gamanın Anlamı
Bu denklemin üzerine biraz düşünecek olursanız, zamana bağlı olarak salınım yapacağını görebilirsiniz. Bu salınımın frekansı aşağıdaki gibi ifade edilir.
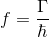
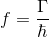
Planck’ın (ya da Einstein’ın) meşhur formulünü hatırlayalım.
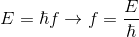
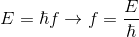
Bir benzerlik gördünüz mü? Evet! Bizim güzeller güzeli gamamız aslında enerji anlamına geliyor. Öyleyse son kez, zamandan bağımsız Schrödinger denklemini tekrar yazalım:
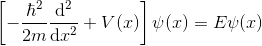
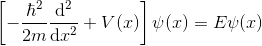
Dalga denkleminin küresel koordinatlarda nasıl çözüldüğünü merak ediyorsanız. bu çözümün yapıldığı yazımıza bakabilirsiniz.
Hazırlayan: Ege Can KARANFİL
Referanslar
1. David J. Griffiths, Introduction to Quantum Mechanics, 2nd edition
2. Prof. Dr. Gürsevil TURAN, Quantum Physics ders notları
Kapak Görseli
1. https://online.stanford.edu/courses/soe-yeeqmse01-quantum-mechanics-scientists-and-engineers
