Yıldız Astrofiziği: Virial Teoremi

- Özgün
Virial teoremi; kendi kütle çekimi altında çökerek, homojen kütle dağılımına sahip küresel bir yapı şeklinde dengeye gelmiş bir cismin, toplam kinetik enerjisinin, kütle çekimsel enerjisinin yarısına eşit olacağını ifade eder. Daha basit bir ifadeyle; hidrostatik dengedeki bir yıldızın, kütle çekimsel enerjisinin yarısı, gazı ısıtmak üzere termal enerji olarak harcanır.
U termal enerji, Ω kütle çekimsel potansiyel enerji olmak üzere, aşağıdaki şekilde ifade edilebilir.
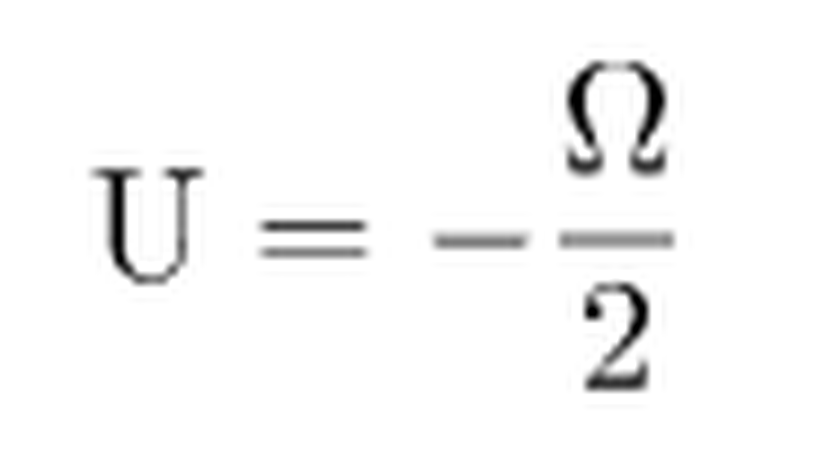
Eğer yıldız hidrostatik denge durumunda değilse, bu durumda bir eşitlikten söz edilemez. Kütle çekimsel enerjinin fazla olması durumunda, yıldız çökmeye devam edecek, bu süreçte de dengeye gelene kadar gazı ısıtmaya devam edecektir. (Ayrıca bkz. Jeans Kriterleri)
Virial Teoremi Denkleminin Elde Edilişi
Hidrostatik denge durumundaki bir yıldız için,
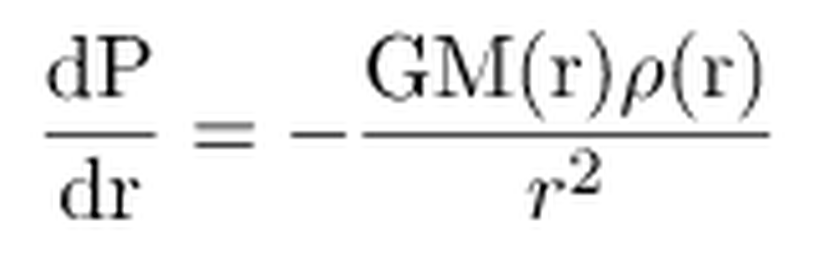
Bu denklemi
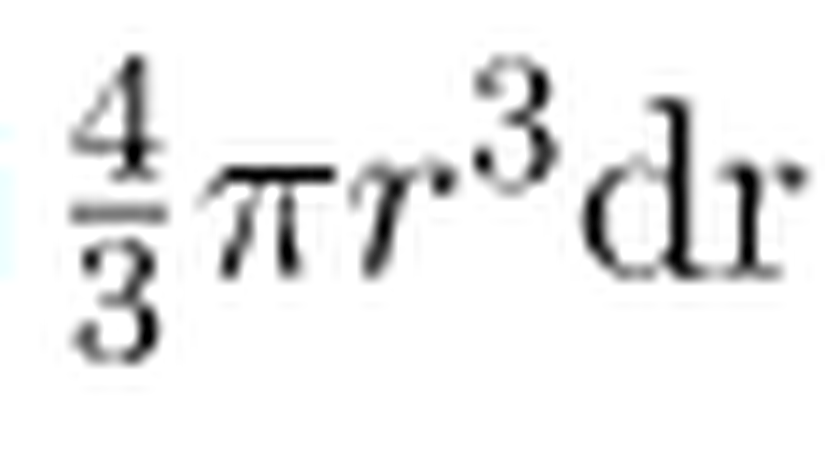
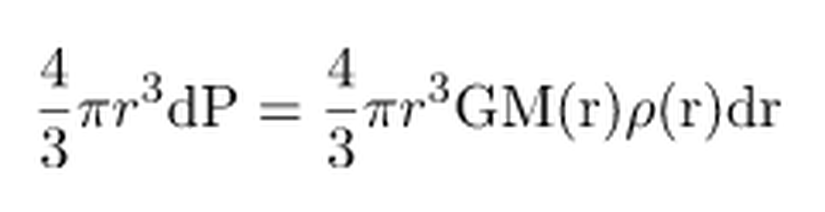
elde edilir. Birim kütle elemanı dM, birim alan ile yoğunluğun çarpımı olarak ifade edilebildiğinden,
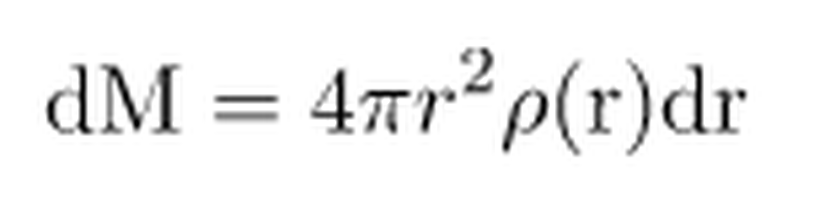
şeklinde yazılabilir. İlgili katmanın hacmi,
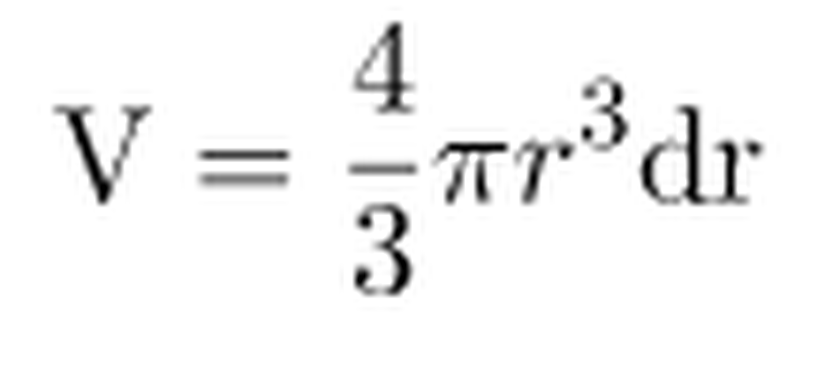
olduğuna göre, (4) numaralı denklem, (3) numaralı denklemde solundaki ifade yerine; (5) numaralı denklem ise (3) numaralı denklemde sağdaki ifade yerine yazılırsa, (3) numaralı denklem aşağıdaki şekle gelir.
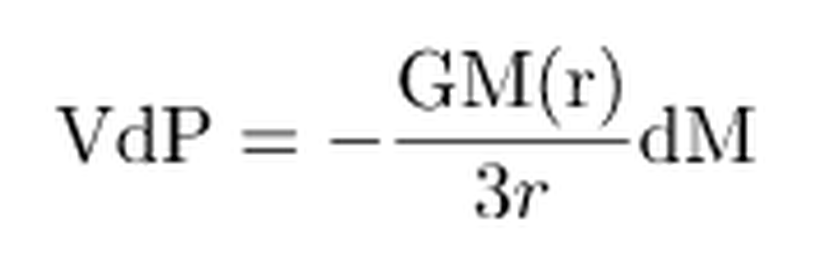
Eğer yıldızın kütlesi boyunca integral alırsak, kütle çekimsel potansiyel,
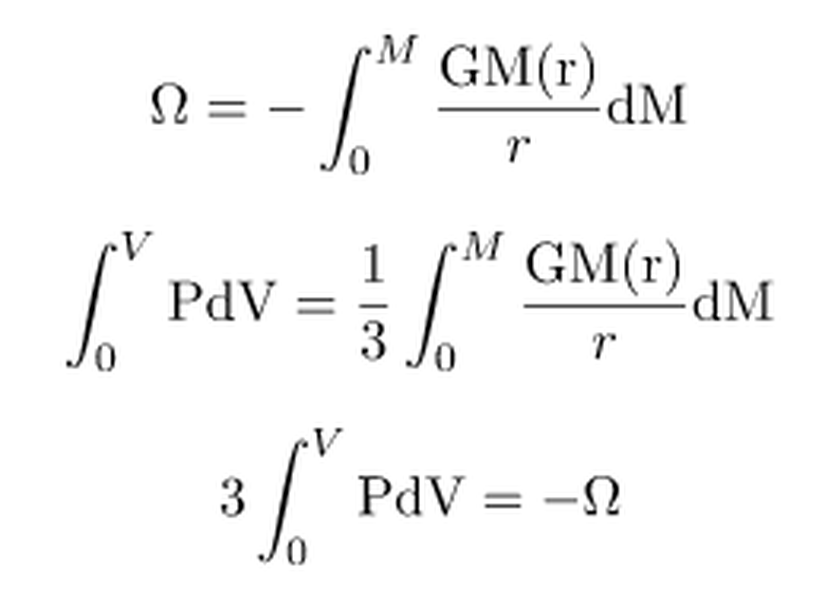
İdeal gaz yasasına göre, T sıcaklığına sahip bir gaz içerisindeki parçacıkların kinetik enerjileri 3kT/2'dir. Bu durumda termal enerji ϵ
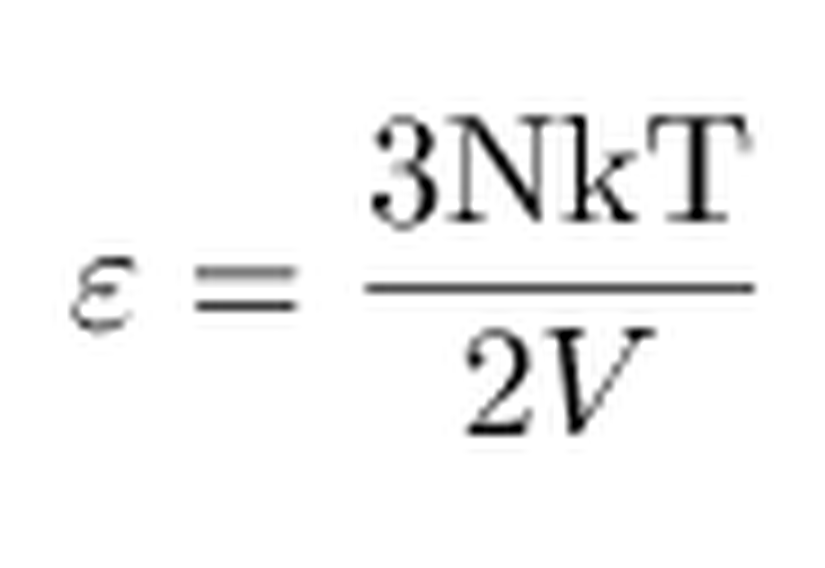
Gazlarda basınç için bildiğimiz PV=NkT ifadesini, ϵ cinsinden, P=2ϵ/3 olarak yazabiliriz. Bu durumda (9) numaralı ifade aşağıdaki şekilde yazılabilir.
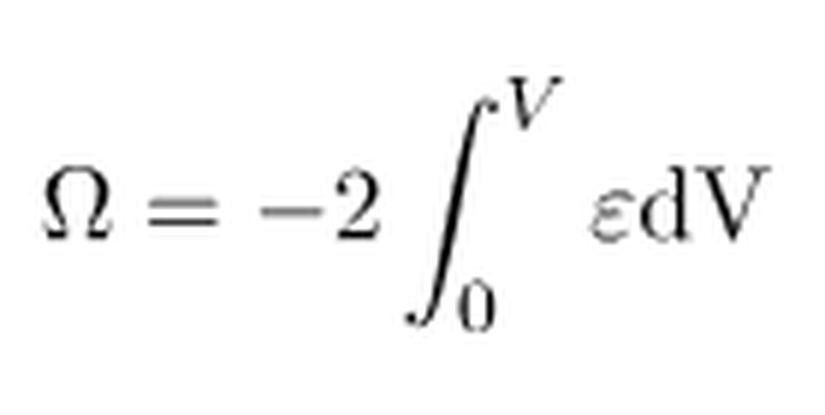
Bu ifadedeki integral kısmı yıldızın toplam termal enerjisi Uyu ifade eder. Böylelikle,
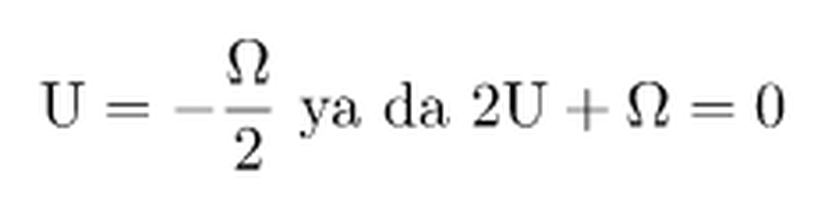
olarak bulunur.
Hazırlayan: Ögetay Kayalı
Kaynaklar
1. Melike Afşar, Solar System ders notları, Ege Üniversitesi Astronomi ve Uzay Bilimleri Bölümü
2. K.S.De Boer and W.Seggewiss, Stars and Stellar Evolution, 4.2.1 Virial Theorem, 57
3. The Virial Theorem, <http://hosting.astro.cornell.edu/academics/courses/astro201/vt.htm>
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 25/04/2024 15:46:50 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12886
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.



