Yıldız Astrofiziği: Jeans Kriterleri

- Özgün
Bir gaz kütlesinin çökmesi için yeterli koşul sınırını veren kriterlere,Jeans kriterleridiyoruz. Hidrostatik dengenin yokluğu, iki temel durumla açıklanabilir: Ya madde, kendi kütle çekimi üzerine çökmektedir ya da dağılmaktadır. Yıldız oluşumu sırasında, gaz kütlesi, kendi kütle çekimi altında çökmeye başlar. Bu çökmeye, içeride ısınan gazın oluşturduğu basınç karşı koyar. Kütle çöktükçe, basınç da artacağından bir noktada dengeye gelinir. Bu dengeye, hidrostatik denge denildiğini biliyoruz.
Tüm bu sınırlamaları bildiğimize göre, başlangıç koşulları belirlenen bir gaz kütlesinin, çöküp çökmeyeceğini de belirleyebiliriz. Jeans kriterlerini üç ayrı şekilde yazabiliriz: Jeans kütlesi, Jeans yarıçapı ve Jeans yoğunluğu.
Virial teoreminden bildiğimiz üzere, hidrostatik dengedeki bir ortam için -Ω=2U'dur. Fakat dengenin olmadığı, çökmenin gerçekleştiği durumları arıyorsak,-Ω>2U durumunu araştırmalıyız. Ω yani kütle çekimsel potansiyel enerji, termal enerji U'dan yeterince büyük olmalı ki sistem çökmeye başlayabilsin (ya da çökmeye devam edebilsin).
Jeans Kriterleri Denklemleri
Kütle çekimsel potansiyel enerji Ω aşağıdaki şekilde verilir.
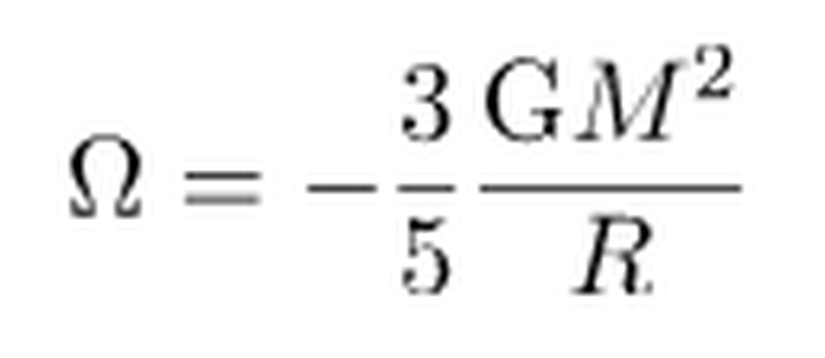
Termal enerji U ise,
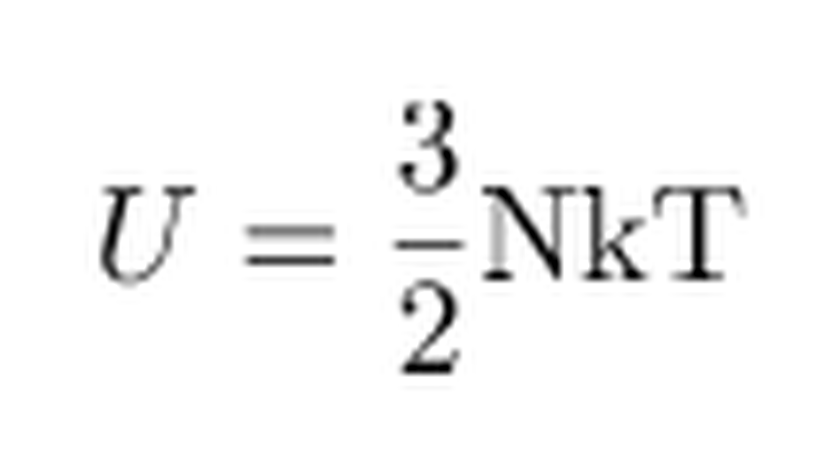
olarak verilir. Böylelikle bu iki ifadeyi, kütle çekimsel potansiyel enerjinin, termal enerjiden fazla olduğu koşulunda yerine yazacak olursak, aşağıdaki eşitsizliği elde ederiz.
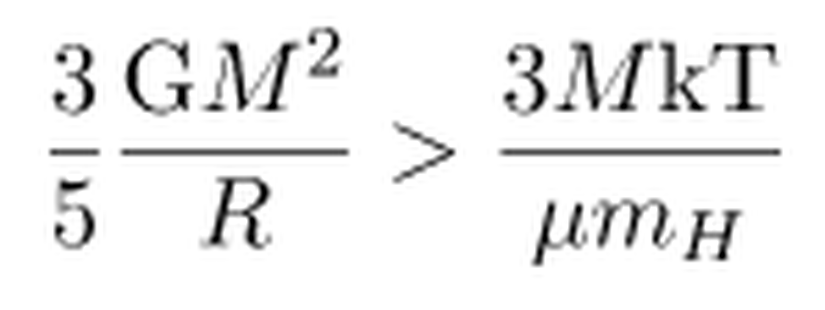
Jeans Kütlesi
Eşitsizlikteki R parametresini M cinsinden yazabiliriz. Küresel bir yapı için
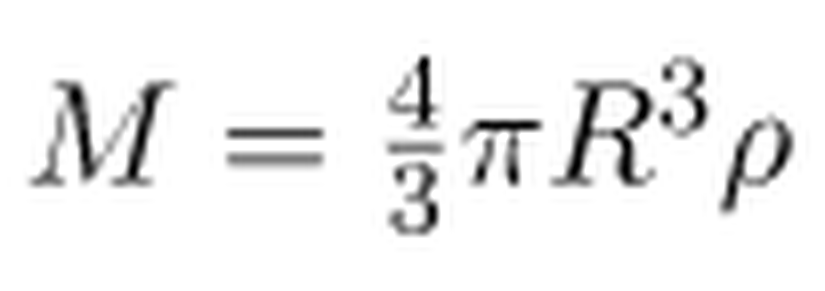
olduğuna göre,
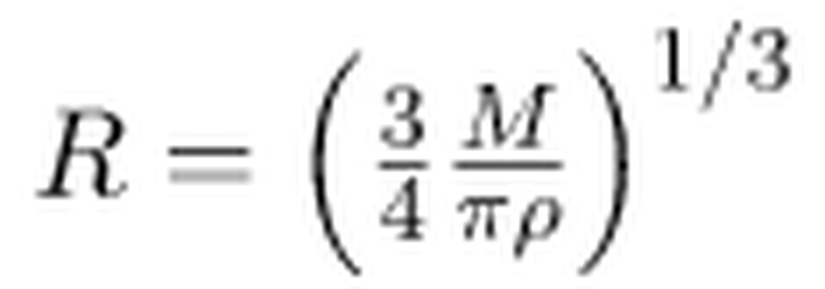
olarak yazılabilir. Eğer bu ifadeyi yerine koyacak olursak,
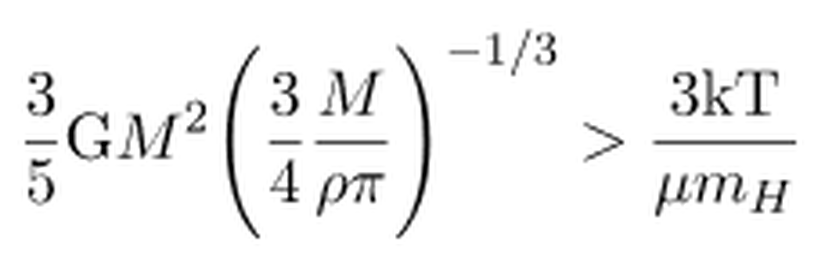
İfadeyi düzenlemek için M ifadesini kökün içerisinden çıkarıp, kalanları karşı tarafa attığımızda,
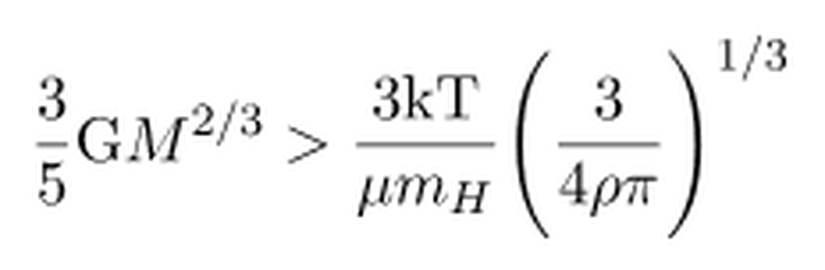
Eşitliğin bir tarafında kütle M ifadesini yalnız bırakalım.
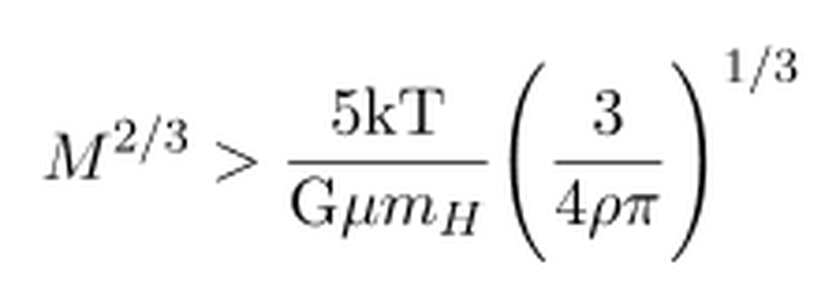
İfadenin üslerini düzenleyerek, kütle için sade bir hale getirirsek,
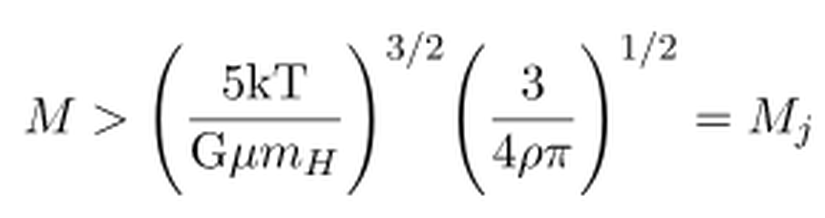
Böylelikle bulutsunun çökmesi için gerekli minimum kütle değeri olan Mj elde edilmiş olur.
Jeans Yarıçapı
(3) numaralı denkleme geri dönelim ve bu kez ifadeyi R cinsinden düzenleyelim.
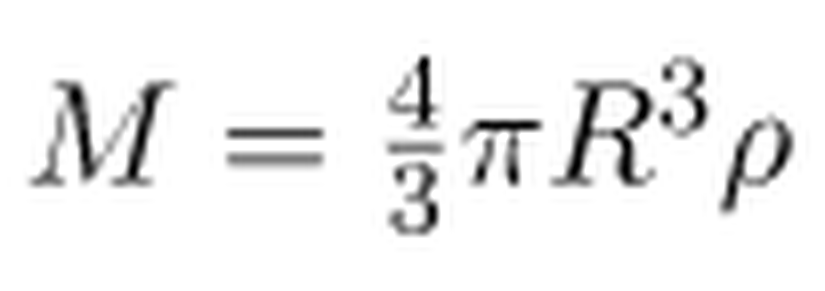
olduğuna göre, bu ifadeyi yerine yazacak olursak,
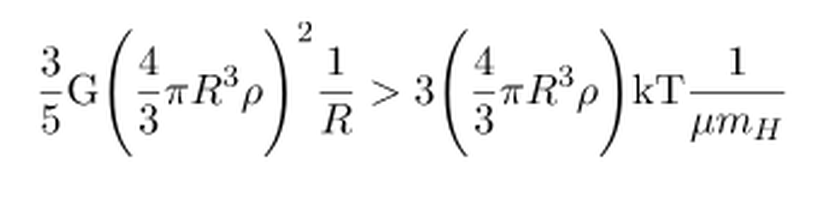
elde ederiz. Bu ifadede üsleri açıp, R ifadelerini sadeleştirdiğimizde denklem,
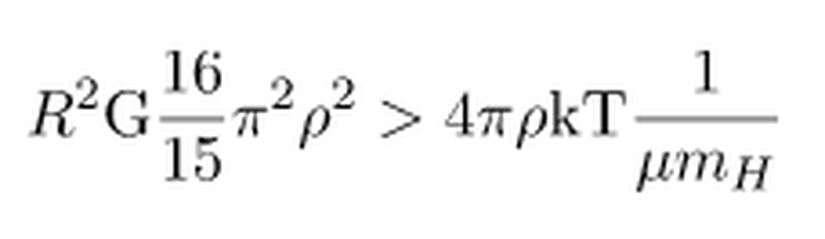
haline gelir. Eğer burada R2'yi yalnız bırakır ve her iki tarafın karekökünü alırsak, aradığımız R ifadesine ulaşırız.
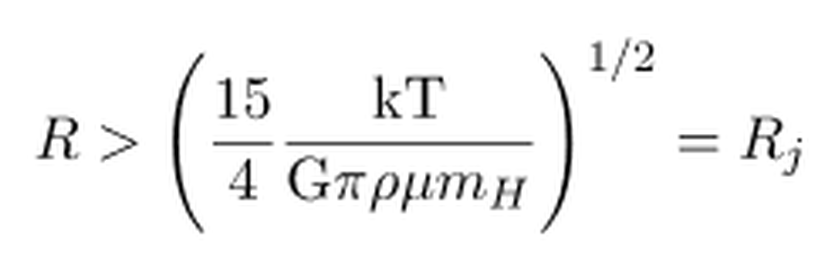
Böylelikle bulutsunun çökmesi için gerekli minimum yarıçap olan Rj bulunmuş olur.
Jeans Yoğunluğu
Jeans yoğunluğunu M'ye bağlı olarak yazmak için, (5) numaralı denkleme geri dönelim.
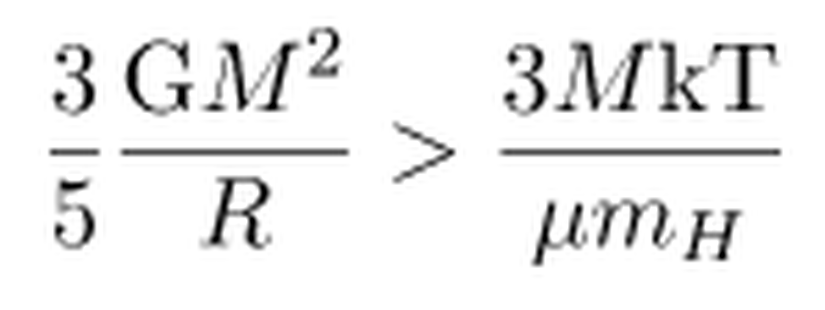
Eğer her iki tarafın karesini alarak;M2 ile ρ'nun yerini değiştirelim.
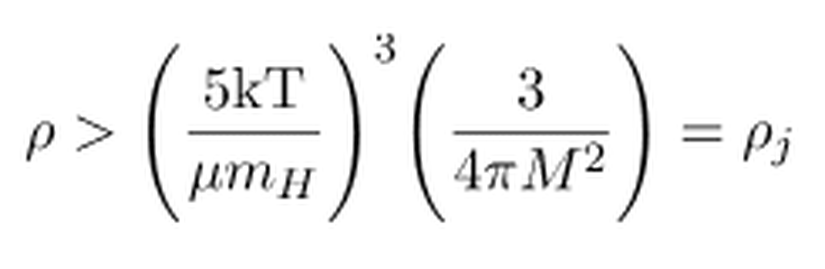
Böylelikle bulutsunun çökmesi için gerekli minimum yoğunluk değeri olan ρj elde edilir.
Hazırlayan:Ögetay Kayalı
Referanslar
1. Melike Afşar, Solar System ders notları, Ege Üniversitesi Astronomi ve Uzay Bilimleri Bölümü
2. K.S.De Boer and W.Seggewiss, Stars and Stellar Evolution, 7.3.1 Gravitational Instability (Jeans Instability), 106
3. Susanne Höfler, Gravitational Collapse, <https://www.astro.uu.se/~hoefner/astro/teach/apd_files/apd_collapse.pdf>
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 16/04/2024 10:54:25 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12911
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.




