Yıldız Astrofiziği – 5: Hidrostatik Denge

- Özgün
Hidrostatik denge aslında bir yıldızın (veya başka bir nesnenin) nasıl olup da stabil durduğunu açıklamamıza yardımcı olur. Yıldızlar, kendi kütle çekimleri altında çöken gaz ve toz bulutlarından oluşur. Bulut çökmesine devam ettiği sürece, daha küçük bir hacimde sıkışmaya başlayan gazın basıncı artar. Öyle bir noktaya gelinir ki, en sonunda basınç kuvveti, kütle çekim kuvvetine eşit olarak, gazın daha fazla kendi üzerine çökmesini engeller. Kütle çekim kuvveti ile basınç kuvvetinin dengelendiği bu duruma, hidrostatik denge denir (birçok öğrenci bunu basınç ile kütle çekim kuvvetinin dengelenmesi olarak ifade eder, fakat basınç kuvveti ile basınç farklı kavramlardır). Boşlukta bu kuvvetler dengesini sağlayan simetri bir küre olduğundan, yıldızlar küresel bir yapıya sahiptir. (Bkz. Kusursuz Küre)
Bulut kendi üzerine çöktüğü esnada, kaybettiği kütle çekimsel potansiyel enerjinin bir kısmını, termal (ısısal) enerjiye dönüştürür (Bkz. Virial Teoremi). Bu da, bulutun çöktükçe ısınmaya başlaması anlamına gelir. Bir noktada dengeye gelecek olan bu bulut, eğer nükleer tepkimeleri başlatacak yeterli sıcaklığa ulaşamadan hidrostatik dengeye gelirse, bir yıldız oluşmaz. Bu durumda bir taş yığını, gezegen ya da kahverengi cüce oluşturabilir.
Gezegenler, hatta atmosferimiz de hidrostatik denge halindedir. Atmosferi Dünya'nın yüzeyine yapışmaktan alıkoyan şey, kütle çekimi altında çökmeye çalışan gazın, aksi yönde oluşturduğu basınç kuvvetidir. Burada konuyu yıldızlar özelinde işliyor olsak da, atmosfer örneğinden de gördüğünüz üzere, hidrostatik denge daha genel bir kavramdır.
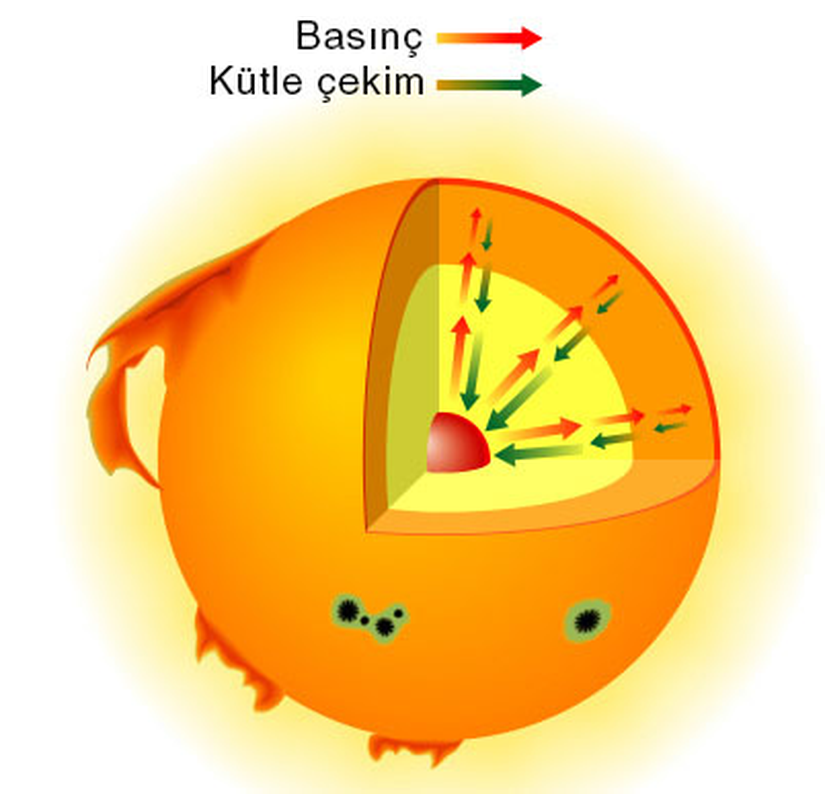
Hidrostatik Dengeye Etki Eden Faktörler
Aslında hidrostatik dengeye geldikten sonra bir yıldız her ne kadar belirli bir yarıçapa oturmuş olsa da, bu kuvvetler ortadan kalkmamıştır. Söz konusu kuvvetler hala oradadır, fakat birbirlerini dengelemektedir. İç yapıda meydana gelebilecek olası değişiklikler, bu kuvvet dengesinin bozulmasına neden olabilir. Örneğin bazı yıldızlar, belirli periyotlarla şişip büzülmektedir (bunlara zonklayan yıldızlar denir). Bu durum, basınçta meydana gelen ani değişikliklerin, kuvvetler dengesini belirli bir süreliğine bozmasından kaynaklanır.
Benzeri bir şekilde, eğer yıldız kendi ekseni etrafında çok hızlı dönüyorsa, özellikle ekvator bölgelerinde merkezkaç etkisi fazlaca hissedileceğinden, yıldız ekvator düzleminden dışa doğru şişerek küresel yapısını kaybedecektir. Güneş, oldukça yavaş dönen bir yıldız olduğu için bu durumdan etkilenmez, dönüş hızı saniyede 2 kilometre kadardır. Fakat VFTS 102 gibi bazı yıldızlar, saniyede 500 kilometre gibi muazzam dönüş hızlarına sahip olabiliyor. Böyle bir durumda yıldızın küresel yapısı ekvator düzleminden bozulmaya başlar. Dolayısıyla hidrostatik denge denklemine üçüncü bir parametre eklenmek zorundadır. Fakat Güneş gibi düşük hızlarda dönen yıldızlarda bu etki ihmal edilebilir düzeyde kalır. Fakat ihmal edilebilir düzeyde de olsa bu durum ekvator çapıyla kutup çapının bir nebze farklı olması üzerinde etkilidir.
Hidrostatik Denge Denklemi
Kuvvetler dengesini incelemek için, yapılabilecek birçok yaklaşım bulunuyor. Bunlardan birisi yıldızın herhangi bir katmanı üzerinde bir hacim elemanı alıp, bu hacim elemanın taban ve tavan yüzeylerine uygulanan basınç kuvvetleri ile kütle çekim kuvvetlerini eşitlemektir. Ardından çıkan ifadeler sadeleştirilerek hidrostatik denge denklemine ulaşılabilir. Fakat daha basit bir yaklaşımla da olayı çözebiliriz.
Yine benzer bir şekilde dV hacminde ve dA yüzey alanına sahip bir hacim elemanı düşünelim. Kalınlığı dr, merkezden uzaklığı da r olsun. Bu durumda bu elemana uygulanan kütle çekim kuvveti,
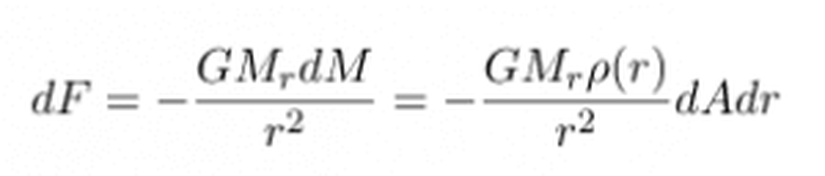
olur. Burada dM, dV hacmindeki kütle, Mr ise r'ye bağlı kütledir.
Bu noktadan sonra çözümümüzü basitleştiren varsayım ise şudur: Toplam net kuvvetin sıfırlanması için (dengede olması için) gerekli koşul, ancak basınç kuvvetindeki değişimin, kütle çekim kuvvetine eşit olmasıyla gerçekleşir. Yani bu durumda dP=dF/dA. Böylelikle yukarıdaki denklemi dA'ya bölersek dP'yi elde ederiz, ardından dr'ye bölerek sonuç,
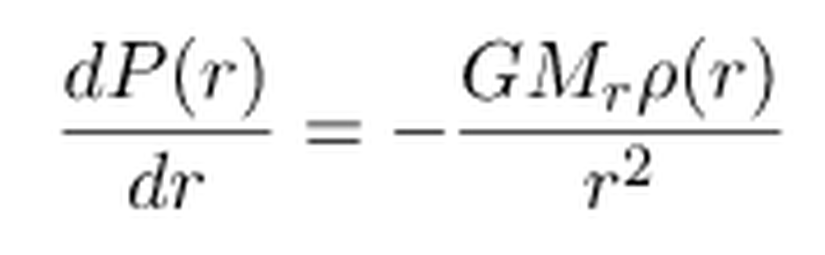
olarak elde edilir. Bu denklem, hidrostatik denge denklemi olarak bilinir. Sadece yıldız oluşumunda ve dinamiklerini açıklamakta önemli bir yer edinmez, hayatımızın birçok noktasında da karşımıza çıkar.
Hazırlayan: Ögetay Kayalı
Referanslar
1. K. S. De Boer and W. Seggewiss, Stars and Stellar Evolution, Chapter 4, Stellar Structure: Basic Equations, p.53
2. Dengkai Jiang et al, "The binary merger channel for the progenitor of the fastest rotating O-type star VFTS 102"
<http://mnras.oxfordjournals.org/content/428/2/1218.short>
Görseller
Figür 1. <https://ryanoursun.wikispaces.com/What+is+Hydrostatic+and+Thermal+Equilibrium%3F_jake>
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 19/04/2024 02:07:50 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12860
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.


