Yamuk nedir? Formülleri ve Özellikleri

- Özgün
Yamuk, yalnızca iki kenarı paralel olan dörtgendir ve paralel kenarlarının uzunlukları her zaman birbirinden farklıdır. Paralel olmayan diğer iki kenarının ise uzunlukları eşit olabileceği gibi olmayabilir de. Eşit olduğu durumlarda bu yamuğa, ikizkenar yamuk adı verilir.
Elbette tek özel yamuk, ikizkenar yamuk değildir. Bunun dışında bir kenarı, iki paralel kenara dik olan yamuğu, dik yamuk olarak adlandırırız. Aşağıdaki görselde yamuk türlerine örnekler görebilirsiniz.
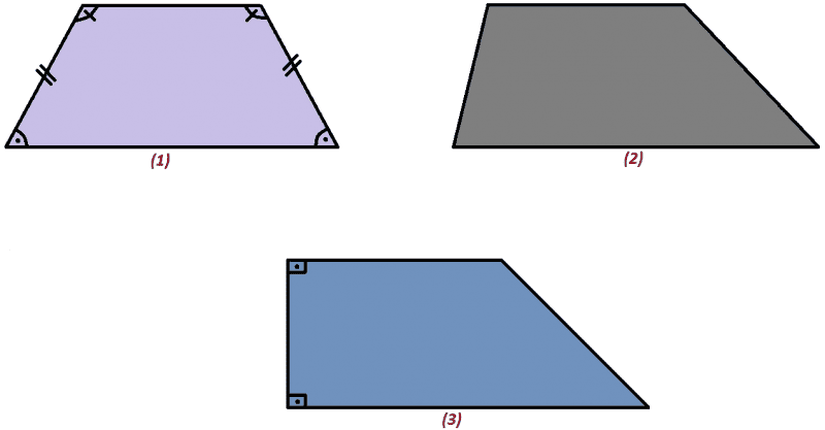
Tüm dörtgenlerde olduğu gibi, yamuğun da iç açıları toplamı 360°'dir (Öklidyen uzayda). Bununla birlikte, ikizkenar ve dik yamuk hariç, tüm iç açıları birbirinden farklıdır. Tabii her açının birbirinden farklı olması rastgele oldukları anlamına gelmez. Türü fark etmeksizin, karşılıklı paralel kenarlardan olan açılar için, iki açının toplamı daima 180°'dir. Yani a+d ve b+c daima 180° olur. Bu durum, tanımından da anlaşılacağı üzere paralelliğin doğurduğu bir sonuçtur, neden böyle olduğunu düşünmeyi size bırakıyoruz.
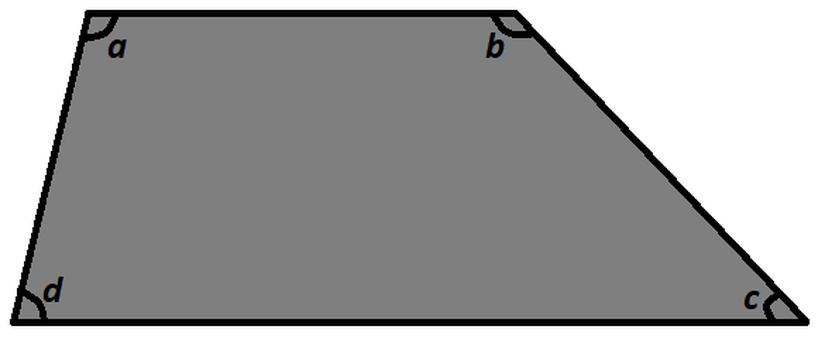
Bahsettiğimiz üzere şekilde gösterilen yamukta a + d = b + c = 180° olur. Bu bağıntı U kuralı diye adlandırdığımız, geometride kullanılan bir kuraldan gelir. Bu kurala göre iki paralel doğruyu birleştiren üçüncü bir doğru parçasıyla bu doğrular arasında kalan açılar birbirinin bütünleridir; yani toplamları 180°'yi verir.
Yamuğun Özellikleri
1. Köşegenler
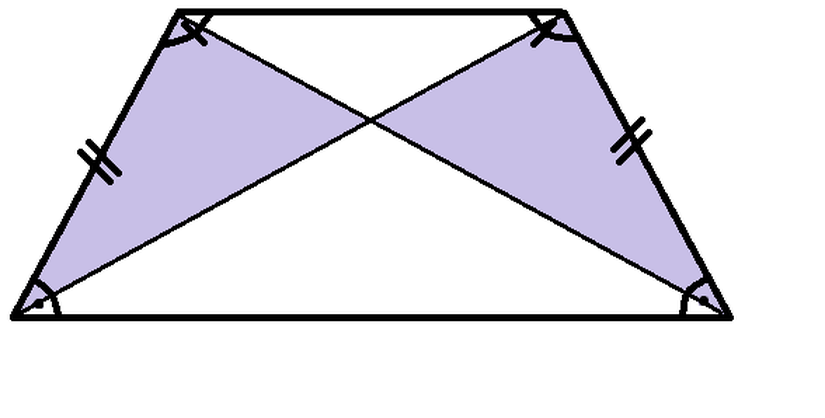
Köşegen, bir geometrik şekilde komşu olmayan iki köşeyi birbirine bağlayan doğru parçasına verilen addır. Yamukta, ikizkenar yamuk hariç, köşegen uzunlukları birbirinden farklıdır. İkizkenar yamuğun ise iki köşegeninin de uzunlukları birbirine eşittir. Bu nedenle ikizkenar yamuğun köşegenlerinin yamuğu böldüğü dört parçadan ikisinin alanı birbirine eşittir. Birbirine eşit olan bu alanlar aşağıdaki görselde renkli gösterilen kısımlardır.
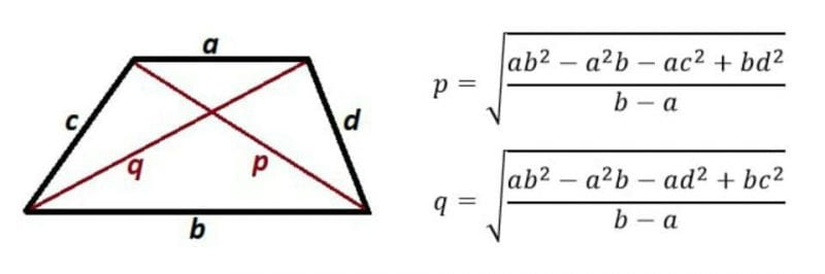
İster ikizkenar olsun ister olmasın herhangi bir yamuğun kenar uzunlukları bilindiğinde iki köşegeninin de uzunluklarını hesaplamak mümkündür. Bunun için aşağıda gösterilen bağıntılar kullanılır.
2. Alan
Yamukta alan bulabilmek için tabanların uzunluğuna ve yüksekliğine ihtiyacımız vardır. Taban olarak adlandırdığımız yer yamuğun paralel kenarları, yükseklik ise bu iki kenar arasındaki en kısa uzaklıktır. Paralel olmayan diğer iki kenar ise bacak olarak adlandırılır.
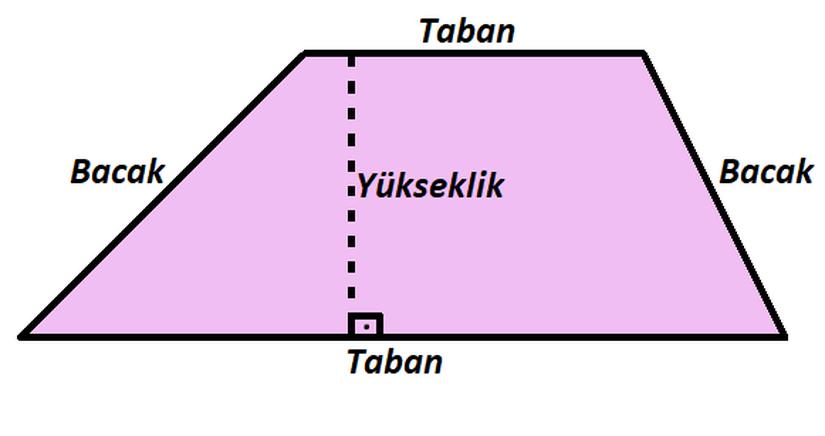
Taban ve yükseklik bilgilerine sahip olduğumuzda yamuğun alanını aşağıdaki şekilde hesaplarız.
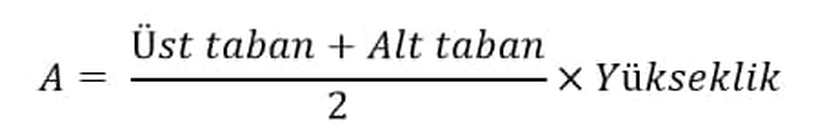
Bu denklemin ne anlattığını anlamak önemlidir. Üst taban artı alt taban bölü iki neyi ifade eder? Sanki yükseklikle bunu çarparken bir dikdörtgenin alanını hesaplıyormuşuz gibi görünmektedir. Bu ifade aslında iki terimin toplamının ikiye bölümünden, bir ortalamayı andırmaktadır. Aşağıdaki medyan özelliğinden bunun ne anlam ifade ettiğini anlayabiliriz.
3. Medyan Özelliği
Bir yamuğu, paralel kenarlarına eşit uzaklıkta ve yine bunlara paralel bir doğru parçasıyla böldüğümüzde, bu doğru parçasının uzunluğu iki paralel kenarın uzunlukları ortalamasına eşit olur.
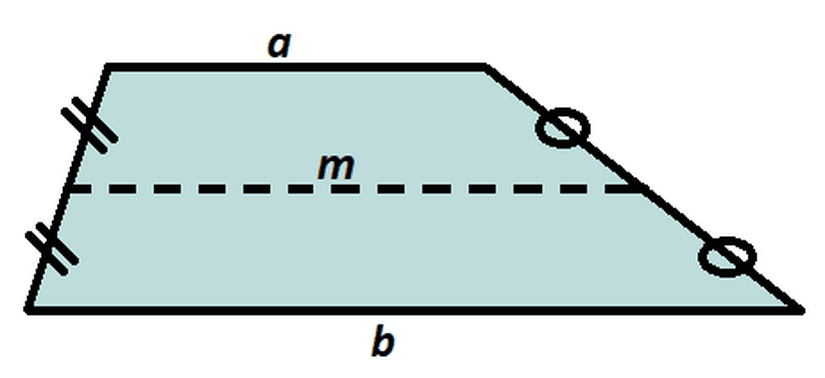
Ayrıca, bir önceki başlıkta bahsettiğimiz alan bulma yöntemine ek olarak yukarıdaki görselde m olarak adlandırılan medyanı kullanarak da yamuğun alanını hesaplamak mümkündür. Bu yöntem için yamuğun alt ve üst tabanlarının bilinmesine gerek yoktur, çünkü zaten medyanın uzunluğu, iki tabanın toplamının yarısı, yani ortalaması kadardır.
Bu durumda yamuğun alanını A, yüksekliğih olarak tanımlarsak,
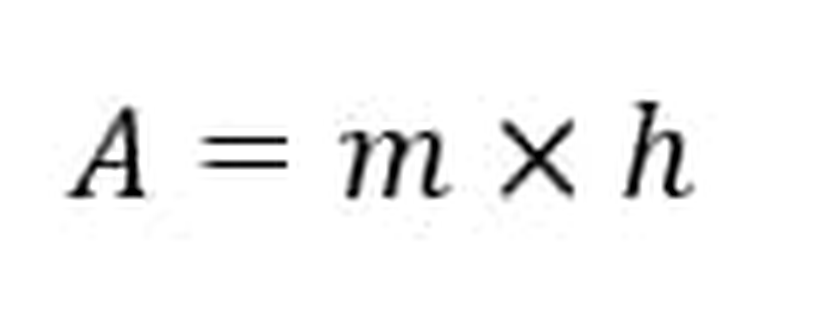
olduğunu görürüz. Aslında yamukta alan bulma bu kadar kolaydır. Fakat bu denklemlerin nereden geldiği hemen göze çarpmayabilir. Bunun için çeşitli senaryoları deneyerek, tutarlılıkları test etmenizi öneriyoruz. Örneğin bir ikizkenar yamuğun alanı gerçekten burada tanımlandığı gibi midir? Bunu kontrol etmek kolaydır, çünkü onu bir dikdörtgene ve bir üçgene ayırarak ayrı ayrı alanlarına bakabiliriz. Bu durumda toplamın, gerçekten de buna eşit olduğu görülür.
Bu gibi yaklaşımlar yaparak bu denklemlerin nasıl ortaya çıktıklarını anlamak oldukça önemlidir. Çünkü tek başlarına bakıp anlamaya çalıştığınızda, ilk bakışta hiçbir anlam ifade etmeyebilirler. Lakin nasıl ortaya çıktıklarını anlar ve çeşitli yollardan gerçekten böyle olduğunu kendiniz görürseniz, bu formülleri kolay kolay unutmazsınız.
Bu tür temel konuları ezberlememeli ve daima "nasıl" böyle olduklarını sorgulamalısınız. Ancak bu sayede konunun özünü anlayabilir ve sorunsuz bir öğrenme sürecinden geçebilirsiniz. Yoksa sürekli olarak unutur, bir süre sonra baskı ve stres altında rahatsız olmaya başlarsınız. İlk etapta yorucu gibi görünen bu sorgulamalar, uzun vadede size daima kazandıracaktır!
Hazırlayan:Arya Elçi
Editör:Ögetay Kayalı
Referanslar:
1.Math is Fun, "Trapezoid", < https://www.mathsisfun.com/geometry/trapezoid.html >
2.Wolfram Math World, "Trapezoid", < https://mathworld.wolfram.com/Trapezoid.html >
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 25/04/2024 04:12:38 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12840
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.




