Vektör Nedir? Skaler Çarpım ve Vektörel Çarpım Arasında Ne Fark Var?

- Özgün
- Fizik
Skaler ve vektörel kavramlarını tanımlarken de ifade ettiğimiz gibi fizikte yalnızca sayılara değil, aynı zamanda onlara fiziksel anlam katan niceliklere de bakarız. Sıcaklık gibi skaler bir niceliği 32°C ile ifade ederken, hız gibi vektörel bir niceliğe ise 50 km/sa demenin yanında bir de ek olarak yön belirterek kullanırız. Yani vektörler, hem büyüklükleri hem de yönleri olan fiziksel nicelikleri ifade etmek için kullandığımız bir araçtır.
Bu yazıda iki farklı çarpma tanımını göreceksiniz ve bu, muhtemelen size biraz tuhaf gelecek. Örneğin şu zamana kadar "A çarpı B" ile "B çarpı A"'nın aynı sonucu verdiğini bir mutlak gibi kafanıza yerleştirdiniz; fakat vektör matematiğinde bu, biraz daha farklı bir anlam ifade eder ve her zaman doğru olmayabilir. Bu nedenle skaler çarpım ve vektörel çarpım konularındaki bazı tanımlar size tuhaf gelebilir, neden böyle şeylerden bahsediliyor diye düşünebilirsiniz. Lakin bunun nedenlerini konuya girdikçe daha iyi anlayacaksınız. Bu ayrımı anlamak oldukça elzemdir.
Koordinat Sistemleri
Yön kavramı işin içerisine dahil olduğundan, iyi tanımlamalar yapabilmek için koordinat sistemlerine ihtiyacımız var. Hiç kuşkusuz ilk akla gelen kartezyen koordinat sistemleridir. Burada bir noktayı, karşılık geldiği x ve y değerleri ile (x,y)\text{(x,y)} şeklinde ifade ederiz.
Fakat her ne kadar göze çok basit görünse de fizikte kartezyen koordinatları seçmek çoğunlukla baş ağrıtır. Onun yerine, yaptığımız bir takım fiziksel işlemleri kolaylaştıran temellere sahip kutupsal koordinat sistemlerini kullanacağız. Elbette durumdan duruma, bunları değiştirmenizde ya da birbiri arasında dönüştürmenizde bir sakınca yoktur.
Kutupsal koordinat sisteminde, orijinden ilgili noktaya olan uzaklık r ile gösterilir. Genellikle de pozitif x-ekseninden saat yönünün tersinde ölçülen θ\text{θ} ("teta") açısı buna eşlik eder. Dolayısıyla kutupsal koordinatlarda (r,θ)\text{(r,θ)} gösterimine sahip oluruz. Elbette kartezyen koordinatlar olan (x,y)\text{(x,y)}'den, kutupsal koordinatlar olan (r,θ)\text{(r,θ)}'ya dönüşüm yapabiliriz.
x=rcosθy=rsinθ\Large x=r\cos{\theta} \newline y=r\sin{\theta}
Bu eşitlik hiç kuşkusuz trigonometrinin en temel tanımlarından gelmektedir. Bunları kolaylıkla bulabileceğiniz için, en azından bir kere kendinizin bulmasını tavsiye etmek durumundayız.
Keza θ\text{θ} açısının tanjant değeri de aşağıdaki gibi ifade edilir.
tanθ=y/x\Large \tan{\theta}=y/x
Pisagor bağıntısından yola çıkarak ilgili r\text{r} değerimizi de aşağıdaki gibi tanımlarız:
r=x2+y2\Large r=\sqrt{x^2+y^2}
Vektör Nedir?
Vektör, büyüklüğü (ya da uzunluğu) ve yönü olan geometrik bir niceliktir. Kimi zaman geometrik vektör, uzaysal vektör veya Öklidyen vektör de denilir. En basit tabiriyle, yön kavramı eklenmiş skaler nicelik gibi düşünebilirsiniz. Vektörleri ifade ederken, onları diğerlerinden ayırmak için genellikle iki temel yöntemden biri kullanılır. Örneğin bir A\text{A} vektörünü ifade etmek istiyorsak ya kalın harflerle A\bold{A} yazarız ya da A⃗\vec{A} şeklinde üzerinde bir ok işaretiyle gösteririz.
A\bold{A} vektörünün büyüklüğü ise A\text{A} olarak veya |A|\text{|A|} olarak yazılır. Örnek bir vektör gösterimi ise aşağıdaki gibidir.
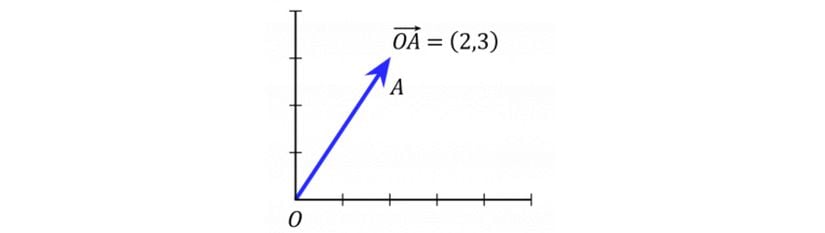
Genellikle böyle bir gösterimde OA vektörünü göstermek için üzerinde ok işaretli bir gösterim tercih etmeyiz (bu işleri uzatmaktan ve karışık hale getirmekten başka bir işe yaramaz). Bunun yerine bu vektöre herhangi bir harf veririz, örneğin a\bold{a} vektörü deriz ve aşağıdaki gibi tanımlarız.
a=(2,3)\Large \bold{a}=(2,3)
Vektörlerin Eşitliği
Eğer A\bold{A} ve B\bold{B} vektörü aynı büyüklüğe ve aynı yöne sahipse bu iki vektör eşit alınabilir. Bir başka deyişle paralel doğrular boyunca eşit büyüklüktelerse A=B\bold{A}=\bold{B} denilebilir. Aşağıdaki görsel bu durumu özetlemektedir.
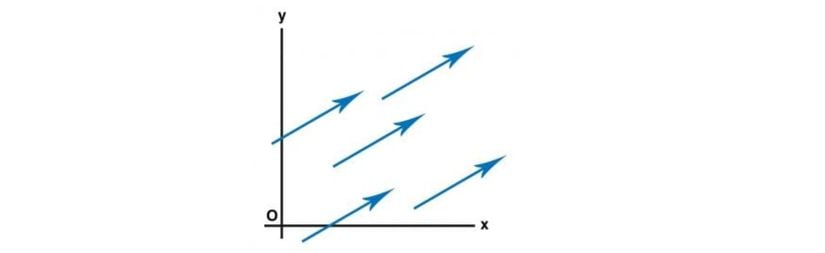
Bu durum bize vektörün büyüklüğünü ve yönünü değiştirmeden onu ötelememize olanak sağlar.
Vektörlerin Toplanması
Şu zamana kadar kullandığınız matematikte toplama ve çıkarma için özel incelemeler yapmanız gerekmediyse bu durumu biraz yadırgayabilirsiniz. Fakat vektörler, matematiğin özel bir alanı olduğundan ayrıca irdelenmeyi gerektirir. Bildiğimiz şekilde toplanıp çıkarılmadıklarından ya da çarpılıp bölünmediklerinden emin olmamız lazım.
Neyse ki vektörlerin toplanması ve çıkarılması o kadar sıkıntılı bir durum değildir. Üstelik hangi sırayla topladığımıza da dikkat etmemiz gerekmez. Yani:
A+B=B+A\Large \bold{A}+\bold{B}=\bold{B}+\bold{A}
olarak yazılabilir. Buna toplamanın komütatif olması denir. İlk defa böyle bir kavramlarla karşılaştıysanız, neden böyle olağan bir şeyi açıklığa kavuşturmaya çalıştığımız tuhaf gelebilir. Bu noktada şunu fark etmeniz gerekiyor, bu her zaman böyle olmak zorunda değildir. Fakat vektörlerde toplama, komütatiftir. Aynı zamanda;
(A+B)+C=A+(B+C)\Large (\bold{A}+\bold{B})+\bold{C}=\bold{A}+(\bold{B}+\bold{C})
olarak da yazılabilir. Buna birleştirilebilir (asosiye) olma durumu denir. Bir de dağılma özelliği vardır. O da;
α(A+B)=αA+αB\Large \alpha(\bold{A}+\bold{B})=\alpha \bold{A} + \alpha \bold{B}
şeklinde yazılır. Burada α \text{α }bir skalerdir. Bunu bir nevi vektörün önüne gelen bir katsayı olarak görebilirsiniz, hiç kuşkusuz etkisi vektörün büyüklüğünü artırmak ya da azaltmaktır, onun yönü üzerinde bir etkisi yoktur.
Bu noktada vektörlerde çıkarma işlemini ele almak gerek. Çıkarmayı yaparken, o vektörün ters işaretlisi ile toplamaya odaklanalım, aslında yaptığımız şey budur. Yani bir A\bold{A} vektöründen B\bold{B} vektörünü çıkarmak istiyorsak, B\bold{B}'nin yönünü ters çevirir ve A\bold{A} ile toplarız.
A−B=A+(−B)\Large \bold{A}-\bold{B}=\bold{A}+(-\bold{B})
Şu noktada, bütün bu yazdıklarımızı biraz görselleştirmeye ihtiyacımız var. En nihayetinde vektörler geometrik bir anlam taşıyor. Bunun için paralelkenar yöntemi adını verdiğimiz oldukça sıradan bir yöntem kullanırız. A\bold{A} ve B\bold{B} vektörleri aşağıda oldukları gibi uç uca eklenir. A+B\bold{A}+\bold{B} toplamından elde edilen vektör ise başlangıç noktasından, bitiş noktasına çizilen vektör olur. Burada komütatifliği de doğrudan görebilirsiniz, paralelkenarın bir tarafı bir işlemi, diğer tarafı öbür işlemi tanımlar fakat sonuç aynıdır.
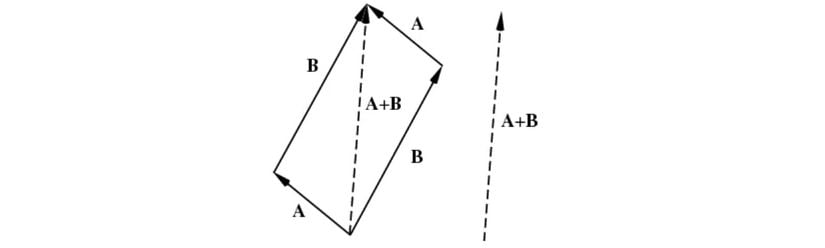
Skaler Çarpım (Nokta Çarpım)
Vektörlerde çarpım, toplama kadar sıradan değildir. Vektörlerle yapacağımız iki farklı türden çarpım söz konusudur. Bunlar skaler çarpım ve vektörel çarpımdır.
Skaler çarpım, nokta ile gösterildiği için "nokta çarpım" olarak da bilinir (vektörel çarpımda ise daha klasik olan ""çarpı işareti" kullanılır) ve aşağıdaki gibi tanımlanır:
A⋅B≡ABcosθ\Large \bold{A} \cdot \bold{B}\equiv AB\cos{\theta}
Buradaki teta açısı (θ\text{θ}), A\bold{A} ve B\bold{B} vektörü arasındaki açıdır. Geometrik olarak bu çarpım, A defa B\bold{B}'nin A\bold{A} boyunca olan izdüşüm çarpımından ibarettir. Bu yorumu anlamak için paralel ve dik olma durumlarını ele alabilirsiniz. Paralel olması durumunda kosinüs ifadesi birdir ve çarpım bu iki vektörün büyüklükleri çarpımından ibaret olur. Dik oldukları durumunda ise sonuç sıfırdır, çünkü diğeri üzerine bir izdüşüm yoktur. Ayrıca bu çarpımın sonucunun bir skaler olduğuna dikkat edin, bu nedenle skaler çarpım olarak adlandırılır. Girdide iki vektör vardır, fakat sonuç bir skalerdir.
Skaler çarpımda da, toplamada olduğu gibi komütatiflik özelliği bulunur.
A⋅B=B⋅A\Large \bold{A} \cdot \bold{B} = \bold{B} \cdot \bold{A}
Ayrıca dağılma özelliğine de sahiptir.
A⋅(B+C)=A⋅B+A⋅C\Large \bold{A} \cdot (\bold{B}+\bold{C})=\bold{A} \cdot \bold{B}+\bold{A} \cdot \bold{C}
Sadece bu iki özelliği kullanarak kosinüs yasasını ispatlamak oldukça kolaydır. C=A-B\text{C=A-B} gibi bir vektör tanımlar ve C⋅CC\cdot C skaler çarpımına bakacak olursanız:
C⋅C=(A−B)⋅(A−B)=A⋅A−A⋅B−B⋅A+B⋅B\bold{C}\cdot \bold{C}=(\bold{A}-\bold{B})\cdot (\bold{A}-\bold{B})=\bold{A}\cdot \bold{A} - \bold{A} \cdot \bold{B} - \bold{B} \cdot \bold{A} + \bold{B} \cdot \bold{B}
olduğunu bulursunuz. Bunu düzenlediğimizde ise aşağıdaki gibi kosinüs teoremini elde ederiz.
C2=A2+B2−2ABC^2=A^2+B^2-2AB
Vektörel Çarpım (Çapraz Çarpım)
Bir diğer çarpım olan vektörel çarpımı ise çarpı işareti olan "x" işaretiyle gösteririz (skaler çarpımda bu noktaydı). A\bold{A} ve B\bold{B}'nin vektörel çarpımı ise aşağıdaki gibi tanımlanır.
A×B≡ABsinθn^\Large \bold{A} \times \bold{B}\equiv AB\sin{\theta}\hat{\bold{n}}
Burada ilk dikkat edilmesi gereken bu çarpımın sonucunun da bir vektör olduğudur, skaler çarpımda sonuç bir skalerdi. Bunu da buradaki n^\hat{\bold{n}} ("şapkalı n") vektörü sağlar. Bu, A\text{A} ve B\text{B} düzleminden dik yönelmiş bir birim vektördür. Fakat bu düzleme dik iki ayrı yön söz konusudur. Bu durumu açıklığa kavuşturmak için sağ el kuralı kullanılır. Eğer parmağınızı herhangi bir vektör yönünde doğrultur ve ardından diğer vektörün olduğu yöne doğru bükerseniz, baş parmağınız çarpımın sonucunun yönünü gösterecektir.

Örneğin yukarıdaki görseli inceleyelim. İşaret parmağınızı u yönünde tutun ve v'ye doğru kıvırın. Bu durumda baş parmak, çarpımın olduğu yön olan yukarıyı işaret eder. Tersini yapmaya kalkar ve v yönünde seçerseniz, tam olarak güzel bir özelliği keşfedersiniz. Bu durumda baş parmak aşağıyı gösterecektir. Bu şunu ifade eder:
B×A=−(A×B)\Large \bold{B}\times \bold{A} = -(\bold{A}\times \bold{B})
Yani vektörel çarpım komütatif değildir. Fakat dağılma özelliğini gösterir.
A×(B+C)=(A×B)+(A×C)\Large \bold{A} \times (\bold{B}+\bold{C})=(\bold{A} \times \bold{B}) + (\bold{A} \times \bold{C})
Ayrıca ∣A×B∣|\bold{A} \times \bold{B}| ifadesi A\bold{A} ile B\bold{B} tarafından oluşturulan paralelkenarın alanını ifade eder. Bu nedenle bu iki vektör paralelse, sonuç sıfırdır (sinüs ifadesinden dolayı).
Vektör Bileşenleri
Herhangi keyfi bir A vektörü alırsak, bunu baz vektörlerini kullanarak aşağıdaki gibi ifade edebiliriz.
A=Axx^+Ayy^+ Azz^\Large \bold{A}=A_x \hat{\bold{x}} + A_y \hat{\bold{y}} + A_z \hat{\bold{z}}
Burada x^\hat{\bold{x}}, y^\hat{\bold{y}} ve z^\hat{\bold{z}} ifadeleri kartezyen koordinatlardaki üç baz vektörüdür. Bu birim vektörlerin, önlerine gelen ilgili eksenin katsayısıyla çarpıldığında, o eksendeki bileşenini ifade eden vektörü vereceklerdir. Bu üç eksendeki bileşenler de uç uca eklenip toplanınca, ilgili vektörün kendisini verecektir. Böylelikle bir vektör, bileşenlerine ayrılmış olur. Burada kolaylık açısından koordinat sistemimizi, kartezyen koordinatlar olarak seçtik. Şu durumda hani kartezyen koordinatlar bize zorluk çıkarıyordu diye düşünebilirsiniz. Fakat amacımız sadece tanımlamalar yapmak, durumu işlemlere girdiğinizde daha iyi kavrayacaksınız.
Bu durumda iki vektör, bileşenleri göz önüne alındığında aşağıdaki gibi toplanır.
A+B=(Axx^+Ayy^+Azz^)+(Bxx^+Byy^+Bzz^)=(Ax+Bx)x^+(Ay+By)y^+(Az+Bz)z^\large \bold{A} + \bold{B} = (A_x \hat{\bold{x}} + A_y \hat{\bold{y}} + A_z \hat{\bold{z}}) + (B_x \hat{\bold{x}} + B_y \hat{\bold{y}} +B_z \hat{\bold{z}}) \newline =(A_x+B_x)\hat{\bold{x}}+(A_y+B_y)\hat{\bold{y}}+(A_z+B_z)\hat{\bold{z}}
Bir skalerle çarpıldığında ise aşağıdaki durum gerçekleşir.
αA=(αAx)x^+(αAy)y^+(αAz)z^\Large \alpha\bold{A}=(\alpha A_x) \hat{\bold{x}} + (\alpha A_y) \hat{\bold{y}} + (\alpha A_z) \hat{\bold{z}}
Bu durum oldukça akla yatkındır. Çünkü bir vektörü skalerle çarpmak, onu belirli bir oranda küçültmek ya da büyütmek anlamına gelir. Bunun gerçekleşebilmesi için her bir bileşen aynı oranda değişmelidir.
Bir vektörün skalerle çarpımı onun doğrultusunu değiştirebilir. Vektörün doğrultusu işaretle belirlenir (+ veya -), dolayısıyla negatif bir skalerle çarpmak onun doğrultusunu değiştirir. Eğer -1 ile çarpılırsa dolayısıyla sadece yönü değişir ama büyüklüğü değişmez.
Skaler çarpma işleminde ne olduğunu görmek için birim vektörlerin birbirlerine dik olmalarından kaynaklı sonucu göz önünde bulundurmak gerekir. Nokta çarpımda gelen ifade kosinüs olduğundan, bu birim vektörlerin kendileriyle çarpımı 1 değerini (çünkü cos(0°)=1\cos(0°)=1), kendileri arasındaki çarpımı ise 0 değerini (çünkü cos(90°)=0\cos(90°)=0) verir.
x^⋅x^=y^⋅y^=z^⋅z^= 1x^⋅y^=x^⋅z^=y^⋅z^=0\Large \hat{\bold{x}}\cdot \hat{\bold{x}} = \hat{\bold{y}}\cdot \hat{\bold{y}} = \hat{\bold{z}}\cdot \hat{\bold{z}} = 1 \newline \hat{\bold{x}}\cdot \hat{\bold{y}} = \hat{\bold{x}}\cdot \hat{\bold{z}} = \hat{\bold{y}}\cdot \hat{\bold{z}} = 0
Dolayısıyla skaler çarpımlarda bileşenlerle ilgili aşağıdaki ifadeye ulaşırız.
A⋅B=(Axx^+Ayy^+Azz^)⋅(Bxx^+Byy^+Bzz^)=(AxBx)+(AyBy)+(AzBz)\large \bold{A} \cdot \bold{B} = (A_x \hat{\bold{x}} + A_y \hat{\bold{y}} + A_z \hat{\bold{z}}) \cdot (B_x \hat{\bold{x}} + B_y \hat{\bold{y}} +B_z \hat{\bold{z}}) \newline =(A_xB_x)+(A_yB_y)+(A_zB_z)
Böylelikle neden iki vektörün skaler çarpımının bir skaleri verdiği daha rahat bir şekilde görülür. Çünkü birim vektörlerin çarpımlarından ya 1 değeri gelerek sadece ilgili katsayı çarpımlarını bırakır ya da 0 gelerek tüm terimi yok eder.
Ayrca herhangi bir A\bold{A} vektörünün, herhangi bir birim vektörle olan skaler çarpımı, A\bold{A}'nın o doğrultudaki bileşenini verir. Bu durumun bir benzerini aşağıdaki eşitlikte görebilirsiniz.
A⋅A=Ax2+Ay2+Az2A=Ax2+Ay2+Az2\Large \bold{A}\cdot \bold{A} = A_x^2+A_y^2+A_z^2 \newline A=\sqrt{A_x^2+A_y^2+A_z^2}
Vektörel çarpımda ise birim vektörlerin çarpımı daha önce bahsettiğimiz sağ el kuralı ile belirlenebilir.
x^×x^=y^×y^=z^×z^=0x^×y^=−y^×x^=z^y^×z^=−z^×y^=x^z^×x^=−x^×z^=y^\Large \hat{\bold{x}}\times \hat{\bold{x}} = \hat{\bold{y}}\times \hat{\bold{y}} = \hat{\bold{z}}\times \hat{\bold{z}} = 0 \newline \hat{\bold{x}}\times \hat{\bold{y}} = -\hat{\bold{y}}\times \hat{\bold{x}}=\hat{\bold{z}} \newline \hat{\bold{y}}\times \hat{\bold{z}} = -\hat{\bold{z}}\times \hat{\bold{y}}=\hat{\bold{x}} \newline \hat{\bold{z}}\times \hat{\bold{x}} = -\hat{\bold{x}}\times \hat{\bold{z}}=\hat{\bold{y}}
Bu nedenle,
A×B=(Axx^+Ayy^+Azz^)×(Bxx^+Byy^+Bzz^)=(AyBz−AzBy)x^+(AzBx−AxBz)y^+(AxBy−AyBx)z^\large \bold{A} \times \bold{B} = (A_x \hat{\bold{x}} + A_y \hat{\bold{y}} + A_z \hat{\bold{z}}) \times (B_x \hat{\bold{x}} + B_y \hat{\bold{y}} +B_z \hat{\bold{z}}) \newline =(A_yB_z-A_zB_y)\hat{\bold{x}} +(A_zB_x-A_xB_z)\hat{\bold{y}}+(A_xB_y-A_yB_x)\hat{\bold{z}}
olacaktır. Bunu ilk bakışta karışık bulabilirsiniz. Fakat aslında bu bir determinant olarak yazılabilir ve böylesi oldukça akılda kalıcıdır.
A×B=∣x^y^z^AxAyAzBxByBz∣\Large \bold{A} \times \bold{B} = \begin{vmatrix}
\hat{\bold{x}} & \hat{\bold{y}} & \hat{\bold{z}} \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{vmatrix}
Üçlü Çarpımlar
Şu zamana kadar gösterdiklerimiz ikili ilişkileri inceliyordu. Fakat elbette olay iki taneyle sınırlı olmak zorunda değil, bunun için üçlü çarpımları da ele almakta fayda var. Bazıları biraz uğraştırıcı olsa da aslında bunları kendiniz de bulabilirsiniz.
A⋅(B×C)=B⋅(C×A) =C⋅(A×B) A⋅(C×B)=B⋅(A×C)=C⋅(B×A)A⋅(B×C)=(A×B)⋅C\Large \bold{A} \cdot (\bold{B}\times \bold{C}) = \bold{B} \cdot (\bold{C}\times \bold{A}) = \bold{C} \cdot (\bold{A}\times \bold{B}) \newline \bold{A} \cdot (\bold{C}\times \bold{B}) = \bold{B} \cdot (\bold{A}\times \bold{C}) = \bold{C} \cdot (\bold{B}\times \bold{A}) \newline \bold{A} \cdot (\bold{B}\times \bold{C}) = (\bold{A} \times \bold{B})\cdot \bold{C}
Buradaki geometrik anlama dikkatinizi çekmek isterim. Bunları sadece tuhaf sembollerle ifade edilen bir matematik olarak görmemeli ve bir fizikçi bakış açısıyla anlamına odaklanmalısınız. Daha önce ∣B×C∣|\bold{B}\times \bold{C}| için taban alanı ifadesini kullanmıştık, bu durumda ∣A⋅(B×C)∣|\bold{A}\cdot (\bold{B}\times \bold{C})| ifadesi A\bold{A}, B\bold{B} ve C\bold{C} tarafından oluşturulan paralel yüzlünün hacmidir. Çünkü ∣Acosθ∣|\bold{A} \cos θ| yüksekliktir.
Son ifadede skaler çarpımla vektörel çarpımın kendi arasında yer değişebildiğine dikkat edin. Bunun manasını artık çıkarabiliyor olmalısınız, eğer neden böyle olduğunu anlayamıyorsanız, önceki paragrafın anlamı üzerinde biraz daha durmalısınız. Ayrıca,
A×(B×C)=B(A⋅C)−C(A⋅B)(A×B)×C=−C×(A×B)=−A(B⋅C)+B(A⋅C)\large \bold{A} \times (\bold{B}\times \bold{C}) = \bold{B}(\bold{A}\cdot \bold{C}) - \bold{C}(\bold{A}\cdot \bold{B}) \newline (\bold{A} \times \bold{B}) \times \bold{C} = - \bold{C} \times (\bold{A} \times \bold{B}) = -\bold{A}(\bold{B}\cdot \bold{C}) + \bold{B}(\bold{A}\cdot \bold{C})
olacaktır. Bu da vektörel çarpımın asosiye olmadığını gösterir. Bunu ispatlamak için keyfi birim vektörler alarak bir karşılaştırma yapabilirsiniz.
Konum, Yer Değiştirme ve Ayrılık Vektörleri
Koordinatları, bir cismin ya da bir olayın nerede gerçekleştiğini ifade etmek için kullandığımızdan bahsetmiştik. Bu noktada yeni bir tanım yaparak, başlangıçtan ilgili noktaya olan bir vektör tanımlayıp buna konum vektörü adını vereceğiz.
r≡xx^+yy^+zz^\Large \bold{r} \equiv x \hat{\bold{x}}+y \hat{\bold{y}}+z \hat{\bold{z}}
Başlangıçtan olan uzaklığı ise,
r=x2+y2+z2\Large r=\sqrt{x^2+y^2+z^2}
olarak ifade edebiliriz. Bu durumda ilgili birim vektör aşağıdaki gibi tanımlanır.
r^=rr=xx^+yy^+zz^x2+y2+z2\Large \hat{\bold{r}}=\frac{\bold{r}}{r} = \frac{x \hat{\bold{x}}+y \hat{\bold{y}}+z \hat{\bold{z}}}{\sqrt{x^2+y^2+z^2}}
Sonsuz küçük yer değiştirme vektörü ise aşağıdaki gibi tanımlanır.
dl=dxx^+dyy^+dzz^\Large d\bold{l}=dx \hat{\bold{x}}+dy \hat{\bold{y}}+dz \hat{\bold{z}}
Genellikle iki nokta arasındaki kıyaslamalarımız söz konusu olduğundan, bu iki cisim veya olay arasındaki ayrıklığı ifade etmek için ayrıklık vektörü tanımlarız.
Υ≡r−r′\Large \bold{\Upsilon}\equiv \bold{r}-\bold{r'}
Büyüklüğü ise aşağıdaki gibi ifade edilir.
Υ=∣r−r′∣\Large \bold{\Upsilon}= |\bold{r}-\bold{r'}|
Birim vektör ise aşağıdaki gibi tanımlanır.
Υ^=ΥΥ=r−r′∣r−r′∣\Large \hat{\bold{\Upsilon}} = \frac{\bold{\Upsilon}}{\Upsilon}=\frac{\bold{r}-\bold{r'}}{|\bold{r}-\bold{r'}|}
Düzeltmeler: Dot producttaki hata düzeltildi.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 8
- 5
- 5
- 5
- 3
- 1
- 1
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 19/04/2024 07:01:37 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12872
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.




