Project Euler 2: Çift Fibonacci Sayıları

- Özgün
Project Euler 2: Fibonacci dizisindeki her yeni terim, önceki iki terimin toplamıdır. 1 ve 2'den başlanarak ilk 10 terim şu şekildedir: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... Dört milyonu aşmayacak şekilde çift Fibonacci terimlerinin toplamı nedir?Project Euler 2 sorusuyla birlikte algoritma sorularının vazgeçilmezi olanFibonacci dizisiyle karşılaşıyoruz. Fibonacci dizilerini elde edebileceğiniz birçok algoritma mevcut, mutlaka bunlara göz atmanızı öneririm. Özellikle özyinelemeli (recursive) fonksiyonlar konusunun vazgeçilmez örneklerindendir. Burada oldukça basit bir metodu kullanacağım. Öncelikle Fibonacci dizisini elde edeceğimiz algoritmayı belirleyelim, ardından 4000000'a kadar olan bu sayılardan hangileri çift onlara bakacağız ve çift olanların toplamının kaç ettiğini bulacağız.
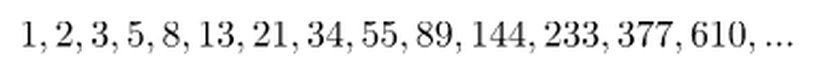
Sıradaki terim f2+f3 olacak. Fakat bunu elimizdeki üç değişkeni kullanarak yapmalıyız, çünkü her seferinde yeni bir değişken tanımlayamayız. Zaten tanımlayabilseydik bile bu çok verimsiz bir yöntem olurdu. Bunun yerine değişkenleri öteleyeceğiz. Yeni sıralamamızdaki ilk terim şu an elimizde olan f2 olacak, dolayısıyla onu f1 yapıyoruz. Şu an elimizde bulunan f3'ü ise f2 yapıyoruz. Böylelikle sayılarımızı birer ötelemiş olduk. Şimdi yapacağımız sıradaki sayıyı belirleme işlemi yine f1+f2 olacak, fakat bu değişkenler önceki değişkenler olduğundan aslında eskiye göre yaptığımız işlem f2+f3 oldu ki biz de tam olarak bunu istiyorduk.
C# Çözümü

Python Çözümü
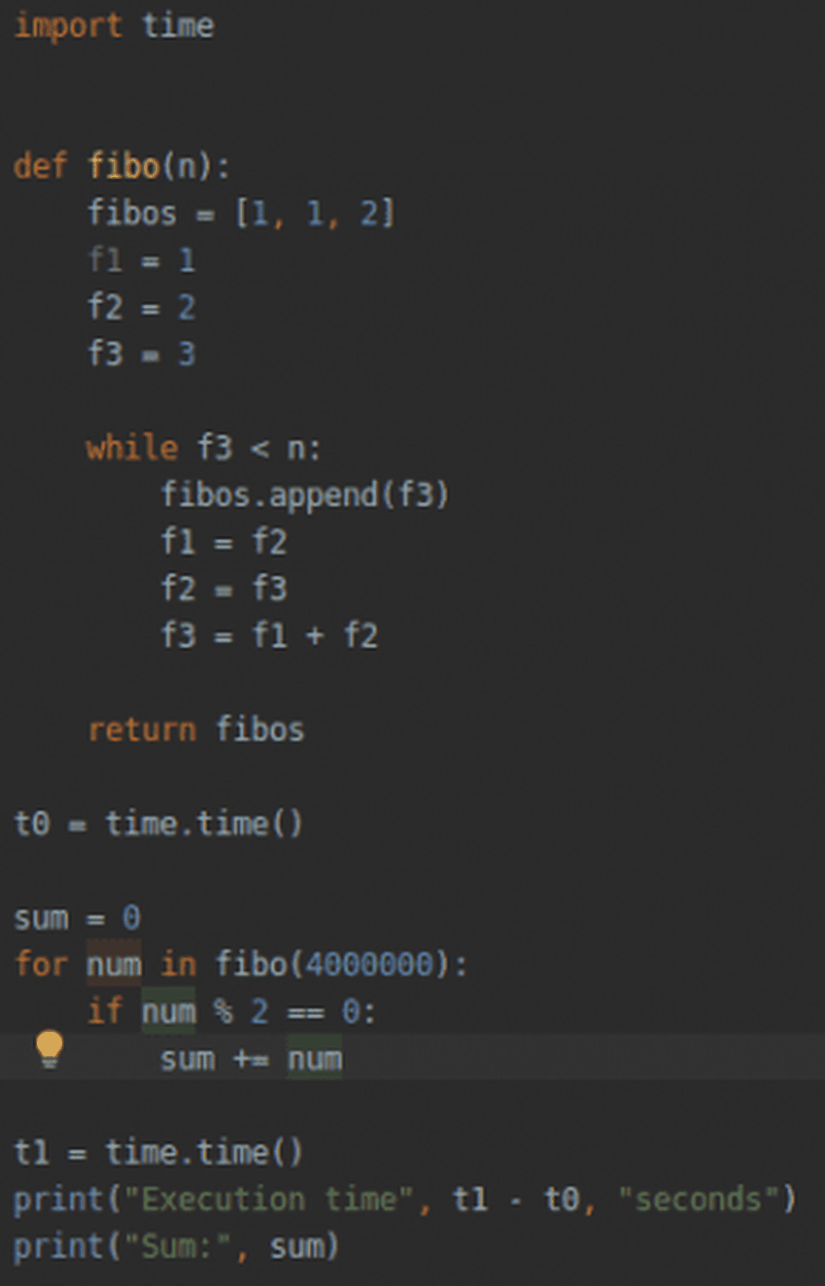
Sum: 4613732
Matematiksel Yaklaşım
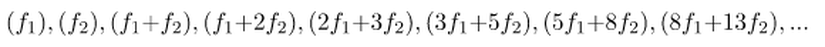
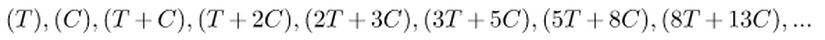
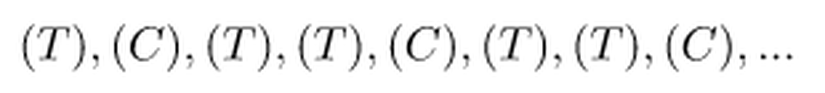
Lakin Fibonacci sayı dizimiz oldukça kısa olduğundan, bu işlemin süre açısından çok da faydalı olmayacağını fakat başka sorularda işimize yarayabilecek bir bakış açısı olduğuna dikkat edelim.
Ögetay Kayalı
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 26/04/2024 02:33:38 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12646
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.


