Pisagor Teoremi Nedir? Pisagor Kimdir?
 Wikimedia Commons
Wikimedia Commons
- Özgün
- Matematik Tarihi
- Bilim Tarihi
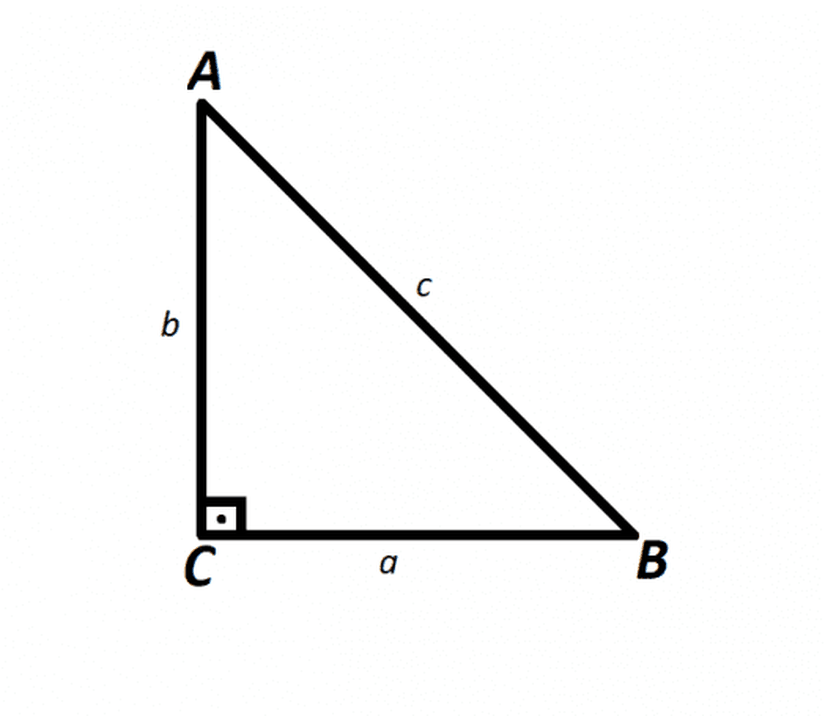
Pisagor teoremine göre bir dik üçgenin iki dik kenarının uzunluklarının kareleri toplamı, "hipotenüs" olarak adlandırılan üçüncü kenarın uzunluğunun karesine eşittir. Bu teorem adını ünlü Yunan düşünür Pisagor'dan alır.
Eğer üçgenin birbirine dik olan iki kenarına aa ve bb, hipotenüse de cc dersek Pisagor teoremini şu şekilde ifade edebiliriz:
a2+b2=c2\Large a^2+b^2=c^2
Bu denklem, aslında Öklidyen geometride geçerlidir. Fakat eğitim hayatlarımızın önemli bir süresi boyunca sadece Öklidyen geometride çalıştığımız için bu durum genellikle göz ardı edilir. Pisagor'dan bu yana Pisagor teoremi üzerinde çalışan matematikçiler, nn pozitif bir doğal sayı olmak üzere aşağıdaki maddelerin sağlandığı genellemesine ulaşmıştır:
a=2n+1\Large a = 2n + 1
b=2n2+2n\Large b = 2n^2 + 2n
c=2n2+2n+1\Large c = 2n^2 + 2n + 1
eşitliklerini sağlayan tüm aa, bb ve cc doğal sayıları, a2+b2=c2a^2+ b^2= c^2 eşitliğini de sağlar.[1]
Bu teoreme göre dik üçgen oluşturabilecek çeşitli tamsayı kümeleri vardır. Örneğin (3,4,5)(3, 4, 5) bunlardan biridir çünkü 32+42=523^2 + 4^2 = 5^2 eder. Bu kombinasyon ve bunun türevleri, Antik Mısır, Çin, Babil ve Hint uygarlıklarında genellikle inşaat işlerinde kullanılmıştır. Ancak şu an kısa bir cümle ile teoremi anlatabiliyorsak bunu Pisagor'a borçlu olduğumuz söylenebilir, çünkü bin küsur yıldır kullanılan yöntemi gözlemleyip formülleştiren kendisi olmuştur.[2], [3]
Efsaneye göre Pisagor, sarayda Samos tiranı Polycrates'i beklerken sıkılır ve yerdeki fayans döşemeyi incelemeye başlar. Buradaki motiften, dik üçgenlerin hipotenüs kenarındaki karelerin alanlarının, diğer iki kenardaki karelerin alanlarına eşit olduğunu fark eder ve sonrasında ünlü Pisagor teoremini geliştirir.[2]
Pisagor Teoreminin Deneyi
Pisagor teoreminin birçok ispatı vardır. Fakat insanlar olarak bazen bazı şeyleri gözle görmek, konuyu çok daha iyi kavramamızı sağlayabiliyor. Bu nedenle Pisagor teoremini, görsel olarak basit bir deneysel doğrulama yaparak, özellikle bu konuyu yeni öğrenen öğrencilere çok daha açıklayıcı bir biçimde anlatabilirsiniz. Aşağıdaki GIF bize bunu harika bir şekilde gösteriyor.
Pisagor Kimdir?
Yerdeki döşemeye bakıp hem kendi adıyla anılacak hem de asırlar boyunca kullanılacak bir teorem geliştirmek Pisagor'un büyük bir şansı gibi görünebilir fakat Pisagor'un şansı, o anda orada bulunması değil, Miletli Thales gibi önemli bir öğretmene sahip olmuş olmasıydı. Thales sayesinde matematik ve astronomiyle tanışmış ve yine onun sayesinde Mısır'a bu alanlarda eğitim görmeye gidebilmişti.
Pisagor'un gördüğü eğitim, matematiğin doğadaki yerini ve önemini kavramasını sağlamıştı. Doğanın ve doğadaki düzenin sayılarla açıklanabileceğine inanıyordu. Bu nedenle tek, çift, üçgensel ve mükemmel sayıların özelliklerini inceledi.
Pisagor ve takipçilerinin tarihte büyük bir yeri var, ancak bunun tek nedeni elbette Pisagor'un dik üçgenlerle ilgili teoremi değil. Bunun yanında geometriye bilimsel bir bakış getirmeleri, bulgularını sistemli kanıtlara dayandırmaları da onların önemini artırdı.[2]
Öklid'in İspatı
Bugün bile neredeyse aynen kullandığımız, Öklid'in Elementler adlı eserinin oluşmasına da Pisagor zemin hazırlamıştır. Elementler'de Öklid, Pisagor bağıntısını aşağıdaki resim üzerinden ispatlar.
 Wikimedia
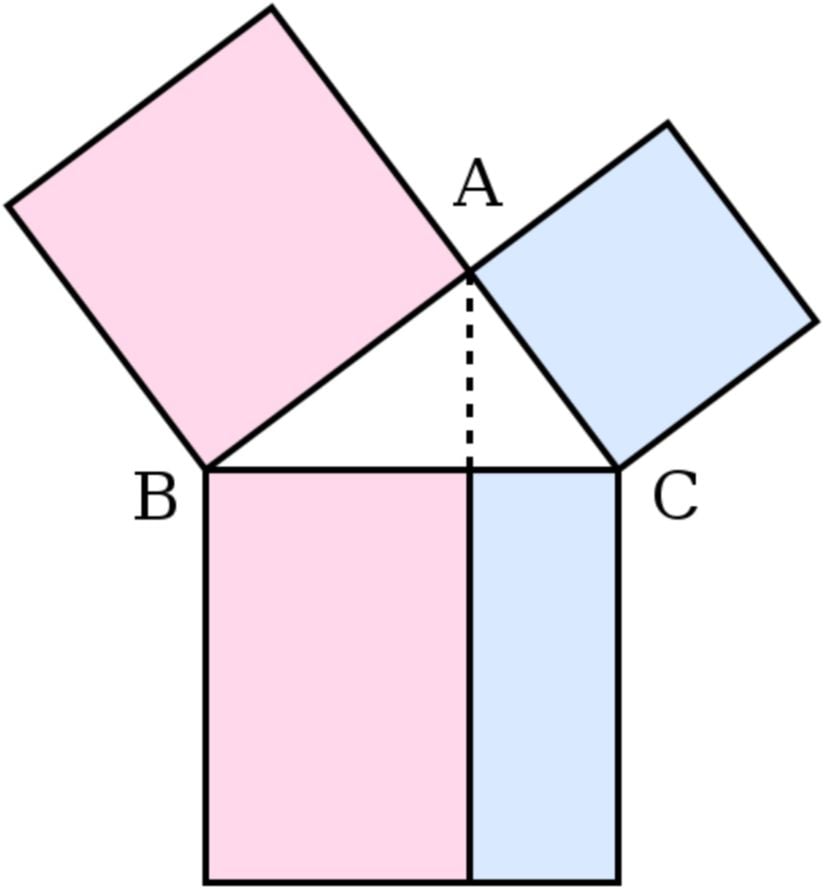
WikimediaÖncelikle AA açısı dik olacak şekilde bir ABCABC üçgeni çizer. Bir kenarı ABCABC üçgenin kenar uzunlukları kadar olan kareleri, bu üçgenin etrafına yerleştirir ve AA köşesinden DEDE kenarına bir dikme indirir. İspatın sonunda pembe alanlar ile mavi alanların birbirine eşit olduğunu ortaya koyar ve bu da iki küçük karenin alanları toplamının hipotenüsteki karenin alanına eşit olduğu anlamına gelir.
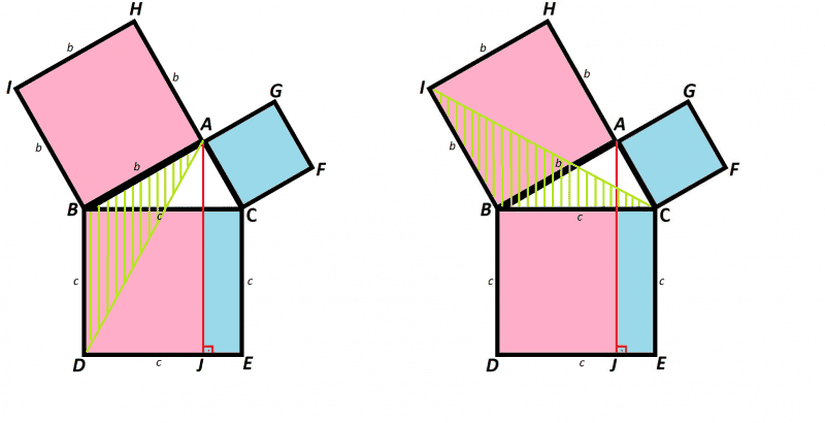
Yukarıda gösterildiği gibi DADA ve ICIC doğru parçalarını çizdiğimizde oluşan içi taralı yeşil üçgenlerin alanları birbirine eşit olur. Çünkü DBADBA ile IBCIBC açıları ve bu açıyı oluşturan kolların uzunlukları (bb ve cc kenarları) birbirine eştir. Kenar-açı-kenar benzerliğinden bu iki üçgenin eş üçgenler olduğunu söyleyebilir ve buradan da alanlarının da eşit olacağı sonucuna varabiliriz.
Aynı iki doğru arasında bulunan ve taban uzunlukları eşit olan bir dikdörtgen ve üçgenden, dikdörtgenin alanı üçgenin alanının iki katı olur. Bu durumda BDJK dikdörtgeninin alanı, BDA üçgenininkinin iki katı (ikisi de BD ve AJ paralel doğruları arasında); BAHI karesinin alanı da IBC üçgenininkinin (her ikisi de IB ve HC paralel doğruları arasında) iki katı olur. Üçgenlerin alanı eşit olduğundan, belirtilen dikdörtgenlerin alanları da eşit olacaktır.
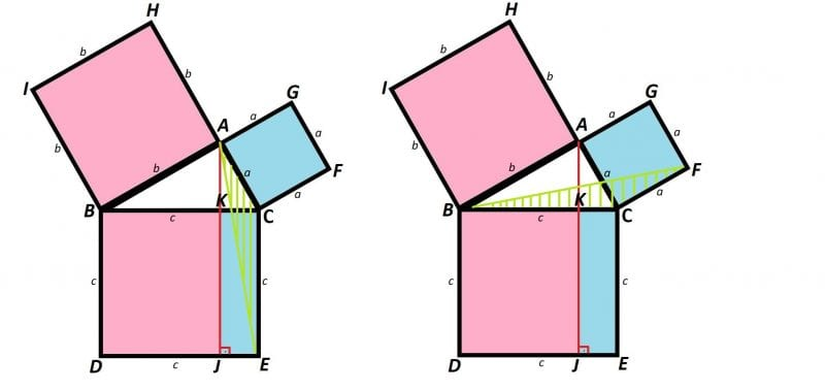
Yukarıda belirtilen işlemlerin aynısını bu kez de AEAE ve AFAF doğru parçalarını çizerek mavi taralı alanlar için yaptığımızda, bunların da birbirine eşit olduğunu görürüz.
Sonuçta mavi alanlar birbirine, pembe alanlar da birbirine eşitse karenin alan formülü gereği a2+b2=c2a^2 + b^2 = c^2 demek mümkündür ve bu da bize Pisagor teoremini verir.[3]
Bhaskara'nın İspatı
Tarih boyunca Pisagor teoremi birçok matematikçinin ilgi odağı olmuş ve 300’den fazla ispatı yapılmıştır.[4] Bhaskara da 12. yüzyılda yaşamış ve bu teoremle ilgilenmiş Hint bir matematikçidir.[5] Bhaskara, ispatına bir dik üçgen ile başlar. Şekildeki bu üçgene ABCABC üçgeni diyelim.
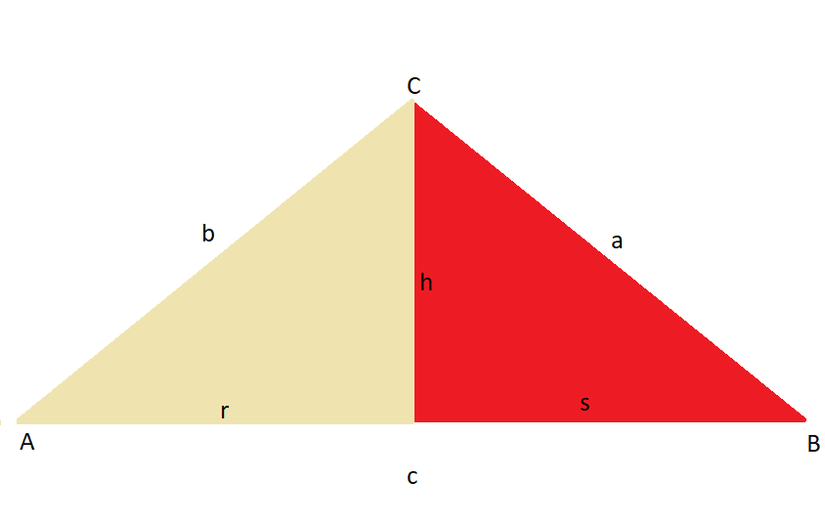
Daha sonra bu üçgenin hipotenüs kenarına bir dikme indirelim (hh ile gösterilen yer). Bu durumda üçgende benzerlik kuralları gereği (açı-açı benzerliği) CBECBE (üçgenin sağ yarısı) veABC ABC (büyük üçgen) üçgenleri benzer olurlar çünkü BB açısı ortaktır ve EE ile CC açıları her iki üçgenin de dik olan açılarıdır. Sonuç olarak bu iki üçgenin tüm iç açıları birbirine eşit olduğundan benzerlerdir diyebiliriz. Benzer olan bu iki üçgen arasında s/a=a/cs/a = a/cbağıntısını yazmak mümkündür. Eşitliğin her iki tarafını da acac ile çarptığımızda da sc=a2sc = a^2 sonucunu elde ederiz.
Bir önceki paragrafta belirtilenle aynı benzerlik kuralları gereği AECAEC üçgeni (üçgenin sol yarısı) ile ACBACB (büyük üçgen) üçgenleri de benzerdir. Bu durumda r/b=b/cr/b = b/c eşitliğini yazabiliriz. Eşitliğin her iki tarafını bcbc ile çarptığımızda ise rc=b2rc = b^2 sonucunu elde ederiz.
Bulduğumuz bu iki sonucu toplarsak sc+rc=a2+b2sc + rc = a^2 + b^2 olur. Eşitliğin sol tarafını cc parantezine aldığımızda şu denklem elde edilir:
- Dış Sitelerde Paylaş
c(s+r)=a2+b2\Large c(s + r) = a^2 + b^2
cc kenarı ise ss ve rr kenarlarının toplamına eşittir, diğer bir deyişle c=s+rc = s + r ise denklem şöyle yazılabilir:
c2=a2+b2c^2 = a^2 + b^2
Bu da Pisagor teoreminin kendisidir.[6]
Pisagor Üçgeni ile Alanlar Arasındaki İlişki
Pisagor teoremi, bir dik üçgenin kenar uzunluklarıyla ilgili bir eşitlik olmasının yanında, bu kenarlara yerleştirilecek düzgün şekillerin alanlarıyla da ilgili bir bağıntı verir. Zaten eğer hatırlayacak olursanız, efsaneye göre de Pisagor bu denkleme fayans döşemelerinin alanlarından yola çıkarak varmıştır.
Şekilde gösterilen dik üçgende bir kenar uzunluğu aa, bb ve cc kenarlarına eşit olacak şekilde, aynı (hepsine üçgen, hepsine beşgen vb.) düzgün geometrik şekiller yerleştirdiğimizde, aa ve bb kenarındaki şekillerin alanları toplamı, cc kenarındakinin alanına eşit olur. Bu şekillere üçgenin her bir kenarını çap kabul eden daireler de dâhildir. Aşağıdaki görselde ne demek istediğimizi daha iyi anlayabilirsiniz.
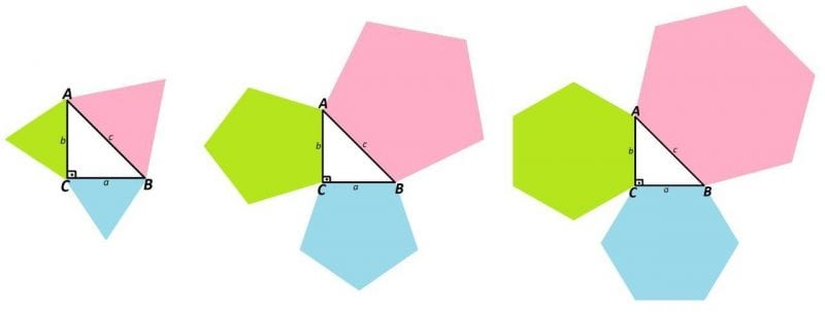
Buradaki her üç şekil için de yeşil ve mavi alanların toplamı, pembe alana eşittir.[1]
Hiperbolik Üçgen ve Pisagor Bağıntısı
Hiperbolik geometri, Öklid'in beş aksiyomundan ilk dördünün geçerliliğini kabul ederken beşincisini etmeyen Öklid dışı bir geometridir.[7] Öklid'in beş aksiyomu şöyle sıralanabilir:
- Düz bir doğru parçası, iki noktanın birleştirilmesiyle ifade edilebilir.
- Herhangi bir düz doğru parçası, düz bir doğru üzerinde sonsuza kadar uzatılabilir.
- Herhangi bir düz doğru parçası için, bu parçası yarıçap olan ve bir noktası merkezi olan bir çember çizilebilir.
- Tüm dik açılar birbirine eştir.
- Herhangi bir doğru parçası ve onun üzerinde yer almayan bir nokta için, yalnızca ve yalnızca bir doğru parçası bu keyfi noktadan geçer ama ne kadar uzatılırsa uzatılsın doğruyu kesmez.[8]
Belirttiğimiz gibi hiperbolik geometri Öklid'in beşinci aksiyomunu kabul etmez ve bir doğruya dışındaki bir noktadan en az iki paralel doğru çizilebileceğini söyler.[7] Hiperbolik geometri burada açıklayamayacağımız kadar geniş bir konudur. Fakat hiperbolik üçgen ile Pisagor bağıntısı arasındaki ilişkiyi daha kolay anlatabilmek adına hiperbolik geometrinin ne olduğuna kısaca değindikten sonra konumuza geri döneceğiz.
Pringles'ların yüzeyi hiperbolik yüzeylere güzel bir örnektir. Elinize üçgen oluşturacak şekilde üç parça ip alıp bunları Pringles'ın üzerinde üçgen haline getirdiğinizi hayal edin. Oluşan üçgen alışık olduğumuz gibi dümdüz kenarlara sahip olmayacaktır. İşte bu üçgene hiperbolik üçgen denir ve iç açılarının toplamı 180°’den küçük olur.[9] Elinizdeki iplerle bir dik üçgen yapıp bunu Pringles'ın üzerine yerleştirdiğinizde ise bir hiperbolik dik üçgen elde etmiş olursunuz.
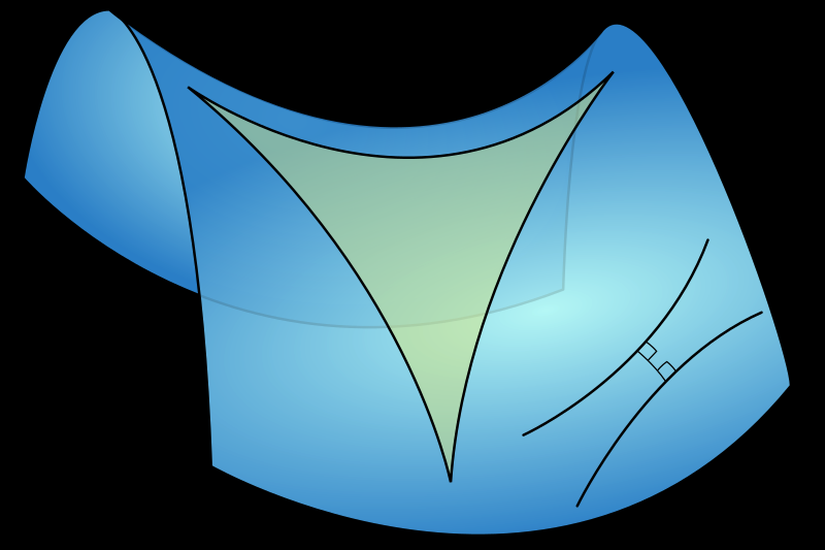
Matematikçiler, Pisagor teoreminin hiperbolik dik üçgenler için de geçerli olup olmayacağını merak etmiş ve bunları incelemişlerdir. Ancak ne yazık ki Pisagor teoremi yalnızca Öklidyen bir geometride geçerlidir. Ancak hiperbolik geometride Pisagor teoremine benzeyen başka bir eşitlik bulunur:[10]
cosh(a).cosh(b)=cosh(c)\Large cosh(a).cosh(b) = cosh(c)
Burada coshcosh, hiperbolik kosinüs fonksiyonudur.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 8
- 6
- 5
- 3
- 1
- 1
- 1
- 0
- 0
- 0
- 0
- 0
- ^ a b R. Aslaner, et al. Kare İçin İfade Edilen Pisagor Bağıntısının Diğer Düzgün Çokgenlere Ve Daireye Uygulanması. (27 Mart 2018). Alındığı Tarih: 10 Ocak 2024. Alındığı Yer: Buca Eğitim Fakültesi Dergisi | Arşiv Bağlantısı
- ^ a b c D. Veljan. (2018). The 2500-Year-Old Pythagorean Theorem. Informa UK Limited, sf: 259-272. doi: 10.1080/0025570X.2000.11996853. | Arşiv Bağlantısı
- ^ a b A. Bogomolny. Euclid's Proof Of Pythagoras' Theorem (I.47). Alındığı Tarih: 10 Ocak 2024. Alındığı Yer: Cut The Knot | Arşiv Bağlantısı
- ^ UMB Faculty. Pythagorean Theorem. Alındığı Tarih: 10 Ocak 2024. Alındığı Yer: UMB Faculty | Arşiv Bağlantısı
- ^ T. E. O. E. Britannica. Bhāskara Ii | 12Th Century Indian Mathematician & Astronomer. (1 Ocak 2024). Alındığı Tarih: 10 Ocak 2024. Alındığı Yer: Encyclopedia Britannica | Arşiv Bağlantısı
- ^ A. Head. Proofs Of The Pythagorean Theorem. Alındığı Tarih: 10 Ocak 2024. Alındığı Yer: Jim Wilson | Arşiv Bağlantısı
- ^ a b T. E. O. E. Britannica. Hyperbolic Geometry | Non-Euclidean, Lobachevsky, Bolyai. Alındığı Tarih: 10 Ocak 2024. Alındığı Yer: Encyclopedia Britannica | Arşiv Bağlantısı
- ^ E. W. Weisstein. Euclid's Postulates. Alındığı Tarih: 10 Ocak 2024. Alındığı Yer: Wolfram Mathworld | Arşiv Bağlantısı
- ^ Uncommon Nonsense. Hyperbolic Geometry: An Introduction. Alındığı Tarih: 10 Ocak 2024. Alındığı Yer: YouTube | Arşiv Bağlantısı
- ^ S. Taylor. Pythagoras In The Hyperbolic Plane. Alındığı Tarih: 10 Ocak 2024. Alındığı Yer: The Geometric Viewpoint | Arşiv Bağlantısı
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 26/04/2024 04:33:08 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12873
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.





