Paralelkenar Nedir? Paralelkenar ile İlgili Formüller ve Özellikler Nelerdir?
 Exemplore
Exemplore
- Özgün
- Geometri
Paralelkenar, karşılıklı kenarları birbirine paralel ve karşılıklı iç açıları birbirine eşit olan dörtgendir. Bu tanımdan yola çıkarak tüm dikdörtgenlerin ve eşkenar dörtgenlerin özel birer paralelkenar olduğu sonucuna varabiliriz. Örneğin:
- Dikdörtgen, dik açılı bir paralelkenardır.
- Kare, dik açılı ve eşit kenarlı bir paralelkenardır.
- Kapakta paylaştığımız oyun kartlarındaki karo şeklini veren eşkenar dörtgen, eşit kenarlı bir paralelkenardır.
Paralelkenarların Özellikleri Nelerdir?
Bir geometrik cismin "paralelkenar" olabilmesi için, aşağıdaki kurallardan biri doğru olmalıdır:
- İki çift karşıt kenar paralel olmalıdır.
- İki çift karşıt kenar eşit uzunlukta olmalıdır.
- İki zıt açı çifti eşit büyüklükte olmalıdır.
- Köşegenler birbirini ortalamalıdır.
- Zıt kenarlardan bir çifti paralel ve eşit uzunlukta olmalıdır.
- Komşu açılar bütünler açı olmalıdır.
- Her bir köşegen, dörgeni iki eş üçgene bölmelidir.
- Paralelkenar Yasası: Kenar uzunluklarının karelerinin toplamı, köşegenlerin uzunluklarının karelerinin toplamına eşit olmalıdır.
- Rotasyonel simetrisi 2 olmalıdır.
- Viviani Teoremi: İç noktalarından herhangi birinin kenarlara uzaklığının karelerinin toplamı, nokta tercihinden bağımsız olmalıdır.
- Paralelkenar düzlemi içinde öyle bir X\text{X} noktası varıdr ki, X\text{X}'ten geçen bütün düz çizgiler paralelkenarı eşit alana sahip iki bölgeye ayırır.
- Paralelkenarların zıt kenarları tanım gereği paraleldir ve dolayısıyla asla kesişemezler.
- Bir paralelkenarın alanı, köşegenlerinden biri ile üretilen üçgenlerden herhangi birinin alanının 2 katıdır.
- Bir paralelkenarın alanı, iki komşu kenarın vektör çarpımlarının büyüklüğüne eşittir.
- Paralelkenarın ortasından geçen bütün doğrular, paralelkenarı iki eşit alana böler.
- İçten veya dıştan olması fark etmeksizin, bir paralelkenarın her bir kenarına çizilen karelerin merkezleri de bir kare oluşturur (aşağıda gösterilmiştir).
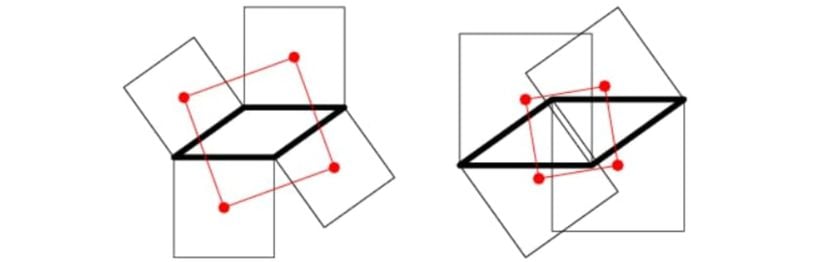
Paralelkenar ile İlgili Formüller Nelerdir?
Paralelkenarda karşılıklı iç açıların birbirine eşit ve karşılıklı kenarların da birbirine paralel olduğunu söyledik. Bu durumun doğal bir sonucu olarak karşılıklı kenar uzunlukları da birbirine eşit olur ve iki komşu iç açı da birbirinin bütünleri olur. Yani iki komşu iç açının toplamı 180° yapar.
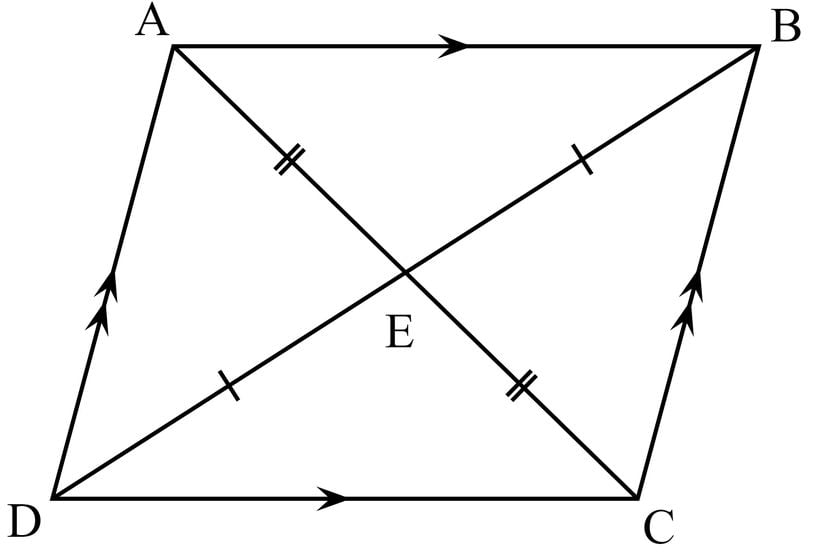
Paralelkenarda Köşegenlerin Özellikleri
Paralelkenarın köşegenleri birbirini ortalar.
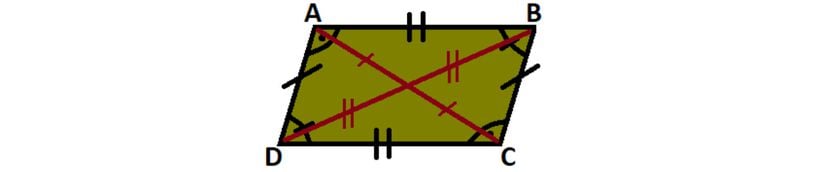
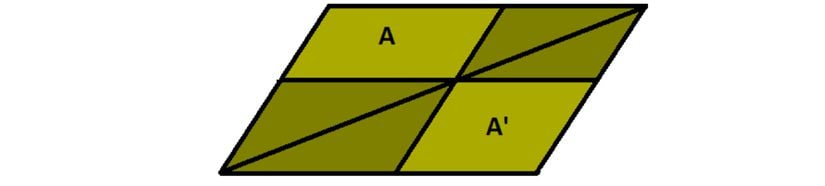
Her bir köşegen, paralelkenarı iki eş parçaya böler. Ancak burada dikkat edilmesi gerekir ki iki köşegen çizildiğinde şeklin alanı dört eş parçaya bölünmüş olmaz. Aşağıdaki şekilde gösterildiği gibi karşılıklı alanlar birbirine eşit olur.
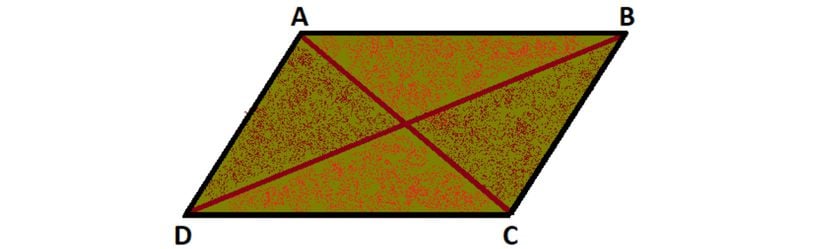
Paralelkenarın bir köşegeni üzerinde kesişecek biçimde, kenarlarına paralel iki doğru parçası çizersek birbiriyle aynı büyüklükte iki alan elde etmiş oluruz. Bu alanların neresi olduğu aşağıdaki şekilde A ve A’ şeklinde gösterilmiştir.
Paralelkenarın Köşegen Uzunluğu Nasıl Hesaplanır?
Aşağıdaki gibi bir paralelkenarımız olsun:
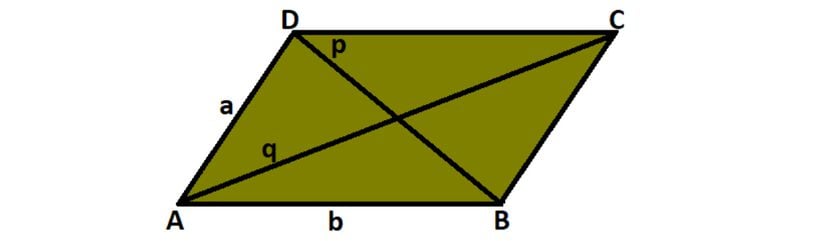
Bir köşegenin uzunluğu, aşağıda belirtilen formüller yardımıyla bulunabilir:
p=q=a2+b2−2abcosA^p=q=\sqrt{a^2+b^2-2ab\cos{\hat{A}}}
veya:
p=q=a2+b2+2abcosB^p=q=\sqrt{a^2+b^2+2ab\cos{\hat{B}}}
Ayrıca paralelkenarın kenarları ve köşegenleri aşağıdaki eşitliği de sağlar:
p2+q2=2(a2+b2)p^2 + q^2 = 2(a^2 + b^2)
Paralelkenarın Çevresi Nasıl Hesaplanır?
Yukarıdaki paralelkenar üzerinden gidecek olursak, paralelkenarın çevresini basitçe şu formülle hesaplayabilirsiniz:
Ç=2(a+b)Ç=2(a+b)
Paralelkenarın Alanı Nasıl Hesaplanır?
Yükseklik Yöntemi
Elimizde şu özelliklere sahip bir paralelkenar olsun:
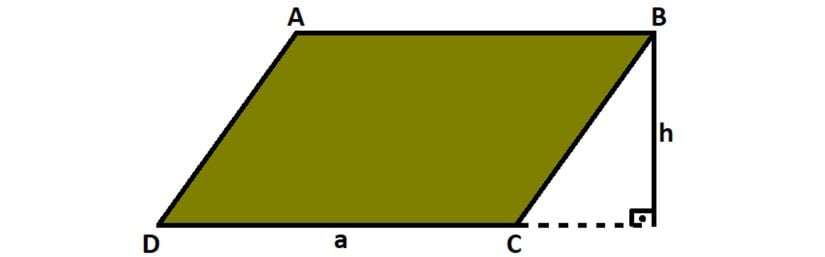
Paralelkenarda alan, yükseklik ile yüksekliğin indiği taban uzunluğunun çarpılmasıyla bulunur. Bunu formüle çevirecek olursak:
A=h×aA = h \times a
Sinüslü Alan Formülü
Tabii paralelkenarda alan bulmanın tek yolu bu değildir. Diğer bir yol ise sinüslü alan formülünü kullanmaktır. Bu formül, esasen bir üçgenin alanını bulmada kullanılır. Üçgenin iki kenar uzunluğu ile bu iki kenarı birleştiren köşenin açısının sinüsü çarpılıp sonuç ikiye bölündüğünde üçgenin alanını elde etmiş oluruz. Daha önce belirttiğimiz üzere paralelkenardaki bir köşegen, paralelkenarı iki eş parçaya, daha doğrusu iki eş üçgene böler. Bu durumda sinüslü alan formülünü kullanır ve ikiyle çarparsak alanı bulmuş oluruz.
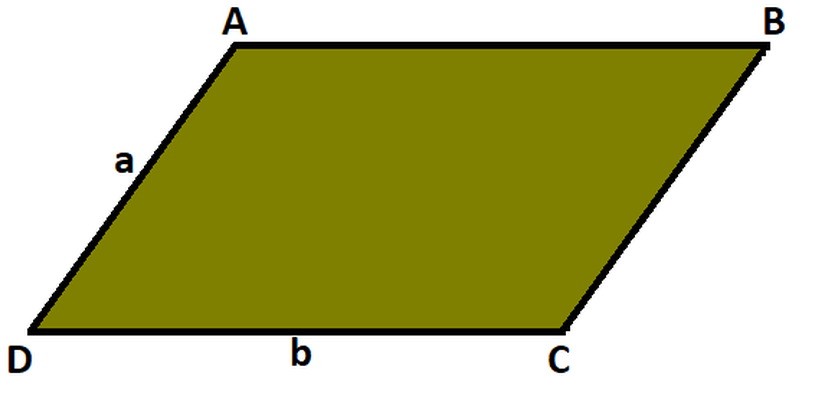
Yukarıdaki görselde alan:
A=a×b×sin(D^)A = a \times b \times \sin(\hat{D})
Şeklinde bulunur. İki bütünler açının sinüs değeri birbirine eşit olacağından D açısı yerine herhangi başka bir açı da kullanılabilir.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 11
- 4
- 3
- 3
- 2
- 2
- 1
- 1
- 1
- 1
- 1
- 1
- E. W. Weisstein. Parallelogram. Alındığı Tarih: 11 Ekim 2022. Alındığı Yer: Wolfram Alpha | Arşiv Bağlantısı
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 20/04/2024 06:58:27 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/13012
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.




