Nükleer Fizik: Alfa Bozunumu

- Özgün
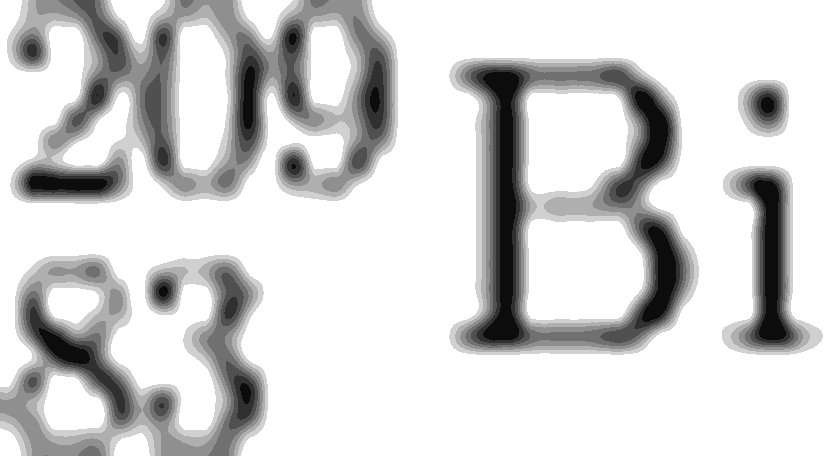
Bu olay gerçekleşirken atom, iki proton ve iki nötrondan oluşan bir parçacık fırlatır. Bu parçacık, basitçe He elementinin çekirdeğidir.
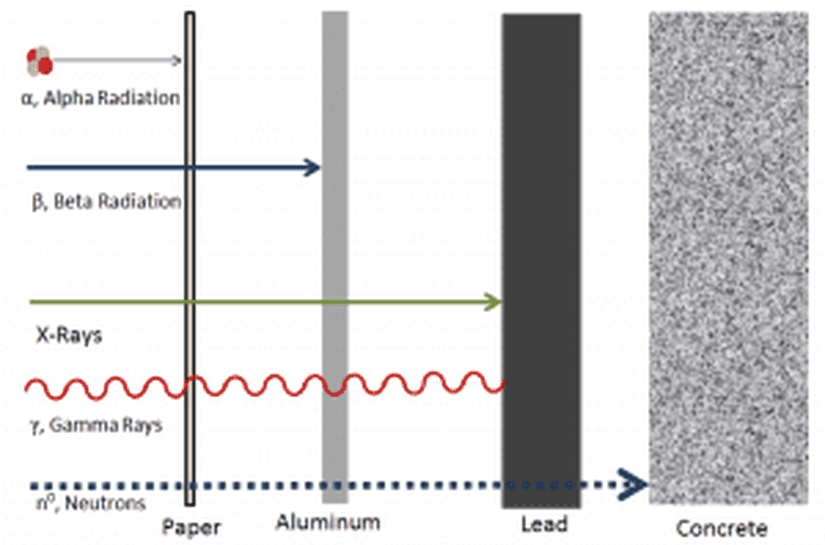
Bu bozunum sonucu ortaya çıkan parçacık, kısmen daha ağırdır. Ancak bu, demek değildir ki, herhangi bir maddenin derinlerine işleyebilir. Aksine, alfa parçacıkları, cisimlerin yüzeyi tarafından kolaylıkla durdurulabilir (Aşağıdaki görseli inceleyiniz). Bu sebepledir ki, tıbbi işlemlerde pek sık kullanılmazlar.
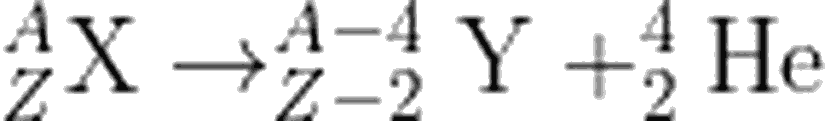
Alfa Parçacığının Kinetik Enerjisi
Enerji ve momentumun korunumu ilkelerini kullanarak bu soruya cevap vermeye çalışalım. Biliyoruz ki, enerji korunumuna göre,
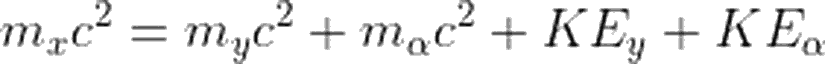
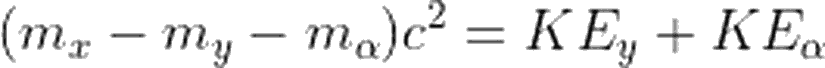
Eğer ki Q sıfırdan büyükse, bozunum kendiliğinden gerçekleşir. Ya da farklı bir deyişle, Eğer alfa bozunumu gerçekleşiyorsa, eşitliğin sol tarafı pozitif olmalıdır.
Şimdi bir de momentumun korunumu için eşitliğimizi yazalım. Atomun ilk durumdaki momentumunu 0 olarak düşünürsek,
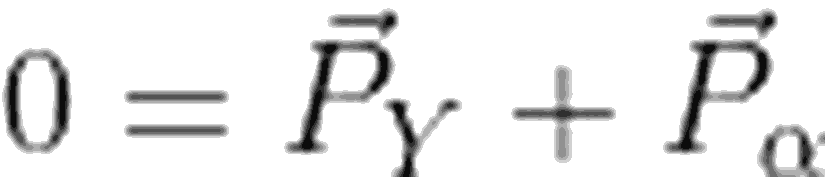
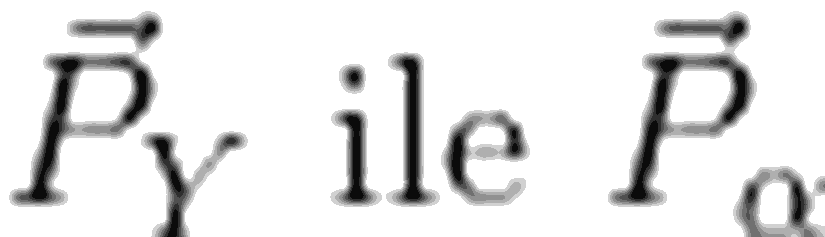
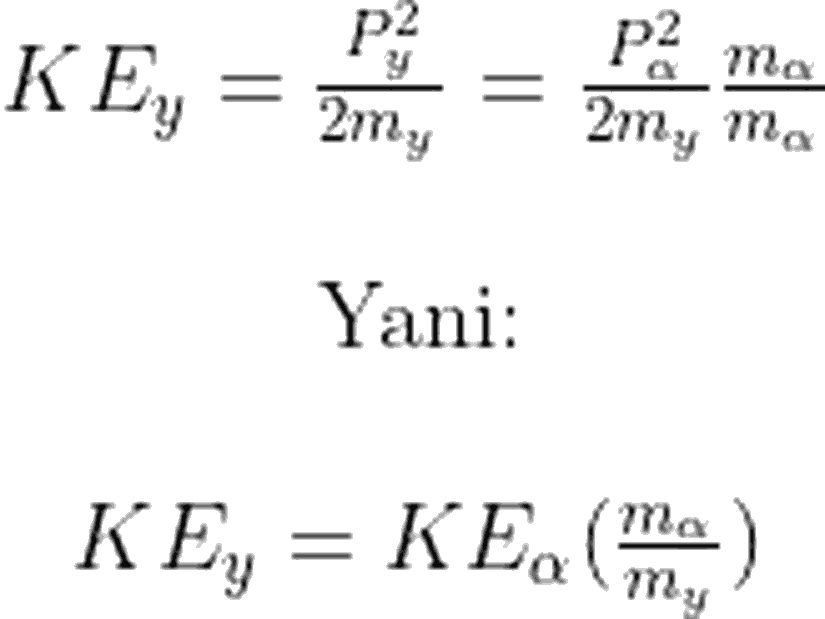
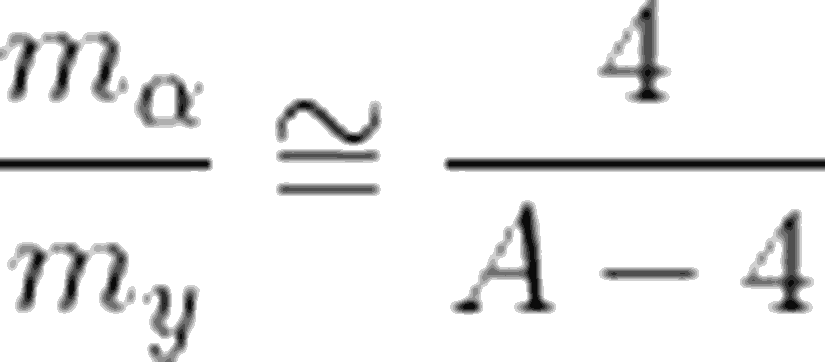
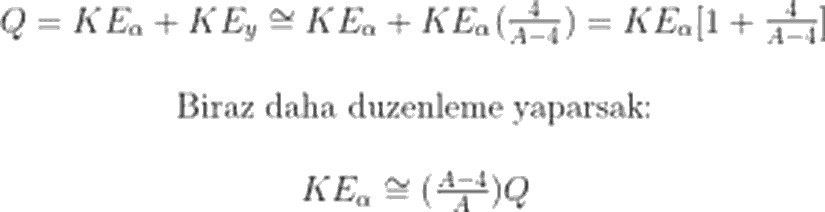
Bu da demektir ki, parçalanma enerjisinin büyük çoğunluğu, alfa parçacığının kinetik enerjisine gider. Geri kalan kısım da, yeni oluşan Y atomunun kinetik enerjisi olur.
Alfa Bozunumuna Bir Örnek
Bir örnek ile bu konsepti pekiştirmek faydalı olacaktır. Örneğin, alfa bozunumuna uğrayan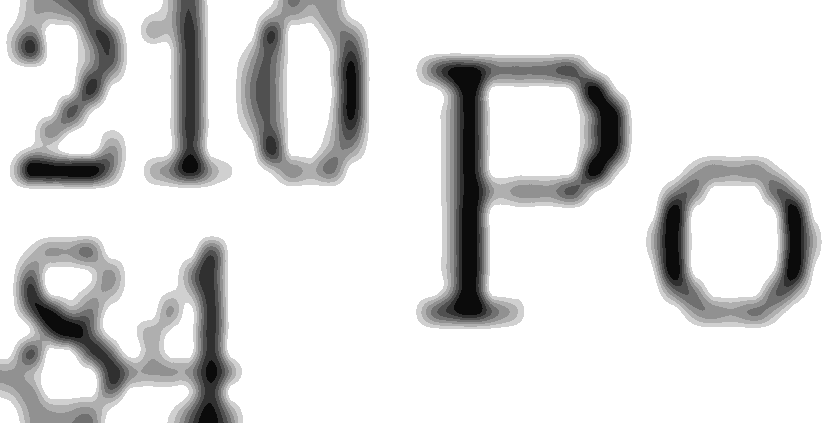
Öncelikle, ilk denklemi denklemi
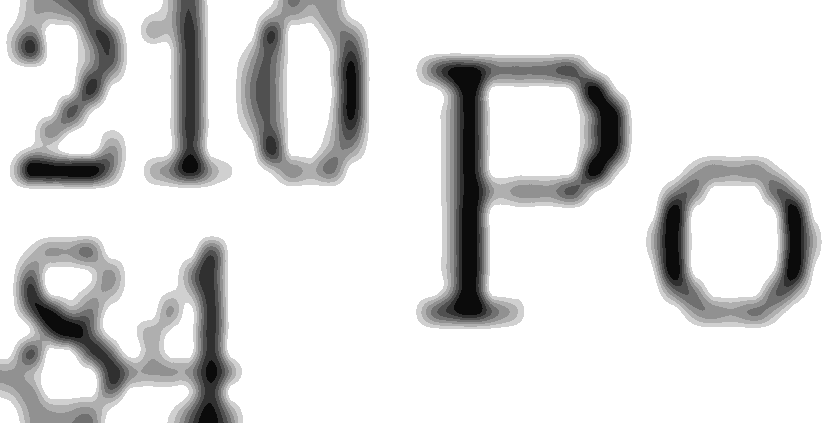
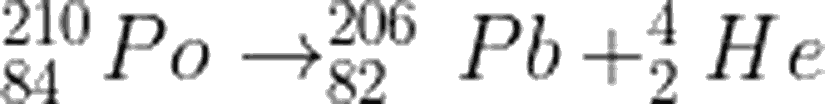
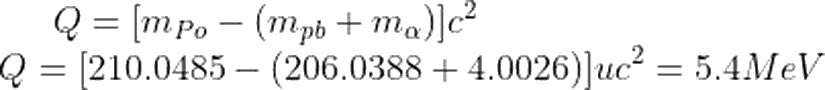
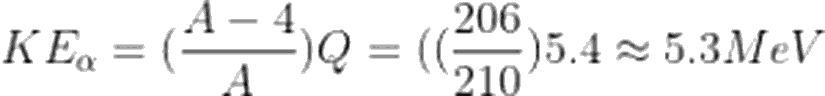
Bu yazımızda, alfa bozunumunu ve bu bozunum sonucu oluşan alfa parçacığının özelliklerini inceledik. İlerleyen yazılarımızda, diğer bozunum türlerini ve bu türlerin etrafımızdaki materyallerle etkileşimlerini inceleyeceğiz.
Ege Can KARANFİL
Referanslar
- Prof. Dr. Selahattin Özdemir, Health Physics ders notları
- Energy Education, "Alpha Decay"
<https://energyeducation.ca/encyclopedia/Alpha_decay>
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 25/04/2024 17:31:20 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12627
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.



