Merkezcil İvme Nedir? Düzgün Dairesel Hareket Formülleri Nelerdir?

- Özgün
- Fizik
Bu yazı dizimizde şu ana dek hep doğrusal bir hareketten konuştuk. Lakin hareket daima doğrusal olmak zorunda değildir, hatta çoğu durumda değildir. Bunun en basit örneği merkezcil ivme tarafından sağlanan düzgün dairesel harekettir. Hiç kuşkusuz bir cisim bir nokta etrafında dairesel bir hareket yapabilir. Bu nokta etrafında sabit bir süratle (dikkat edin hız demiyoruz) yapılan dairesel harekete, düzgün dairesel hareket denir.
Düzgün dairesel hareket sırasında sürat sabittir, hız sabit değildir.
Eğer hatırlayacak olursanız sürat ve hız arasındaki farktan bahsetmiştik. Sürat, hızın skaler karşılığıydı. Dairesel bir hareket sırasında, aşağıdaki animasyonda olduğu gibi sürat her ne kadar sabit kalsa da hız değişir. Çünkü hareket vektörünün yönü dairesel bir hareketi sağlayabilmek adına değişmektedir.
Yönün değişiyor olması, her ne kadar onun büyüklüğü olan sürat değişmese de, bir vektör olduğundan dolayı hızın değişeceği anlamına gelir . Eğer bu kavramlar kafanızı karıştırıyorsa skaler ve vektörel konusuna dönüp bir göz atmanızı muhakkak tavsiye ediyoruz.
Düzgün Dairesel Hareket
Eğer bir cisim dairesel bir hareket yapıyorsa ivmeye sahiptir, çünkü az önce de bahsettiğimiz gibi hızı zamanla değişmektedir ve ivme de hız zamanla değiştiğinde ortaya çıkar. Bir başka deyişle hızın zamanla değişimi sıfır olmadığına göre, bir ivmesi vardır. Dolayısıyla bir cismin dairesel bir hareketi sürdürebilmesi için sürekli olarak merkezcil ivme adını verdiğimiz bir ivme tarafından sağlanan kuvvetle tutulması gerekir. Aksi takdirde cisim doğrusal olan hareketine sabit hızla devam edecektir. Bir başka deyişle eğer hız değişiyorsa, onu değiştiren bir şeyler olmalıdır.
Hız vektörü yola teğettir (tanjant vektörü de deriz). Bu nedenle hız vektörü dairenin yarıçapına daima dik olur. İvme vektörünün yola dik olması gerektiğini sezgilerimiz bize söyler. Bunu şu noktada göstermek aslında oldukça kolaydır.
Merkezcil İvme Formülü ve Yönü
Merkezcil ivme formülünü elde etmek için öncelikle deneyimizi kurmamız gerekir. Farz edelim ki bir cisim dairesel bir hareket yapıyor olsun ve bu hareket sırasında sürati değişmesin (hızının büyüklüğü sabit kalsın). Fakat hız vektörünün yönü biraz değişecektir. Başlangıç noktasını A\text{A}, bitiş noktasını B\text{B} olarak tanımlayalım. O halde ilk hız viv_i, son hız ise vsv_s olsun. Buna karşılık gelen zamanlar da sırasıyla tit_i ve tst_s olsun. Bu durumda şeklimiz şuna benzer:
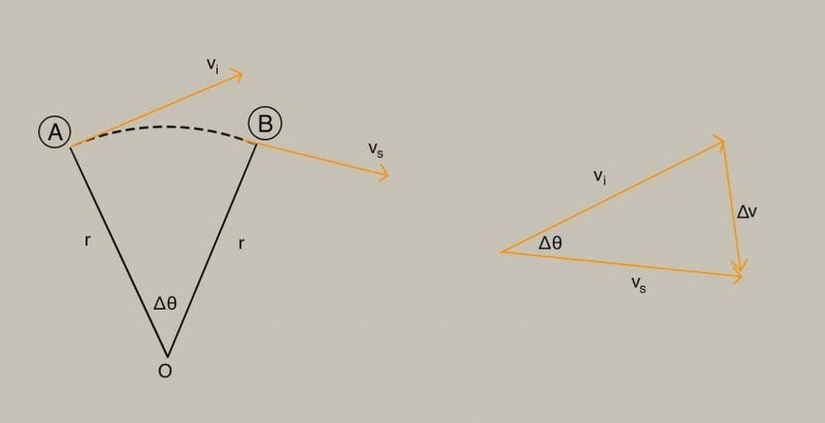
Parçacığın ivmesini hesaplamak oldukça kolaydır. Ortalama ivme ifadesinden faydalanırız.
a=vs−vits−ti=ΔvΔt\Large \bold{a}=\frac{\bold{v_s}-\bold{v_i}}{t_s-t_i}=\frac{\Delta \bold{v}}{\Delta t}
Burada kalın harflerle yazılan a\bold{a} (ivme) ve v\bold{v} (hız) ifadesinin vektör olduğuna dikkat edin. Üzerine vektör işareti koymaktansa kolaylık olması açısından kalın karakterle gösteririz. Dolayısıyla bu ifade bize vsv_s ve viv_i ifadelerinin vektörel olarak birbirlerinden çıkarılıp bir skalere bölüneceğini söyler. Sağdaki şekilden de görüleceği üzere Δv=vs−viΔv=v_s-v_i'dir. Dolayısıyla vektör toplamı olarak yazacak olursak vi+Δv=vsv_i+Δv=v_s olur.
Sağdaki üçgen ile soldaki üçgen benzer olduklarına göre, bunlar arasında bir bağıntı kurabiliriz.
Δvv=Δrr\Large \frac{\Delta v}{v}=\frac{\Delta r}{r}
Bu durumda ΔvΔv için ifadeyi bir önceki ivme ifadesinde yerine yazacak olursak,
a=vΔrrΔt\Large a=\frac{v\Delta r}{r\Delta t}
olarak yazılır. Şimdi düşünmemiz gereken şey limit kavramıdır. Şekildeki A\text{A} ve B\text{B} noktaları arasındaki mesafeler eğer birbirlerine çok yakın olurlarsa ΔtΔt sıfıra yaklaşır, dolayısıyla Δr/ΔtΔr/Δt oranı da vv süratine yaklaşır. Bu durumda Δt→0Δt \rightarrow 0 limitini göz önüne alırsak,
ar=v2r\Large a_r=\frac{v^2}{r}
olduğunu bulmuş oluruz. Bu ifade düzgün dairesel hareket yapan bir cisim için merkezcil ivme formülüdür. Burada görsele geri dönüp odaklanmanız gerekmektedir. Eğer A\text{A} ve B\text{B} birbirine çok yakın olurlarsa, ΔvΔv vektörünün yönünün nereye baktığını anlamaya çalışın. Bu hiç kuşkusuz ivmemizin doğrultusudur ve merkeze doğrudur.
Böylelikle düzgün dairesel hareket yapan bir cisimde, merkezcil ivme için gerekli ifadeyi bulduk ve bunun yönünün merkez doğrultusunda olduğunu da göstermiş olduk.
Sonuçlar ve Yorum
Sadece merkezcil ivme formülüne odaklanıp bitirmeden önce, bunların ne anlama geldiğini düşünmenizi de istiyorum. Algılarınıza kulak vermeniz ve fiziği içselleştirmeniz gereken nokta burasıdır. Her ne kadar denklemi türetirken bunlardan faydalanmış olsak da, sonucumuzdan çıkarım yapmak elzemdir.
Düzgün dairesel hareket yapan bir cismimiz olduğunu varsayarak hareket ettik. Konumu daire etrafında değişse bile süratinin değişmeyeceğini kabul ettik. Lakin hız vektörünün yönü değiştiği için ivmesi olması gerektiğini biliyorduk. Bu nedenle hedefimiz, hızdaki değişimi veren ifadeyi bulmaktı ve bunu yaptık. İlgili geometriyi kurduktan sonra, denklemleri yerine koyduğumuzda, merkezcil ivme formülünü ve onun merkez doğrultusunda olduğunu bulmuş olduk.
Denklemin bize söylediği hız arttıkça merkezcil ivmenin çok daha fazla artacağıdır. Bunun yanında yarıçap küçüldükçe, yani hareket doğrusallıktan ne kadar çok sapmışsa, merkezcil ivmenin de o kadar fazla olacağıdır. Çünkü rr (yarıçap) ile ters orantılıdır.
Merkezcil ivme sıklıkla merkezkaç ile karıştırılır, bu noktada merkezcil ivmeden bahsettiğimizin bir kez daha altını çizmemiz gerek.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 15
- 9
- 4
- 4
- 3
- 1
- 1
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 25/04/2024 07:39:12 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12794
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.




