Lineer cebir (ya da doğrusal cebir), herhangi bir vektör uzayın içindeki lineer denklem ve lineer dönüşümlerin matrisler vasıtasıyla gösteren matematiğin bir dalıdır. Örnek olarak, Newton’un ikinci hareket yasası (F = ma) için net kuvvet vektörünü (Fx, Fy, Fz) olarak ivme vektörünü ise (ax, ay, az) olarak alalım. Ardından yasayı her bir bileşene uygularsak aşağıdaki lineer denklemlere ulaşabiliriz.
Fx = max + 0ay + 0az
Fy = 0ax + may + 0az
Fz = 0ax + 0ay + maz
Bu lineer dönüşüm ise aşağıdaki matris ile gösterilebilir.
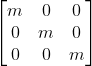
Lineer Cebirde Cisim Nedir?
Matematikte reel sayılar veya karmaşık sayılar kümesini, bu kümeye F diyelim, cisim olarak adlandırabilmemiz için aşağıdaki tüm aksiyomları sağlaması gerekir.
- F’nin elemanı olan tüm x ve y değerleri için, x + y = y + x doğru olmalıdır. Farklı bir deyişle, toplama işleminin değişme özelliği uygulanabilir olmalıdır.
- F’nin elemanı olan tüm x, y ve z değerleri için, x + (y + z) = (x + y) + z doğru olmalıdır. Farklı bir deyişle, toplama işleminin birleşme özelliği uygulanabilir olmalıdır.
- F’nin elemanı olan tüm x değerleri için, x + 0 = x değerini veren “0” F kümesininin elemanı olmalıdır. Farklı bir deyişle, toplama işleminin etkisiz elemanı F’de bulunmalıdır. Ayrıca değişme özelliğinden dolayı, sağ ve sol etkisiz elemanları aynı olacaktır.
- F’nin elemanı olan tüm x değerleri için, x + (-x) = 0 değerini veren “-x” F kümesinin elemanı olmalıdır. Farklı bir deyişle, her F elemanının toplama işlemine göre tersi yine F kümesinin içinde bulunmalıdır. Ayrıca yine değişme özelliğinden dolayı herhangi bir x için sağ ve sol ters elemanları aynı olacaktır.
- F’nin elemanı olan tüm x ve y değerleri için, xy = yx doğru olmalıdır. Yani, çarpma işleminin değişme özelliği uygulanabilir olmalıdır.
- F’nin elemanı olan tüm x, y ve z değerleri için, x(yz) = (xy)z doğru olmalıdır. Yani, çarpma işleminin birleşme özelliği uygulanabilir olmalıdır.
- F’nin elemanı olan tüm x değerleri için, x1 = x değerini veren “1” F kümesininin elemanı olmalıdır. Farklı bir deyişle, çarpma işleminin etkisiz elemanı F’de bulunmalıdır. Ayrıca değişme özelliğinden dolayı, sağ ve sol etkisiz elemanları aynı olacaktır.
- F’nin elemanı olan ve 0’a eşit olmayan x değerleri için, xx-1 = 1 değerini veren “x-1” F kümesinin elemanı olmalıdır. Farklı bir deyişle, her F elemanının çarpma işlemine göre tersi yine F kümesinin içinde bulunmalıdır. Ayrıca yine değişme özelliğinden dolayı herhangi bir x için sağ ve sol ters elemanları aynı olacaktır.
- F’in elemanı olan tüm x, y ve z değerleri için, x(y + z) = xy + xz doğru olmalıdır. Yani, çarpmanın toplama işlemi üzerine dağılma özelliği bütün F elemanları için sağlanabilmelidir.
Bu aksiyomlardan ilk dört aksiyom bize (F, +)’nın ve sonraki dört aksiyom ise (F, .)’nın abelyen grup olduğunu göstermekle beraber eğer setimizde “0 = 1” durumu varsa F’nin tek elemanı vardır o da sıfırdır.
Vektör Uzayı Nedir?
Herhangi bir F cisminin üzerindeki vektörlerin oluşturduğu kümeye “V” diyelim. V’nin bir vektör uzayı olabilmesi için aşağıdaki tüm aksiyomları vektör toplamına ve vektör skaler çarpımına göre sağlaması gerekir.
- V’nin elemanı olan tüm v ve w vektörleri için, v +v w = w +v v doğru olmalıdır. Farklı bir deyişle, vektör toplama işleminin değişme özelliği uygulanabilir olmalıdır.
- V’nin elemanı olan tüm v, w ve u vektörleri için, v +v (w +v u) = (v +v w) +v u doğru olmalıdır. Farklı bir deyişle, vektör toplama işleminin birleşme özelliği uygulanabilir olmalıdır.
- V’nin elemanı olan tüm v vektörü için, v +v 0 = v değerini veren “0 vektörü” V kümesinin elemanı olmalıdır. Farklı bir deyişle, vektör toplama işleminin etkisiz elemanı V’de bulunmalıdır. Ayrıca değişme özelliğinden dolayı, sağ ve sol etkisiz elemanları aynı olacaktır.
- V’nin elemanı olan tüm v vektörü için, v +v (-v) = 0 değerini veren “-v” V kümesinin elemanı olmalıdır. Farklı bir deyişle, V içindeki her vektörün toplama işlemine göre tersi yine V kümesinin içinde bulunmalıdır. Ayrıca yine değişme özelliğinden dolayı herhangi bir v vektörü için sağ ve sol ters elemanları aynı olacaktır.
- V’nin elemanı olan tüm v vektörü için, 1F .v v = v değerini veren “1F” F kümesinin çarpma işlemine göre etkisiz elemanı olmalıdır. Ayrıca değişme özelliğinden dolayı, sağ ve sol etkisiz elemanları aynı olacaktır.
- V’nin elemanı olan tüm v vektörü ve F’in elemanı olan tüm a ve b değerleri için, (a + b) .v v = (a +v v) .v (b +v v) doğru olmalıdır. Farklı bir deyişle, cisim üzerinde kullanılan toplama işlemi vektör skaler çarpımına göre dağılma özelliğine sahip olmalıdır.
- V’nin elemanı olan tüm v ve w vektörleri F’in elemanı olan tüm a değerleri için, a .v (v +v w) = (a .v v) +v (a .v w) doğru olmalıdır. Farklı bir deyişle cisimden aldığımız herhangi bir değer ile vektör toplamlarının skaler çarpımlarında, vektör skaler çarpımları vektör toplamları üzerine dağılma özelliğine sahip olmalı.
- V’nin elemanı olan tüm v vektörü F’in elemanı olan tüm a değerleri için,(ab) .v v = a .v (b .v v) doğru olmalıdır.
Bu aksiyomlardan ilk 4 aksiyom bize (V, +)’nın abelyen grup olduğunu gösterir ve hiçbir vektör uzay boş küme olamaz çünkü her zaman 0 vektörünü içinde bulundurur.
Alt Uzay Nedir?
Herhangi bir cisim üzerinde “V” vektör uzayının altkümesi olan bir “W” kümesi alalım. Eğer;
- Sıfır vektörü W’nun içinde bulunuyorsa,
- W vektör toplamına göre kapalıysa (W’dan alınan herhangi iki vektörün toplamları da W’da bulunuyorsa),
- W skaler çarpıma göre kapalıysa (cisimden herhangi bir c değeri ve W’dan herhangi bir vektörün skaler çarpımı W’da bulunuyorsa)
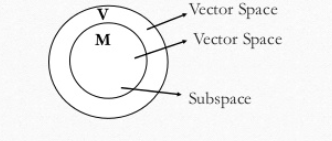

Bu alt küme alt uzay olarak adlandırılır. Her alt uzay aynı zamanda vektör uzaydır.
Alt Uzayların Toplamları
Herhangi bir cisim üzerinde “V” vektör uzayının alt kümesi olan W1 ve W2 kümelerini alalım. Bu iki kümenin toplamları alt uzayların toplamı olarak adlandırılır. W1’den seçeceğimiz herhangi bir v vektörü ve W2’den seçeceğimiz herhangi bir w vektörü için alt uzayların toplamının oluşturduğu kümenin gösterimi aşağıdaki gibi olur.
W1 + W2 = {v +w | v ∈ W1 , w ∈ W2}
Alt uzayların toplamı kendi başına da ayrıca bir alt uzay ve alt uzay olduğu için de vektör uzaydır.
Toplamdan elde ettiğimiz alt uzayın bütün vektörleri sadece birer toplanan alt uzayların vektörlerinden elde edilebiliyorsa; örneğin, 3 boyutlu düzlemde u(0, 0, 5) vektörünü topladığımız iki alt uzaydan sadece v(0, 0, 2) ve w(0, 0, 3) vektörleriyle elde edebiliyorsak başka herhangi bir v ve w ikilisinin toplamı u(0, 0, 5) vektörünü vermiyorsa bu alt uzay toplamı direkt alt uzay toplamı olarak adlandırılır. Gösterimi ise aşağıdaki gibi olur.
W1 ⊕W2 = {v +w | v ∈ W1 , w ∈ W2}
Alt uzayların toplamı direkt ise alt uzayların kesişim kümesi de sadece sıfır vektörünü içermelidir. Örnek olarak ise tek ve çift fonksiyonların reel sayılar üzerindeki tüm fonksiyonların alt uzayı olması ve kesişimlerinin sadece sıfır vektörü olması düşünülebilir.
Hazırlayan: Barış Şahin
Editör: Ögetay Kayalı
Referanslar
1. Terry Tao’s Notes on Linear Algebra: https://terrytao.files.wordpress.com/2016/12/linear-algebra-notes.pdf
2. Sheldon Axler, Linear Algebra Done Right Third Edition
3. Kenneth Hoffman & Ray Kunze, Linear Algebra Second Edition
Kapak Görseli: https://www.edx.org/course/math-of-data-science-linear-algebra
