Küresel Koordinat Sistemi - Eşitlikler ve Dönüşümler

- Özgün
Küresel koordinat sistemi; üç boyutlu uzaydaki bir noktayı orijine olan uzaklık r ile birbirine dik kutup açısı θ ve azimut açısı φ ile tanımlayan koordinat sistemidir. Fizikte özellikle küresel yapılar üzerinde çalışıldığında, kartezyen koordinat sistemi olan (x,y,z) yerine, küresel koordinatlar olan (r, θ , φ) tercih etmek, çözümleri birçok durumda oldukça basite indirger.
Örneğin bir parametrenin merkezden yüzeye olan değişimini, kartezyen koordinatlarda ifade etmek için değişen üç parametre (x,y,z) kullanmamız gerekirken, kutupsal koordinatlarda sadece r'nin değişimini incelemek yeterlidir.
Mesela Güneş'in merkezinden yüzeyine olan yoğunluk gradyenti kutupsal koordinatlarla kolayca hesaplanabilir. Çünkü sadece merkezden yüzeye olan uzaklık olan r'nin bir fonksiyonudur, θ ve φ açılarına göre değişmez. Böylelikle problem üç değişken yerine, tek değişkenle daha basit bir şekilde incelenebilir.
Bu nedenle yeri geldiğinde kartezyen koordinatlardan, kutupsal koordinatlara dönüşüm yapmak gerekir. Keza bazı durumlarda tersi de geçerli olabilir. Hatta bir problemin içerisinde iki yönde de dönüşüm yapmayı gerektiren zamanlar olabilir.
Küresel Koordinat Sistemi
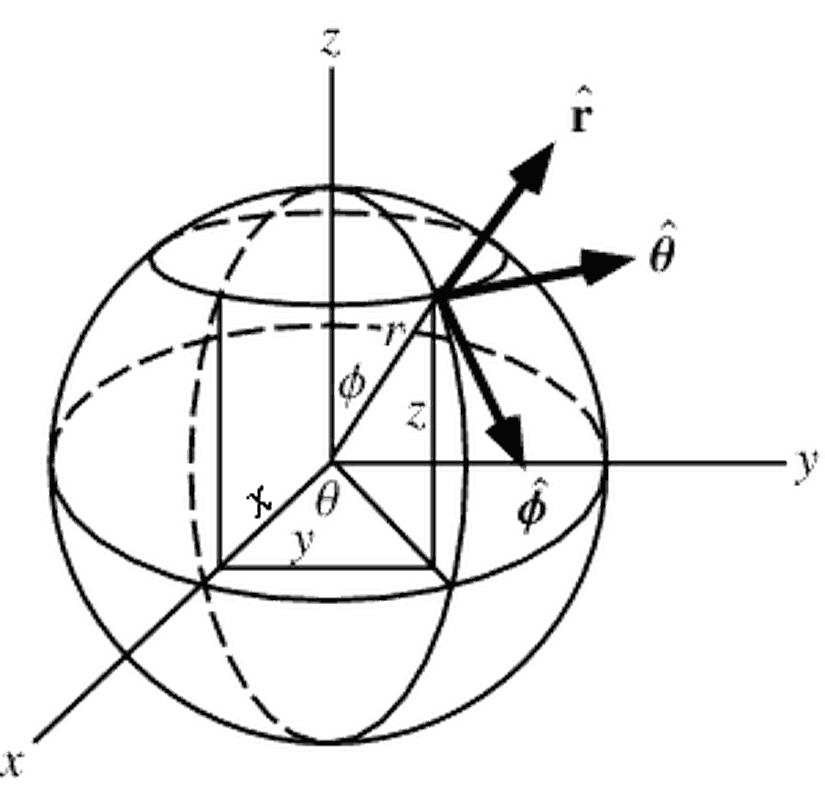
Kullanılan kaynağa göre θ ile φ yer değiştirilmiş olarak gösterilebilir. Burada olası bir kafa karışıklığını önlemek için bu açıların neyi tanımladığını bilmekte fayda var. Biz burada kutup açısını (polar, zenit açısını) φ ile (z-ekseninden yapılan açı), azimut açısını da θ ile göstereceğiz (x-ekseninden yapılan açı).
| Sıralama | Notasyon | Referans |
| (radyal, azimutal, polar) | (r, θ, φ) | Bu yazıda bu notasyon kullanılmaktadır. |
| (radyal, azimutal, polar) | (ρ, θ, φ) | Apostol (1969, p.95), Anton (1984, p. 859), Beyer (1987, p. 212) |
| (radyal, polar, azimutal) | (r, θ, φ) | ISO 31-11, Misner et al. (1973, p. 205) |
| (radyal, polar, azimutal) | (r, θ, φ) | Arfken (1985, p.102) |
| (radyal, polar, azimutal) | (r, θ, ψ) | Moon and Spencer (1988, p. 24) |
| (radyal, polar, azimutal) | (r, ν, φ) | Korn and Korn (1968, p. 60), Bronshtein et al. (2004, pp. 209-210) |
| (radyal, polar, azimutal) | (ρ, φ, θ) | Zwillinger (1996, pp. 297-299) |
Zenit açısı 0° ≤ φ ≤ 180° aralığında yer alır. Azimut açısı ise 0° ≤ θ ≤ 360° arasındadır. Böylelikle birbirine dik iki eksende ifade edilen kutup açılarıyla bir kürenin tüm noktaları tanımlanmış olur. Bunu şöyle düşünebiliriz: θ açısını 0'dan 360'a kadar döndürelim. Bu durumda yukarıdaki görsele bakacak olursak xy-düzlemindeki çemberi çizmiş olduğumuzu görürüz. Şimdi bu çember φ açısı boyunca 180 derece çevirerek kapladığı hacmi hayal edelim. Bu bir tam küredir!
Burada zenit açısıyla ilgili bir konuya dikkat çekmekte yarar var. Dünya üzerinde tanımladığımız enlemler de φ=90-δ ile tanımlanır. Burada δ enlemi belirtir. Eğer φ=0 olduğu durumu inceleyecek olursak, bunun görselde tam tepe noktasına denk geldiğini görürüz. Burası Dünya üzerinde kuzey kutup noktasıdır ve enlemi δ=90'dır. Benzer şekilde enlemi δ=0 olan ekvator için φ=90 derecedir.
Küresel Koordinatlarda Dönüşümler
Kartezyen Koordinatlardan Küresel Koordinatlara Dönüşüm
Kartezyen koordinatlardan küresel koordinatlara dönüşüm için aşağıdaki eşitlikleri kullanırız. Burada r sıfırdan sonsuza, θ 0'dan 360'a (ya da 0'dan 2π'ye) φ ise 0'dan 180'e (ya da 0'dan π'ye) tanımlıdır.
Küresel koordinatlar, kartezyen koordinatlar cinsinden aşağıdaki gibi tanımlanır.
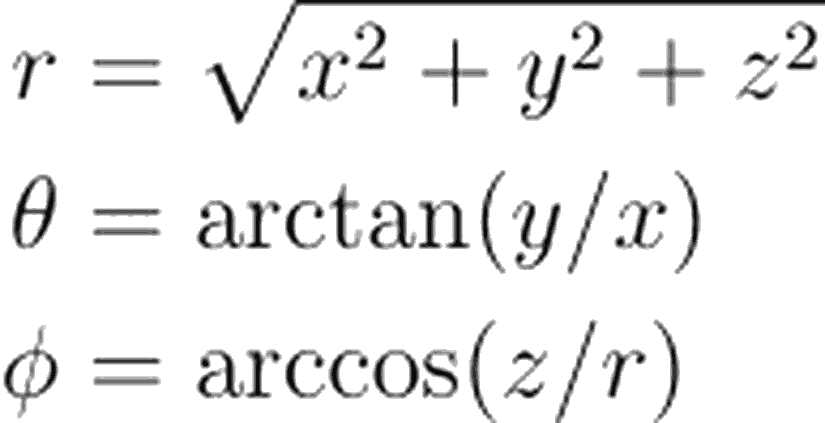
Küresel Koordinatlardan Kartezyen Koordinatlara Dönüşüm
Kartezyen koordinatlar, küresel koordinatlar cinsinden aşağıdaki gibi tanımlanır.
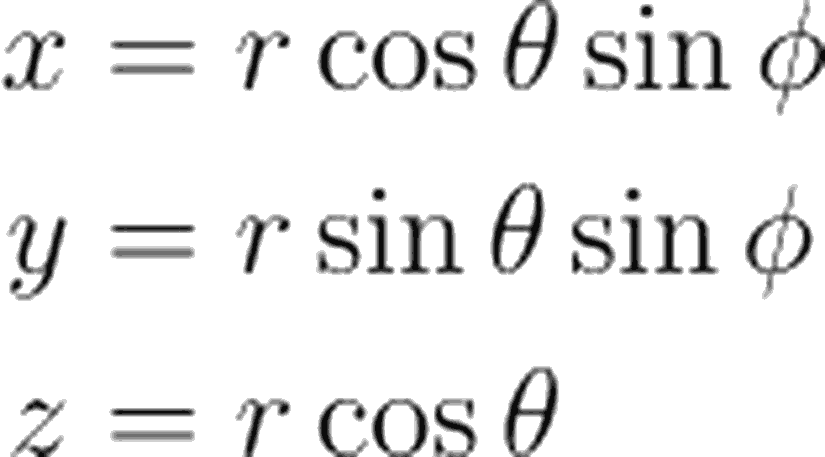
Dolayısıyla kartezyen koordinat sisteminden, küresel koordinat sistemine dönüşüm (ya da tam tersi) bu iki ifade kullanılarak kolaylıkla yapılabilir. Eğer elinizde kartezyen koordinatlar var ve kutupsal koordinatlardaki karşılığını istiyorsanız birinci dönüşüm setini, kutupsal var ama kartezyene dönüşüm istiyorsanız da ikinci dönüşüm setini kullanmanız gerekir.
Küresel Koordinat Sistemi Özellikleri
Küresel koordinat sisteminde çizgi elemanı (line element)

Küresel koordinat sisteminde alan elemanı (area element)
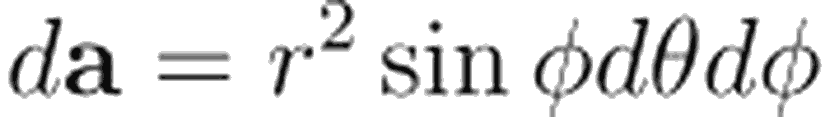
Küresel koordinat sisteminde hacim elemanı (volume element)
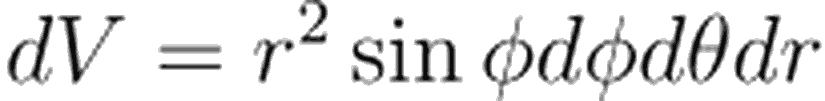
Küresel koordinat sisteminde yarıçap vektörü (radius vector)
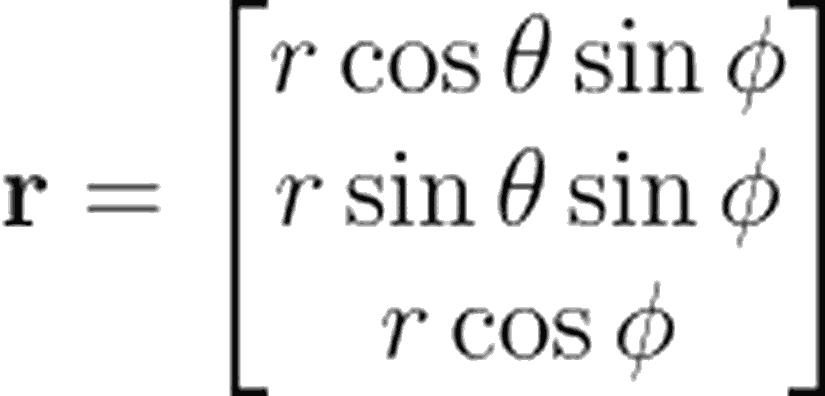
Birim vektörler

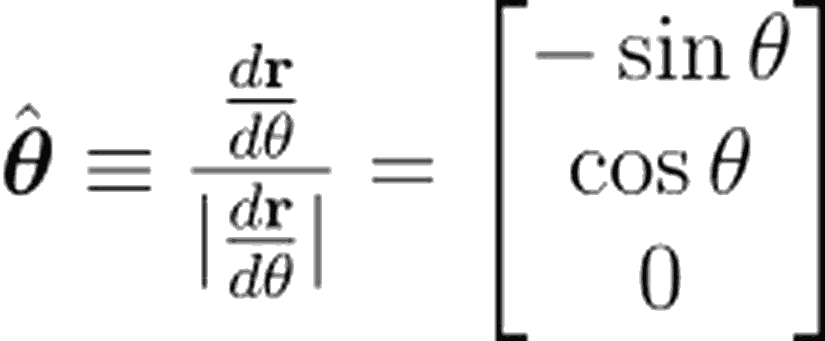

Birim vektörlerin türevleri
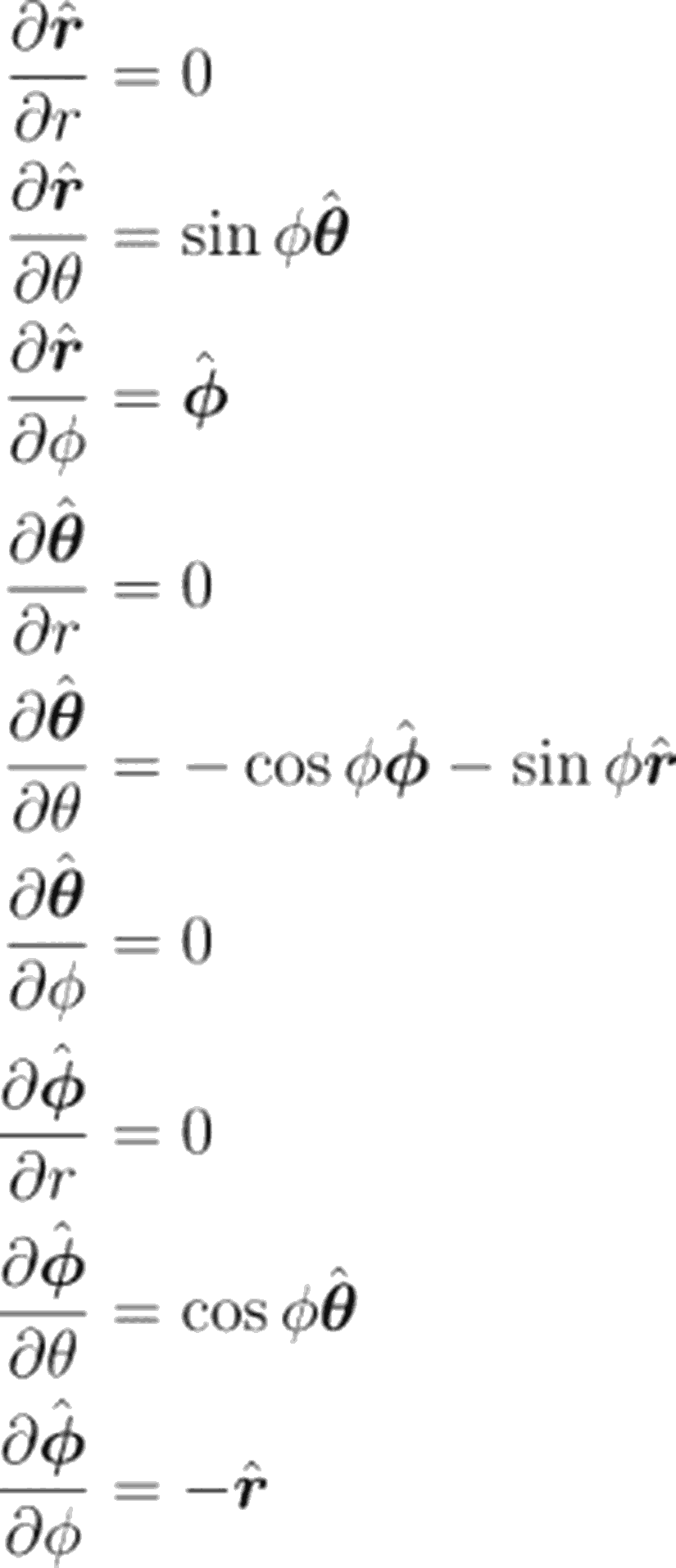
Küresel Koordinatlarda Gradyent

Sorularınız için: Rasyonalist forum.
Hazırlayan: Ögetay Kayalı
Referanslar
1. Mathworld Wolfram, "Spherical Coordinates", <http://mathworld.wolfram.com/SphericalCoordinates.html>
Kapak Görseli: Heisenberg1234 - http://heisenberg1234.deviantart.com/art/Abstract-sphere-wallpaper-374498682
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 18/04/2024 22:06:14 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12940
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.


