Kuantum mekaniği yazı dizimizin önceki yazılarında, zamandan bağımsız Schrödinger denklemini türetmiştik ve ardından da, dalga fonksiyonunun normalizasyonunu incelemiştik. Bu yazımızda ise, normalizasyon konseptinin karşımıza çıkarttığı bir konseptten, olasılık akımından bahsedeceğiz.
Yazımıza geçmeden önce ufak bir hatırlatma yapalım, bu yazımızın daha iyi anlaşılması adına, öncelikle bahsettiğimiz bu iki yazının okunması önem teşkil etmektedir.
Normalizasyon hakkında konuştuğumuz yazımızda, normalizasyonun zamana göre değişimini de incelemiştik. Bu incelemeye, normalizasyonun zamana göre türevini alarak başlamıştık.
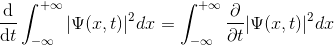
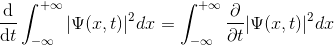
İntegralin içerisine aldığımız türev ifadesini, çarpım türevi kuralına göre açmış, ardından da zamana bağlı Schrödinger denkleminden faydalanarak, bu denklemi düzenlemiştik. Tüm bu işlemlerin sonucunda, elde ettiğimiz ifade
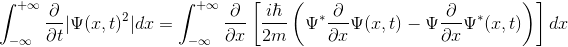
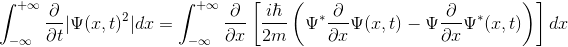
şeklindeydi. İntegralin içerisindeki ifadelerin birbirine eşit olması gerekir. Şimdi, ifadeyi istediğimiz şekle sokmak adına, eşitliğin sol tarafındaki ifadede bulunan türev operatörünü dışarıya alalım ve sağ tarafa da ufak bir düzenleme yapalım.
Olasılık Akımı
Bahsettiğimiz düzenlemeler sonunda;
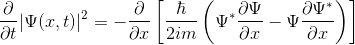
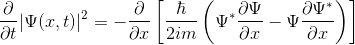
elde etmiş oluruz. Bu eşitliğin sağ tarafında bulunan ifade, olasılık akımı ( j(x,t) ) olarak tanımlanır. Yani:


şeklindedir. Bu da demek olur ki:
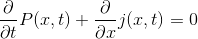
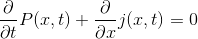
Bu ifade, yazı dizimizin ilerleyen yazılarında oldukça büyük önem arz edeceğinden, fiziksel anlamını sindirmek son derece önemlidir. Düşünecek olursak, denklemin bize verdiği bilgi şöyle özetlenebilir:
Parçacığın herhangi bir noktada bulunma olasılığının zamana göre değişme miktarı ile parçacığın hareketi (ya da parçacığı ifade eden olasılık dalgasının akısı) birbiriyle ilişkilidir.
Denklemimizde değişiklik yapma sebebimiz, fiziğin farklı alanlarındaki korunum yasalarıyla ilişki kurmaktı. Bu benzerliği kurmak adına, ifadenin tüm uzayda integralini alalım.
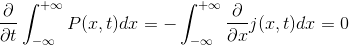
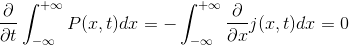
Buna oldukça benzer bir ifade; karşımıza klasik elektrodinamikte, yük korunumunda çıkar. P(x,t), yük yoğunluğu; j(x,t) ise yük akışı anlamına gelir.
İlerleyen yazılarımızda, olasılık akımı kavramını kullanarak tünelleme başta olmak üzere pek çok farklı kuantum mekaniksel konsepti inceleyeceğiz.
Ege Can KARANFİL
Referanslar
1. Stephen Gasiorowicz, Quantum Physics, 3rd Edition
2. Prof. Dr. Osman Yılmaz, Quantum Physics ders notları
3. David J. Griffiths, Introduction to Quantum Mechanics, 2nd edition
4. Prof. Dr. Gürsevil TURAN, Quantum Physics ders notları
Kapak Görseli
1. https://online.stanford.edu/courses/soe-yeeqmse01-quantum-mechanics-scientists-and-engineers
