Dalga denkleminin özelliklerini incelediğimiz yazı dizimizin bu yazısında, dalga denkleminin en önemli özelliklerinden birisi olan normalizasyonu ve zaman ile olan ilişkisini inceleyeceğiz.
Dalga denkleminin (Ψ) mutlak karesinin ( |Ψ|²) bizlere, parcacığın bir noktadaki ya da bir bölgedeki bulunma olasılığını verdiğini söylemiştik. Örneğin, parcacığın a ile b noktaları arasında bulunma olasığını yazacak olursak:
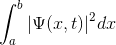
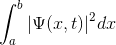
şeklinde ifade ederiz. Biliyoruz ki olasılık tanımı gereği 0 ile 1 arasındadır ve mümkün olan tüm olasılıkların toplamı 1’e eşittir. Öyleyse, benzeri bir ifadeyi, |Ψ|² için de yazabiliriz. Yani, a ile b arasında değil de tüm uzayda bulunma olasılığını yazarsak, bunun 1’e eşit olmasını bekleriz. Bunu matematiksel olarak ifade edecek olursak,
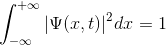
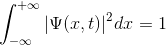
İşte herhangi bir dalga fonksiyonuna bu işlemi uyguladığımızda, onu normalize etmiş oluruz. Peki verilen bir dalga fonksiyonuna, herhangi bir t0 anında normalizasyon uyguladığımızı varsayalım. Bu dalga fonksiyonu, t>t0 anında da bu özelliğini koruyacak mı? Yani, başka bir deyişle zaman, normalize edilmiş dalga fonksiyonumuzu etkiler mi?
Normalizasyonun Zamana Göre Değişimi
Matematik, kuantum mekaniğindeki en önemli gücümüz. Öyleyse, bu gücümüzü kullanarak bu soruya cevap verebilmeliyiz!
Biliyoruz ki eğer bir fonksiyonun zamana göre türevini alırsak, o fonksiyonun zamana göre nasıl değiştiğini bulabiliriz. Eğer ki bu işlemin sonucu, her zaman 0 sonucunu veriyorsa, bu demek olur ki fonksiyon zamana göre değişmemektedir. Öyleyse, biz de yukarıdaki normalizasyon işlemimizin zaman göre türevini alalım ve neler oluyor bir bakalım.
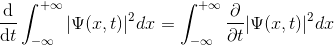
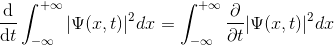
Öncelikle, ![]()
![]()
![]()
![]()
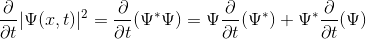
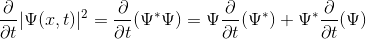
Şimdi, zamana bağlı Schrödinger dalga denklemini hatırlayalım.
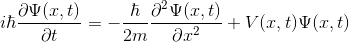
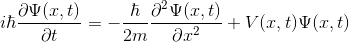
Bu ifadeyi biraz düzenlersek ve zamana bağlı türevi yalnız bırakırsak:
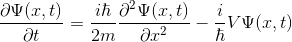
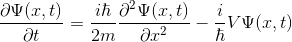
olur. Benzer şekilde, dalga denkleminin kompleks eşleniği de:
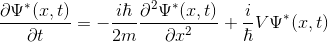
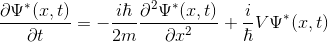
şeklinde yazılır. Bu iki denklemi kullanırsak:
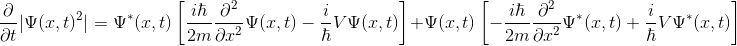
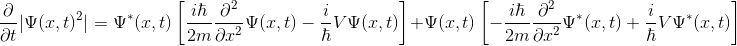
haline gelir. Eşitliğin sağ tarafını düzenlersek:
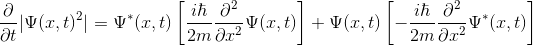
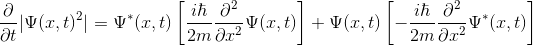
şeklinde yazılabilir. Bu denklemi de düzenlersek:
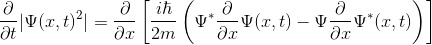
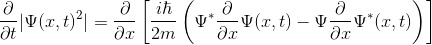
elde ederiz. Yukarıdaki iki denklem ile biraz zaman geçirmek ve birbirlerine eşit olduklarını görmek herkes için iyi olabilir. O yüzden sizlere bunu şiddetle öneriyoruz. Şimdi bu denklemi integralimizin içerisine yerleştirelim.
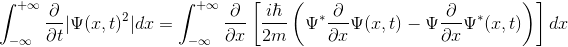
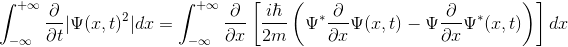
Kalkülüsün temel teoremini kullanarak, eşitliğin sağ tarafının, yine eşitliğin sağ tarafında köşeli parantez içerisinde bulunan değere eşit olduğunu söyleyebiliriz. Öyleyse,
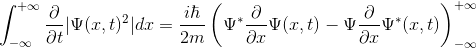
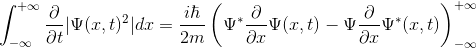
olur. Dalga denklemi ![]()
![]()
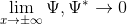
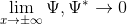
şeklindedir. Öyleyse:
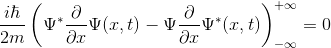
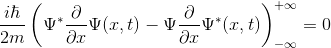
olur. Yani:
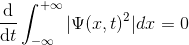
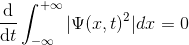
demektir. Bu da demek oluyor ki ne kadar zaman geçerse geçsin, normalize edilmiş olan dalga denklemi, bu özelliğini asla kaybetmez. Başka bir deyişle, verilen dalga fonksiyonunu bir kere normalize ettik mi, o fonksiyon sonsuza dek normalize kalır.
Dalga denkleminin özellikleri hakkında konuştuğumuz bu yazımız eğer aklınızda, “yahu peki bu dalga denklemi nasıl çözülüyor?” sorusunu oluşturduysa, dalga denklemini küresel koordinatlarda çözdüğümüz yazımıza bakabilirsiniz.
Hazırlayan: Ege Can Karanfil
Referanslar
1. David J. Griffiths, Introduction to Quantum Mechanics, 2nd edition
2. Prof. Dr. Gürsevil TURAN, Quantum Physics ders notları
Kapak Görseli
1. https://online.stanford.edu/courses/soe-yeeqmse01-quantum-mechanics-sc
