Kuantum Mekaniği: Lineer Vektör Uzayları

- Özgün
Genel fizikte vektörlerle tanışmıştık. Onlar bizim için yönü ve büyüklüğü olan, yazarken üzerine bir ok işareti çizdiğimiz niceliklerdi. Örneğin hız, momentum ya da ivme vektörel niceliklerdi. Bunlarla ilgili bazı tuhaf gelen kurallar tanımlamış ve bunların vektör cebiri altında işlendiğini söylemiştik. Tuhaf diyoruz çünkü neden bu tür kurallar vermiş olduğumuzu biraz garipsemiş olabilirsiniz.
Örneğin A ve Bbirer vektörse A+B=B+A demiştik (üzerlerine ok işareti koymak yerine vektörleri kalın harflerle göstereceğiz). Bu zaten sezgilerimizin bize söylediği bir şeydir, çünkü şu zamana kadar karşımıza çıkan matematikte yaptığımız işlemler 3+5=5+3 gibi sezgisel işlemlerdi. Keza q gibi bir skalerle çarpma işleminde q(A+B)=qA+qB oluyordu. Bunların hepsi sezgilerimizle uyumludur, birazdan paylaşacağımız detayların da sezgilerimizle uyumlu olduğunu göreceksiniz. Fakat "bunları zaten biliyoruz", "ne var ki bunda", "neden bunları anlatıyorsun" diye düşünmemenizi ve nelerin bu kurallara uyduğunu anlamaya çalışmanızı istiyorum. Nedenini ilerleyip, bazı şeylerin bu şekilde tanımlanmadığını görünce daha iyi anlayacaksınız.
Vektör uzayının tanımlarını incelerken, oklarla gösterdiğimiz bildiğimiz vektörlerle olan ilişkilerine dikkat edin. Bazen öyle vektör uzayı örnekleri göreceksiniz ki, içeriğinin bir büyüklüğe ya da yöne sahip olup olmadığını sezgisel olarak ayırt edemeyeceksiniz. Şu zamana kadar reel sayıların veya kompleks sayıların adını anmadığımıza da dikkat edin.
Dirac notasyonu (Bra-Ket notasyonu)
İlk olarak kuantum mekaniğinde kullandığımız dili tanıyalım. Dirac notasyonu ya da bra-ket notasyonu olarak adlandırdığımız bu gösterimde |V> ya da <V| şeklinde ifadeler göreceksiniz. Burada <V| bra vektörü, |V> ise ket vektörü olarak adlandırılır. Bunların ne anlama geldiğini göreceğiz, fakat şu an için bilmemiz gereken aşağıdaki kurallara uydukları ve işimizi oldukça kolaylaştırdıkları.
Lineer Vektör Uzayları
a,b,... birer skaler olmak üzere |1>, |2>, ... , |V>, |W>, |Z> ... vektörlerinden oluşan bir vektör uzayı için;
- Herhangi V ve W vektörleri için vektör toplamı: |V> + |W>
- Herhangi a skaleri ile V vektörünün çarpımı: a|V>
şeklindedir ve aşağıdaki özellikleri sağlarlar.
- |V> + |W> toplamının ürünü, bu uzayın bir başka ürünüdür (kapalılık özelliği).
- Skaler çarpım, vektörler üzerinde dağılabilirdir: a(|V> + |W>) = a|V> + a|W>
- Skaler çarpım, skalerler üzerinde dağılabilirdir: (a+b)|V> = a|V> + b|V>
- Skaler çarpım, birleşebilirdir (asosiyedir): a(b|V>) = ab|V>
- Toplama, yer değiştirebilir (komütatif): |V> + |W> = |W> + |V>
- Toplama, birleşebilirdir (asosiyedir): |V> + (|W> + |Z>) = (|V> + |W>) + |Z>
- |V> + |0> = |V> eşitliğini sağlayan bir |0> vektörü vardır.
- Her |V> vektörü için |V> + |-V> = |0> eşitliğini sağlayan toplama işlemine göre tersi |-V> bulunur.
Bu noktaya kadar değindiğimiz her şey sezgilerimizin şu zamana kadar bize söyledikleriyle uyumludur, yani pek de yeni bir şey yok gibi görünüyor. Fakat bunların ne anlama geldiklerini yorumlamaya çalışmamız önemli. Bu kurallara uyan bir sistem nasıl bir sistemdir, fiziksel olarak ne anlam ifade eder?
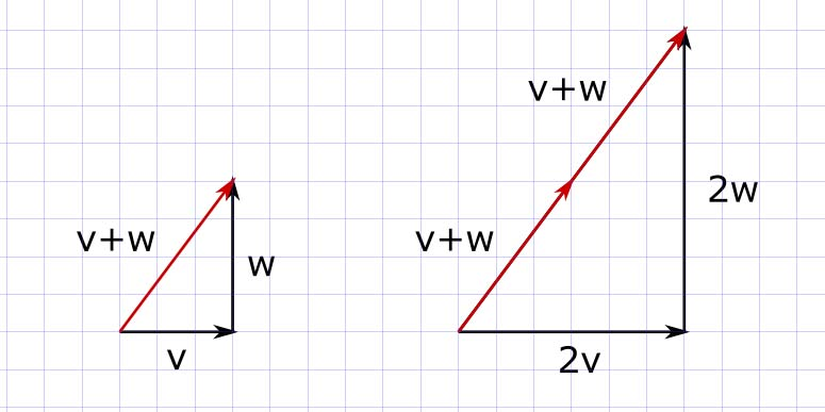
Örneğin ikinci madde (a(|V> + |W>) = a|V> + a|W>) bize ne söylemektedir? Bunun bize söylediği, iki vektörü toplayıp bir skalerle (a) çarpmak, onları ayrı ayrı bu skalerle çarpıp toplamakla aynı sonucu verdiğidir. Aşağıdaki figürde bunu daha net bir şekilde görebiliriz.
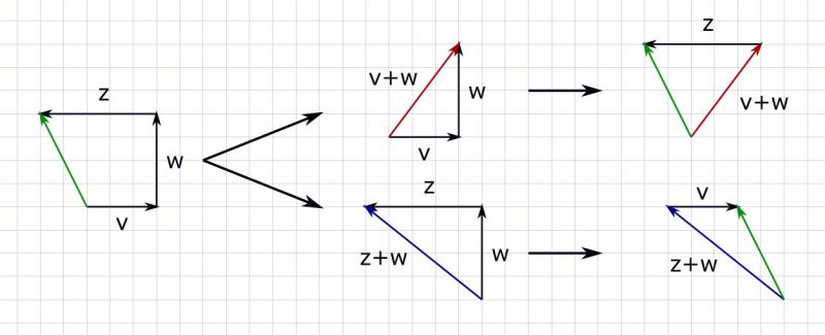
Bir diğer örnek olarak altıncı maddeyi (|V> + (|W> + |Z>) = (|V> + |W>) + |Z>) inceleyelim. En kaba tabiriyle bu madde şunu söyler, üç vektörü toplarken önce hangi iki vektörü topladığınızdan bağımsız olarak, sonuçta aynı vektöre ulaşırsınız. Bunun beşinci maddeyle olan uyumuna dikkat edecek olursak, sadece |V> + (|W> + |Z>) = (|V> + |W>) + |Z> olduğunu değil aynı zamanda |V> + (|Z> + |W>) = (|V> + |Z>) + |W> olacağını da görürüz. Yani toplamanın sırası sonucu değiştirmez, işlem sırasında farklı vektörler oluşsa da sonuç aynıdır. Aşağıdaki figürde bu iki farklı senaryoyu görebiliyoruz, sonuçta oluşan yeşil renkli vektörlerin aynı olduğuna dikkat edin.
Peki burada bahsettiğimiz, vektörler üzerinde onların büyüklüklerini değiştiren (eğer negatifse yönlerini tersine de çeviren) skalerler, bir vektör uzayında ne ifade eder? Biz buna vektör uzayı üzerinde alan (field)diyoruz. Buradaki alan kavramının tanımını anlamak için matematikte neyi ifade ettiğine bakmanızı öneriyorum, bunun detaylarına burada detaylarına girmeyeceğiz. Fakat şunları bilmemiz gerek:
- 0|V>=|0>
- |-V>=-|V>
- |-V>, |V>'nin toplamaya göre tek (unique) tersidir.
- |0> tektir (unique) ve eğer bunun tüm özelliklerini sağlayan bir başka |0'> varsa |0>=|0'> olur.
Bunlar ilk gördüğünüzde çok manalı gelmeyebilir, fakat bunların neden böyle olduğunu anlamamız gerek. Bunun için de böyle olması gerektiğini, önceki aksiyomlara dayanarak ispatlamaya çalışalım. Örneğin dördüncü madde |0>'ın tek (unique) olduğunu söylüyor, peki gerçekten öyle midir? Hatırlayacak olursak,
|V> + |0> = |V>
oluyordu. Bu durumda |0'>gibi bir başka vektörün bu şartı sağlaması durumunda |0>'a eşit olacağını gösterebilmeliyiz.
|V> + |0'> = |V>
dersek aklımıza şu gelebilir: |V> sonuçta herhangi bir vektör, dolayısıyla|0'>veya |0> olabilir. O halde sırasıyla |V> = |0'> ve |V> = |0> yapıp önceki denklemlerde yerine koyarsak aşağıdaki ifadeleri elde ederiz.
|0'> + |0> = |0'>
|0> + |0'> = |0>
Hatırlayacak olursak toplamda komütatiflik özelliğimiz vardı, yani bunların yerleri değişebilir. İkinci denklemde sol tarafta yerleri değiştirirsek görürüz ki,
|0'> + |0> = |0'>
|0> + |0'> = |0>
haline gelirler. O halde |0'> = |0> olmalıdır.
Eğer skalerler reel sayılardan oluşuyorsa uzayımız reel vektör uzayı, eğer kompleks sayılardan oluşuyorsa kompleks vektör uzayı olarak anılır. Dikkat ederseniz henüz bu skalerleri herhangi biriyle sınırlandırmadık.
Buraya kadar bu bra ve ket vektörlerinden bahsederken, bunları üzerine ok işareti çizdiğimiz, büyüklüğü ve yönü olan vektörlerle ilişkilendirdik. Fakat bir vektör uzayının elemanlarının bu büyüklük ve yöne sahip olması gerekmeyebileceğini bilmeli ve aklımızın bir ucunda tutmalıyız. Bunu söylediğimde havada kaldığını biliyorum. Fakat lineer cebirden eğer matrisleri hatırlayacak olursak, bunların da bahsettiğimiz kurallara uyduğunu ama yön ve büyüklük hakkında hiçbir şey söylemediğini görebiliriz. Örneğin 2x2'lik tüm matrisleri barındıran bir küme düşünecek olursak bunların yukarıda tanımladığımız özelliklere uyduğunu görüyoruz. Yani elimizde bir vektör uzayı var, fakat içerdiği elemanlar vektörler gibi yön ve büyüklük bilgisini içermek zorunda değil.
Hazırlayan: Ögetay Kayalı
Referanslar
1. R. Shankar, Principles of Quantum Mechanics, "Mathematical Introduction"
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 26/04/2024 18:22:07 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/13013
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.


