Kuantum Mekaniği: Kare Kuyu Potansiyeli 1

- Özgün
Öncelikle kare kuyu potansiyelimizi tanımlayalım ve görselleştirelim:
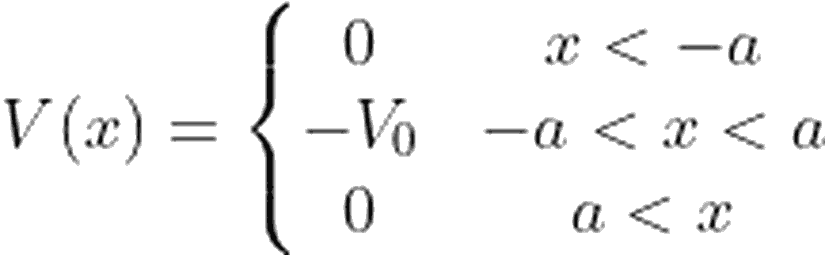
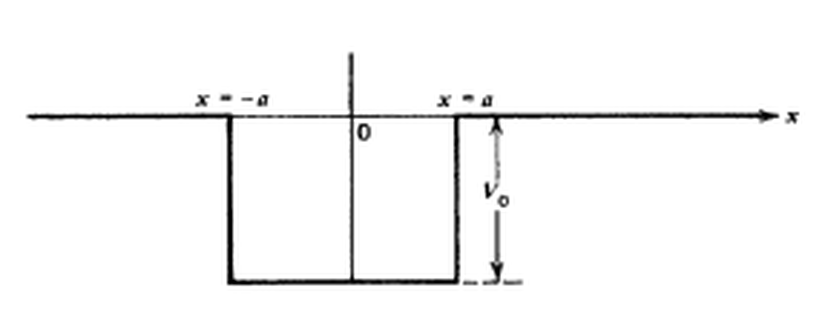
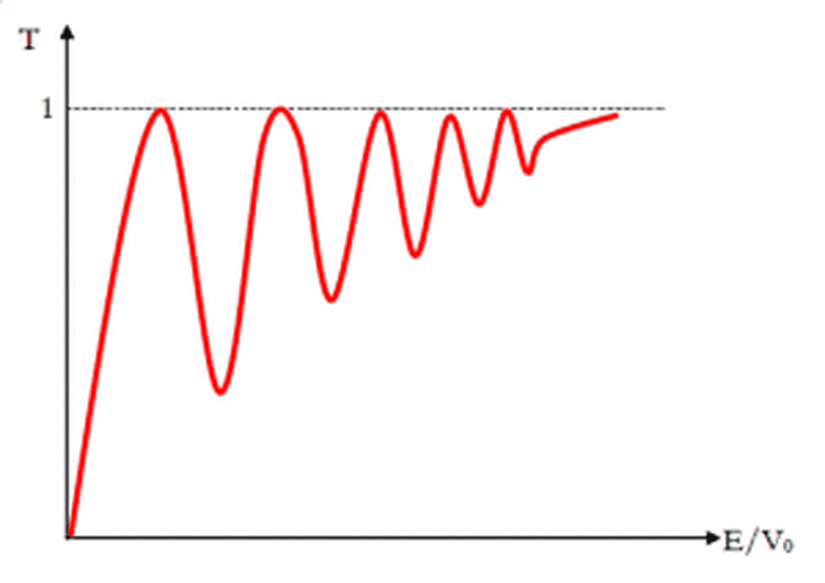
Enerjinin sıfırdan büyük olduğu durum, konsept olarak diğer örneklerle benzerlik gösterir. Değişen potansiyel etkisiyle, dalga fonksiyonunun dalga numarası değişir ve potansiyel değişiminin etkisiyle, gelen dalganın bir kısmı yansır. Bu yansıma, belirli durumlarda maksimum, belirli durumlarda ise minimum değerine ulaşır.
Enerjinin sıfırdan küçük olduğu durum ise E>0 durumundan yeni bir konsepti karşımıza çıkartır. Parçacığın x=-a ve x=a arasındaki bölgedeki davranışı, bağlı durumlar oluşmasını mümkün kılar. Yani, "belirli enerji seviyeleri" karşımıza çıkmış olur. Nükleer fizikte de son derece önemli bir konsept olduğu için, özellikle bu kısım üzerinde epey bir zaman harcayacağız.
Fiziği, matematik dışında bir dil ile ifade etmek çoğu zaman zordur. Lakin konu kuantum mekaniği olduğunda, mesele daha da güç bir hal alır. Her ne kadar sezgisel bir anlayış için bu tarz sözel açıklamalar kritik olsa da; kuantum mekaniğinin matematiği ile uğraşıp kendi içimizde sezgisel bir kavrayış geliştirmemiz çok daha sağlıklıdır.
Bu sebeple, kelimelere daha fazla boğulmadan konsepti matematiksel olarak incelemeye geçmek yerinde olacaktır. Kavraması nispeten daha kolay olduğu için, E>0 durumuyla başlayalım.
Kare Kuyu Potansiyeli E>0 Durumu
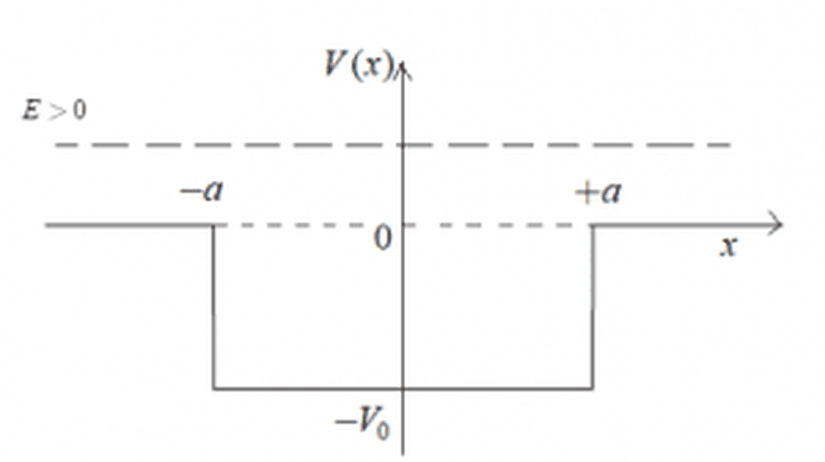
Kuantum mekaniğinde ise, yansıma için elde ettiğimiz değer, yukarıda da bahsettiğimiz gibi sıfırdan farklıdır.
Şimdi, x<-a, -a<x<a ve x>a bölgelerini sırasıyla 1, 2 ve 3 olarak adlandıralım. Hatırlayacağınız gibi, zamandan bağımsız Schrödinger denklemi:
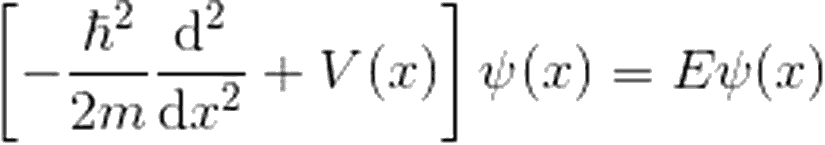
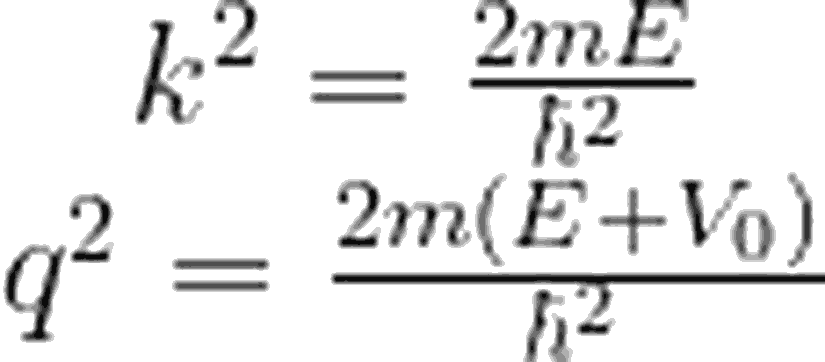
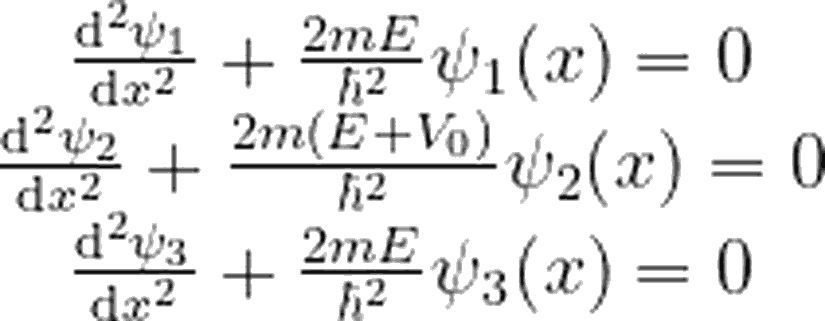
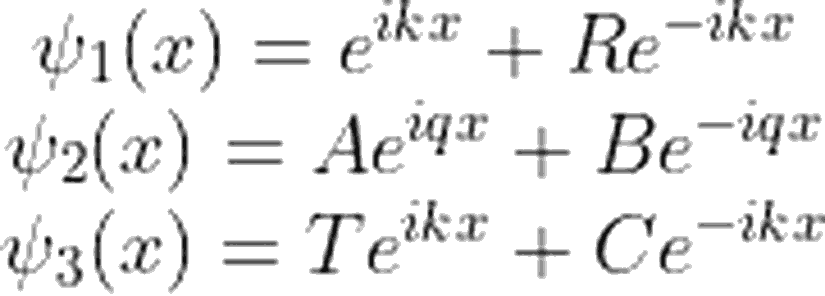
Dalga fonksiyonları için akı tanımını, basamak potansiyeli 1 yazımızda uzunca ele almıştık. Tekrara düşmemek adına, şimdi her bir bölgedeki dalga fonksiyonu için akıları doğrudan yazalım. Bu akıların her bölgedeki toplamı, korunum prensibi gereği birbirine eşit olmalıdır. Öyleyse akı ifadeleri:
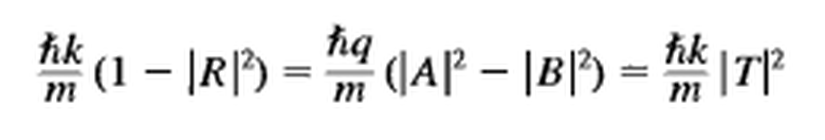
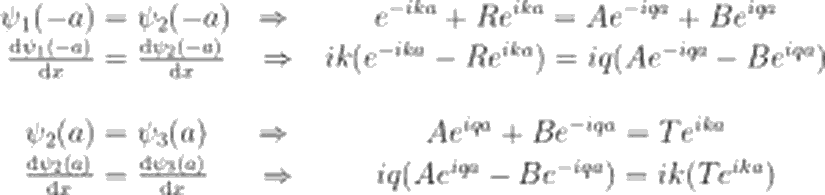
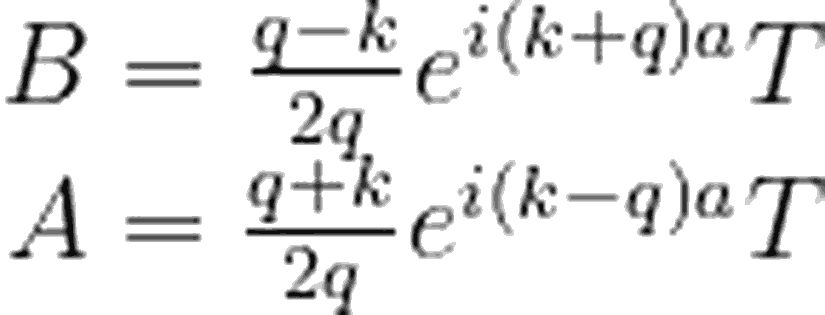
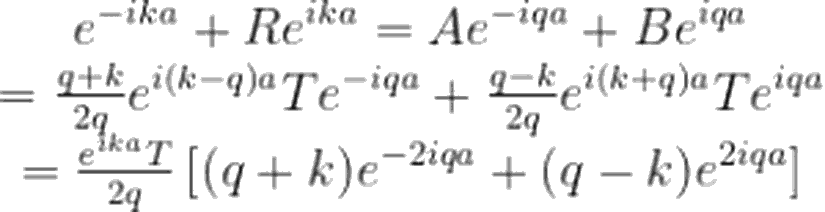
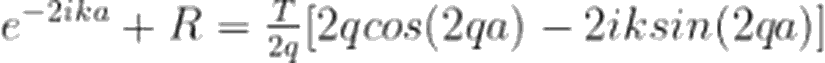
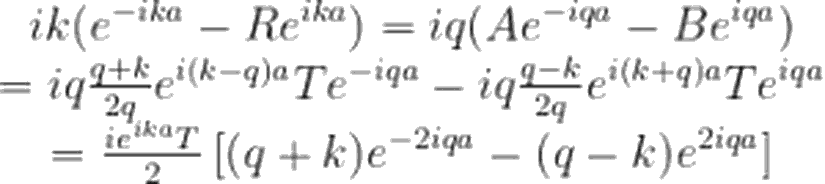
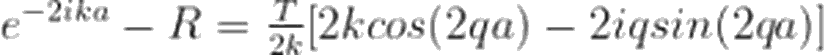
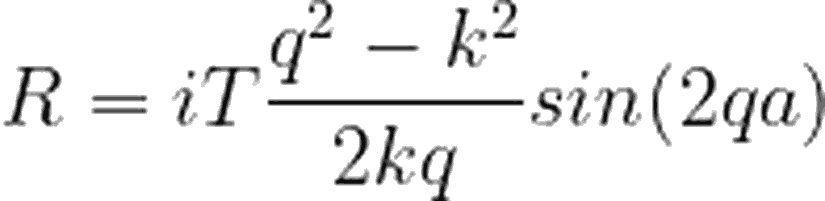
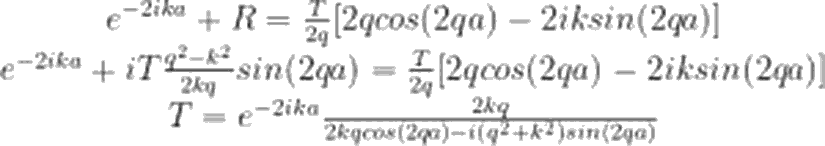
Yinebasamak potansiyeli 1 yazımızda derinlemesine incelediğimiz gibi, |T²| bize, iletim olasılığını verecektir. Yazımızın son kısmında biz de, bulduğumuz bu T ifadesi için |T²|'i hesaplayacağız.
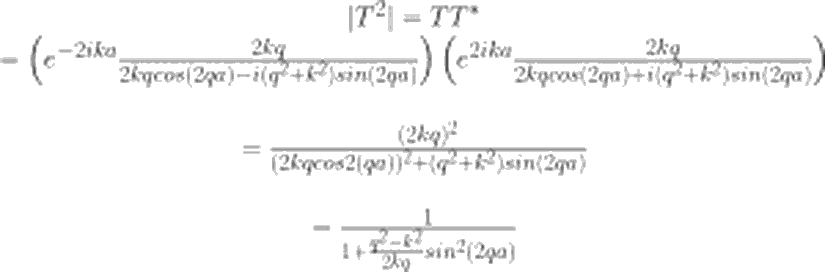
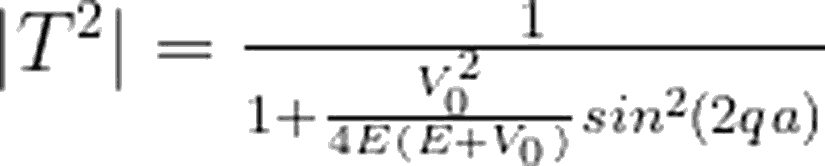
Ege Can KARANFİL
Referanslar
1. Stephen Gasiorowicz, Quantum Physics, 3rd Edition
2. Prof. Dr. Osman Yılmaz, Quantum Physics ders notları
3. David J. Griffiths, Introduction to Quantum Mechanics, 2nd edition
4. Prof. Dr. Gürsevil TURAN, Quantum Physics ders notları
Kapak Görseli
1. https://online.stanford.edu/courses/soe-yeeqmse01-quantum-mechanics-scientists-and-engineers
Ramsauer-Townsend Grafik Referansı
1.https://physicsopenlab.org/2016/08/16/ramsauer-townsend-effect/
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 23/04/2024 19:05:09 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12730
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.



