Elektromanyetik Teori: Gauss Yasası
- Özgün
Herhangi bir elektromanyetik teoriye giriş kitabını elimize aldığımızda, konu akışı çoğunlukla noktasal parçacıkların, Coulomb yasası yardımıyla elektrik alanının bulunmasıyla başlar. Ardından, aynı yasa, integral kalkülüsü kullanılarak 2 ve 3 boyutlu objelere de uygulanır. Lakin, bu işlemler çoğu zaman hayli uzun matematiksel adımlardan oluşur.
Ne mutlu ki, biraz sonra bahsedeceğimiz matematiksel yöntemler yardımıyla, küresel ya da silindirik simetrinin söz konusu olduğu durumlarda, bu uzun adımlardan kurtulmak ve komik sayılabilecek kadar kısa bir sürede aynı sonuca ulaşmak da mümkündür.
Gauss Teoremi
Bu isimler gözünüzü korkutmasın. Fiziğin her alanında olduğu gibi, tüm matematiksel ifadelerimiz, fiziksel bir anlam ifade eder. Gauss teoremi söz konusu olduğunda bu fiziksel anlam, bir noktadan saçılan madde miktarı ile bu noktayı kapsayan herhangi bir yüzeyden çıkan madde miktarı arasındaki ilişkiyle özetlenebilir.Daha anlaşılır olması adına bir örnek ele alalım. Uzayda bir yerde bir ışık kaynağı düşünelim. Bu ışık ne kadar parlaksa, saçılan foton miktarı o kadar fazladır diyebiliriz. Şimdi, bu ışık kaynağını içinde barındıran çeşitli boyda küreler çizelim. Rastgele bir yapıdaki, farklı bir üç boyutlu cisim de çizebilirdik.
Küre seçmemizin sebebi, küresel simetri kavramının, işlerimizi hayli kolaylaştırmasıdır. Kürenin boyutu ne olursa olsun, kürenin toplam yüzey alanından çıkacak olan foton miktarı, ışık kaynağından çıkan foton miktarıyla aynı olacaktır.
Bu kürelerimizin dışında herhangi bir ışık kaynağı varsa, bu ışık kaynağı toplam saçılmada bir değişime yol açmaz. Bunun sebebi de, tahmin edebileceğiniz üzere, kürenin bir yüzeyinden giren fotonların, diğer yüzeyden çıkacak olması ve foton sayısına bir katkı sağlamamasıdır.
İşte! Gauss teoreminin (ya da diverjans teoreminin) söylediği şey de tam olarak budur:
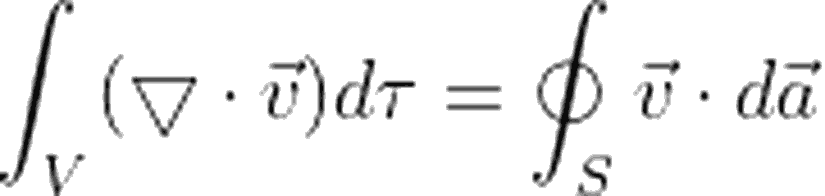
Noktasal Yük ve Gauss Yasası
Az önce noktasal ışık kaynağı ile verdiğimiz örnekte, noktasal ışık kaynağı değil, noktasal bir yük düşünelim. Bu sefer noktasal yükü pek çok küre çizmek yerine, yarı çapı r olan hayali bir kürenin merkezine yerleştirelim.Bu noktasal yükün oluşturduğu elektrik alan vektörlerini inceleyecek olursak, hayali küremizin yüzeyindeki toplam akıyı şu şekilde ifade edebiliriz:
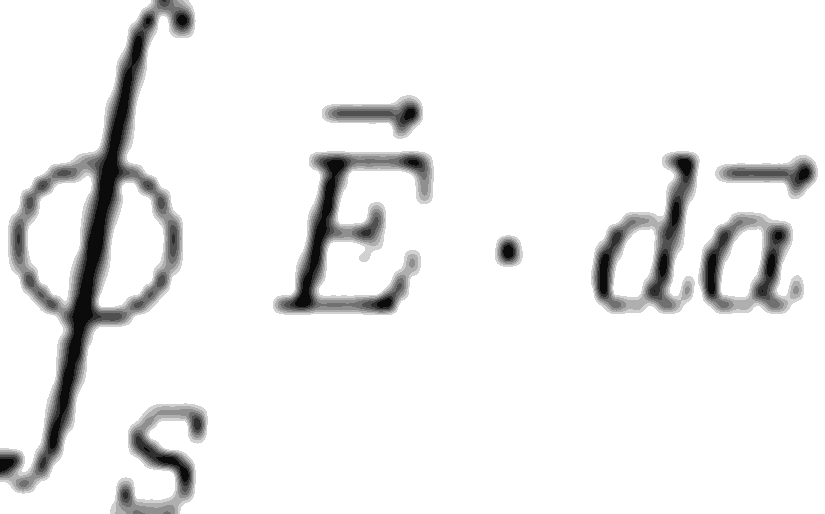
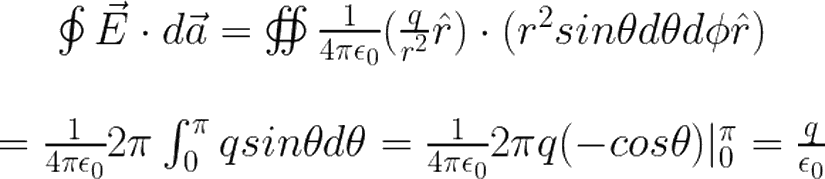
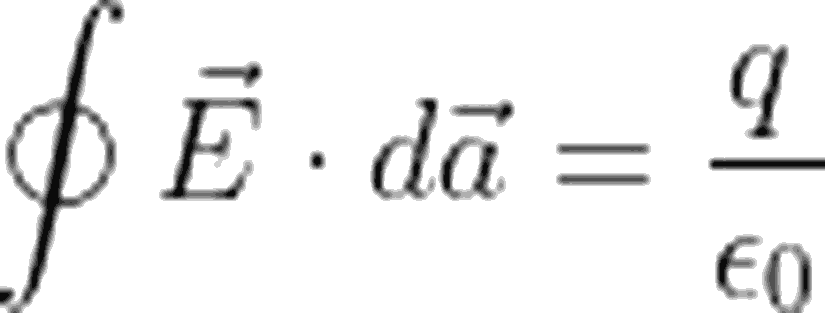
Birden Fazla Yük Durumunda Gauss Yasası
Oluşturduğumuz Gauss yüzeyinin yarıçapından bağımsız olarak, sistemin elektrik alanını bulabildiğimiz için, birden fazla yükün olduğu durumlarda q ifadesi, Gauss yüzeyinin çevrelediği yük miktarını temsil eder. Yani: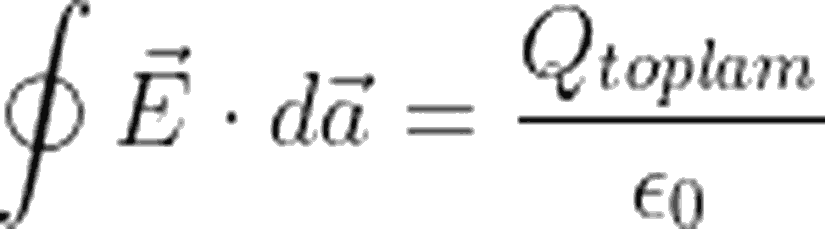
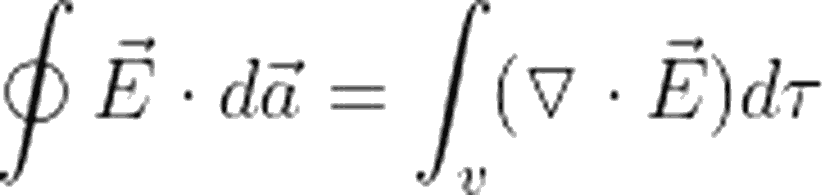
Elektrik Alanın Diverjansı ve Gauss Teoreminin İspatı
Elektrik alanın en genel ifadesini, Coulomb yasasından elde edebiliriz. Hatırlayacak olursanız bu ifade: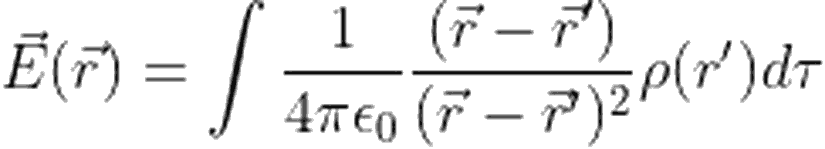
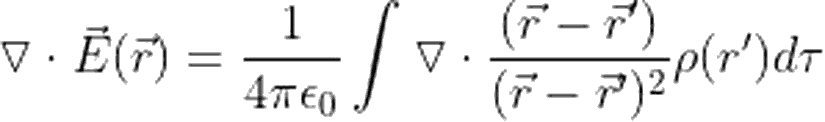
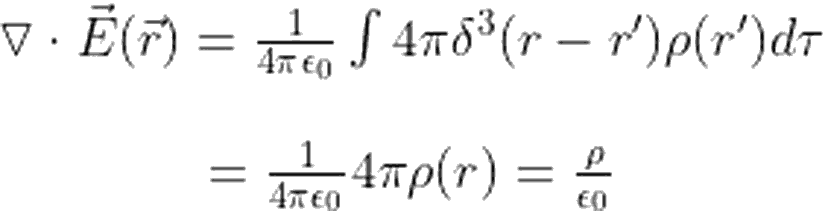
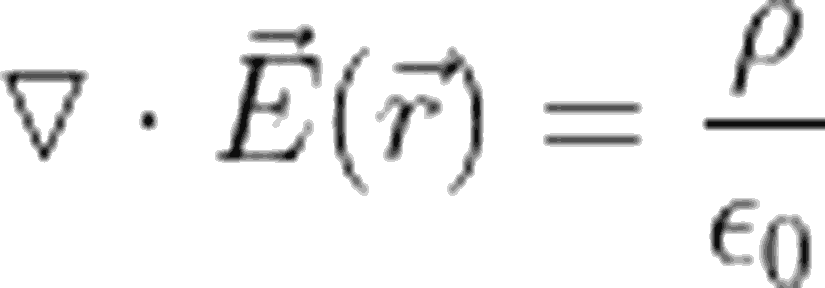
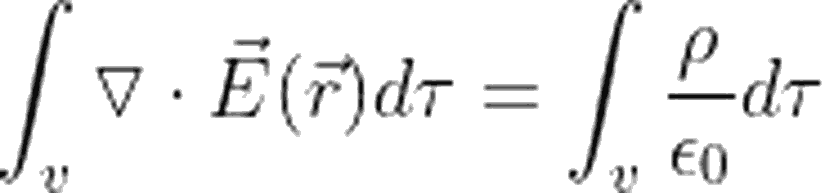
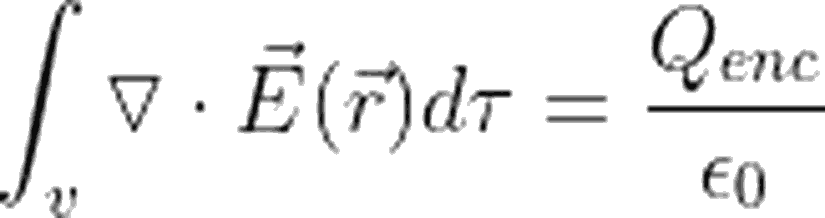
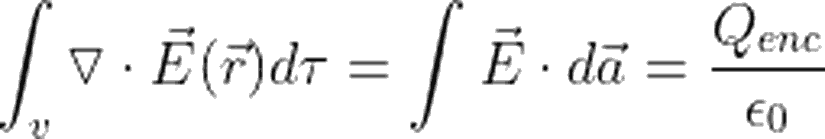
Hazırlayan: Ege Can Karanfil
Editör:Ögetay Kayalı
Referanslar
1. David J. Griffiths, "Introduction to Electrodynamics",4th edition, Pearson, Chapter 2.2
2. Francis B. Hildebrand, "Advanced Calculus for Applications, 1962, Chapter 6
3. Hyperphysics, "Gauss Law", <http://hyperphysics.phy-astr.gsu.edu/hbase/electric/gaulaw.html>
Kapak Görseli:
https://wonderopolis.org/wonder/how-does-a-plasma-ball-work
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 20/04/2024 13:23:50 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12806
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.



