Dirac Delta Fonksiyonu

Dirac delta fonksiyonu, genelleştirilmiş fonksiyon veya dağılımdır ve İngiliz teorik fizikçi Paul Dirac tarafından sunulmuştur. Delta fonksiyonu δ(x); x=0 hariç her yerde değeri sıfır olan, fakat x=0'da sonsuz büyüklüğe sahip olan ve toplam integrali 1'e eşit olan fonksiyondur. Bu fonksiyon, impuls gibi uzun ve dar atımlar gösteren fonksiyonlar için iyi bir yaklaşım sağlar.

Neden Dirac Delta Fonksiyonuna İhtiyaç Duyuyoruz?

Bu durumu öncelikle konsept olarak anlamak adına, basit bir örnekle incelemeye başlayalım. Örneğin, x=0'da noktasal bir q yükümüz bulunsun. Bu yük için yük yoğunluğunu ρ(?)'i nasıl tanımlarız? Bütün yükün x=0 noktasında bulunduğunu biliyoruz. Ancak bunu matematiksel olarak nasıl gösterebiliriz? İşte Dirac delta fonksiyonu bize tam olarak bu noktada yardım etmektedir.

Şimdi, bu örneği matematiksel olarak ifade etmek için, bir vektör fonksiyonu (V) tanımlayalım.

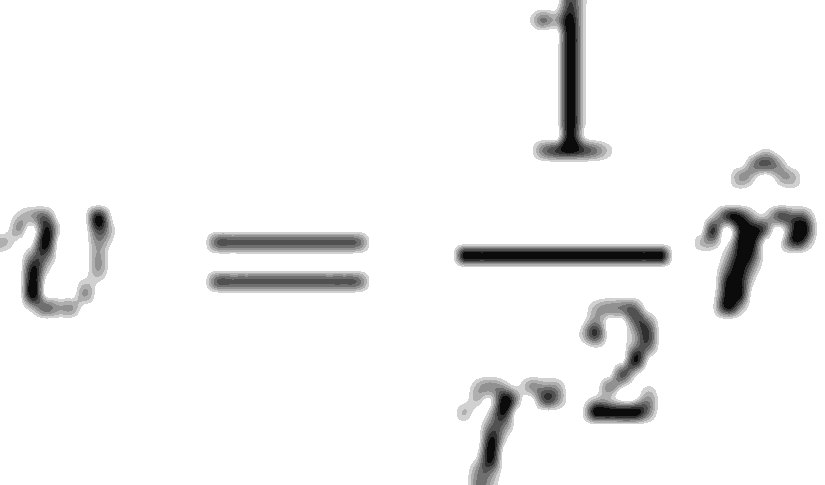
Aslında, bu ifade bir noktasal yükün elektrik alanıyla oldukça benzerdir. Eğer hayal edecek olursanız, bu vektör fonksiyonunun, merkezden dışarı doğru küresel olarak saçıldığını anlayabilirsiniz. Matematik dilinde saçılmak demek diverjans demektir. Öyleyse, küresel koordinatlarda bu ifadenin diverjansını alalım ve ne buluyoruz inceleyelim. Diverjans ifademiz aşağıdaki gibiydi.

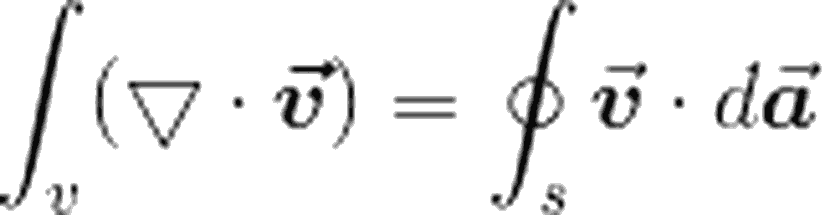
Küresel koordinatlarda diverjans ifadesini ise şu şekilde yazabiliriz:

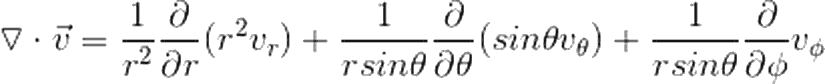
Şimdi, vektör fonksiyonumuzu yerine yazalım.

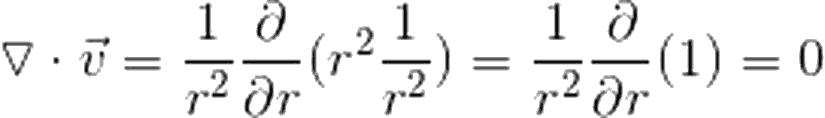
Cevap sıfır! "Dışarı doğru saçılan bir fonksiyonun diverjansı nasıl sıfır olabilir ki?" diye sorabilirsiniz. Bu soruya cevap vermeden önce başka bir şey daha deneyelim. Sonuçta diverjans teoremimizin doğru olduğunu biliyoruz. Öyleyse, bir de o teoremi kullanalım ve bakalım diğer taraf da bize sıfır mı veriyor.

Diverjans ya da Gauss teoremine göre, önce bir kapalı yüzey tanımlamamız gerekiyor. Bu yüzeyi, yarıçapı R olan ve merkezi (0,0,0) noktasında olan bir küre olarak tanımlayalım. Öyleyse:

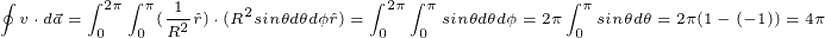
Şimdi de 4π çıktı! Hani Gauss (diverjans) teoremi doğruydu? Biz mi bir yerlerde hata yapıyoruz? Yoksa Gauss teoremi mi yanlış? Nedir bu olan?

Olan şey aslında çok basit. Vektör fonksiyonumuz, r=0 olduğunda sonsuza gidiyor. Bütün karışıklığın sebebi de bu nokta. Eğer ki, diverjansımızı r=0 noktası dışında bir noktada hesaplasaydık, bulacağımız cevap kesinlikle 0 olmalıydı. Çünkü oluşturacağımız hacimin içerisinde bir kaynak olmayacaktı. Hesaplayacağımız yüzey integraline bakacak olursak da, oluşturduğumuz kürenin yarıcapı R ne olursa olsun, çıkan sonucun 4π olacağını görebiliriz. Öyleyse, bu iki sonucu birleştirecek olursak:

V, r=0 noktası hariç her yerde sıfır olmakta. Yüzey integralinden de görebileceğimiz gibi, sonucu r=0'dan gelen katkıyla 4π olmakta.

Dirac Delta Fonksiyonu

?(x) ile ifade edilen Dirac delta fonksiyonu, aşağıdaki gibi tanımlanabilir:

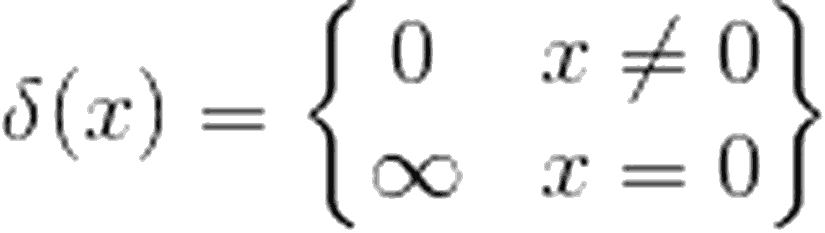
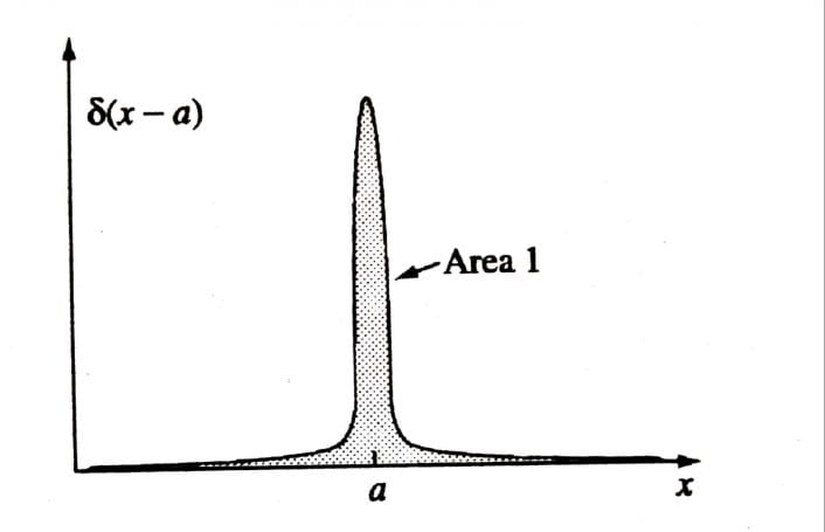
Görsel olarak ifade edecek olursak:

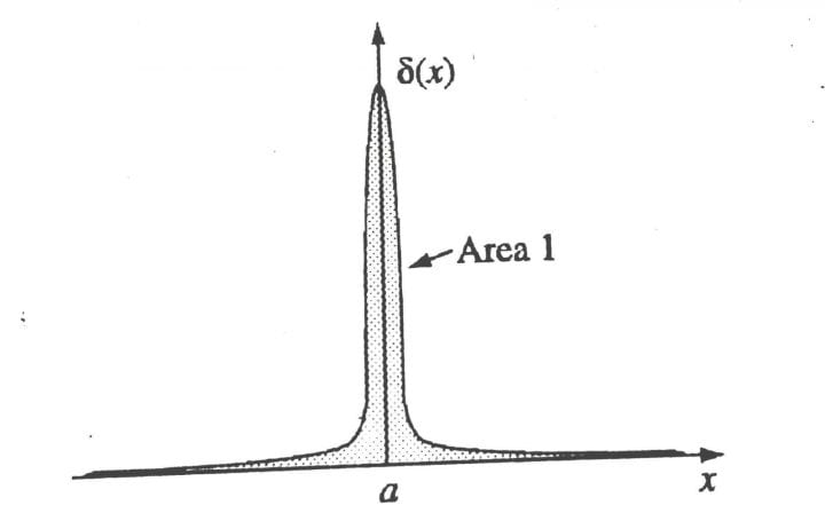
Görselde gördüğümüz sivri yapının alanı 1 olarak tanımlanmıştır. Bu yüzden, -∞ ile +∞ arasında tanımlanan bir integralin sonucu da 1 olmak zorundadır. Yani:

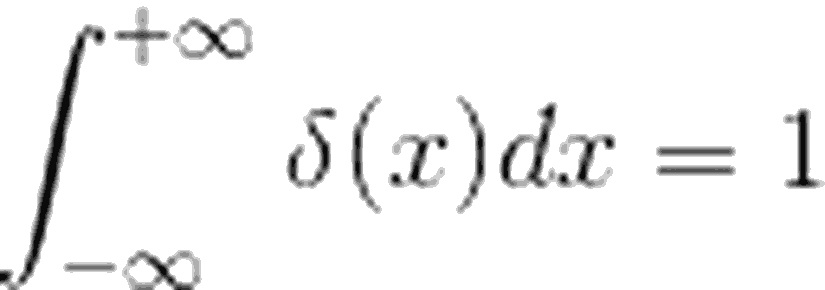
Şimdi, bu ifadenin nasıl kullanıldığını açıklamak adına, f(x) fonksiyonunun ?(x) ile çarpımına bakalım. ?(x), x=0 haricinde 0 sonucunu vereceği için, çarpımı şu şekilde ifade edebiliriz:

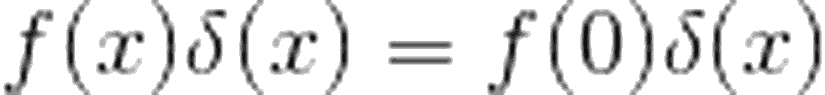
Eğer Kronecker delta ya da Levi-Civita sembolu ile daha önceden tanışmışsanız, Dirac delta fonksiyonunun bu ikisiyle olan benzerliğini görebilirsiniz. Şimdi konudan sapmadan, yukarıdaki çarpımın integralini tanımlayalım:

f(0) sabit olduğundan, diyebiliriz ki:

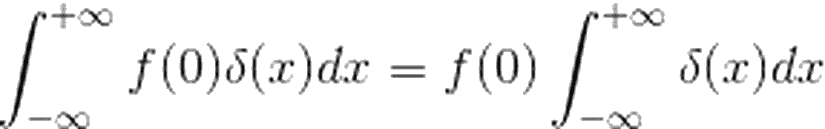
Eşitliğin sağ tarafındaki integrali yukarıda tanımlamıştık. Öyleyse:

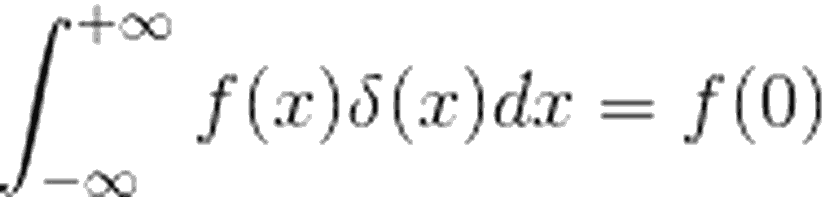
olmuş olur. Yani, aslında ?(x), fonksiyonun x=0'daki değerini, integralden "çekip" alır. Her ne kadar vektör fonksiyonu örneğimiz x=0 noktasında sonsuza gitse de, her durumda fonksiyonun sonsuza gittigi nokta x=0 olmak zorunda değil. Örneğin, x=a noktasında fonksiyon sonsuza gitsin. Ya da, keyfimiz gereği, fonksiyonun x=a noktasındaki değerini seçmek isteyelim. Öyleyse, x=a gibi bir noktada da Dirac delta fonksiyonunu tanımlamalıyız.

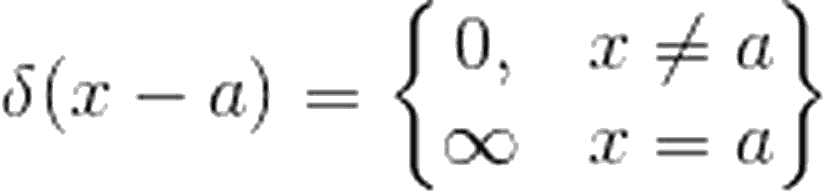
Kullandığımız mantık oldukça basit. ?(x), sadece içerisi 0 olduğunda 1 sonucunu vermekte. Öyleyse, içerisini x=a noktasında 0 yaparsak, x=a noktasında da Dirac delta fonksiyonunu kullanmış oluruz.

Benzer sekilde, x=a noktasında sıçrama yapan fonksiyonumuzun tüm uzaydaki integralinin sonucu 1'i verecektir.

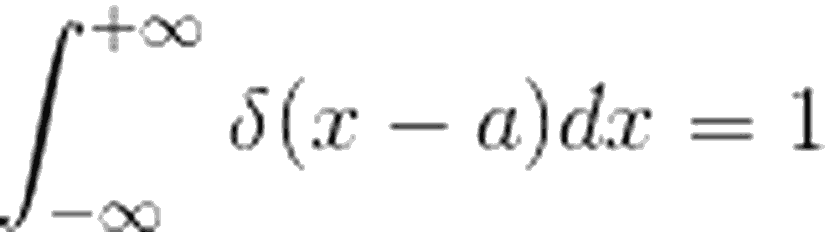
Dirac delta fonksiyonu, x=a noktasındaki değeri seçeceğinden:

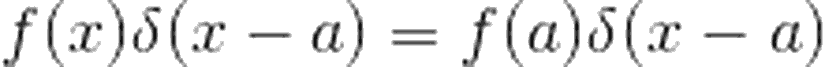
Haline gelir. Bu ifadenin integralini alırsak, yukarıdaki sonuca benzer olarak:

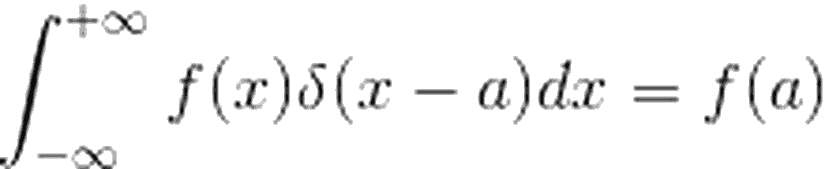
Elde etmiş oluruz. Bu sayede, herhangi bir a noktasında da Dirac delta fonksiyonunu kullanarak, integralden f(a)'yı seçmeyi başardık. Benzer şekilde, üç boyutta da dirac delta kullanılabilir.

Agora Bilim Pazarı

Çiftçi Ne Yapar?

Möööö… Gıt gıt gıdaaaak… Meeeeee…

Çiftçi sabah erkenden uyanıyor. Çünkü çok işi var:
Hayvanları besleyecek, inekleri sağacak, yumurtaları toplayacak, dev
traktörünün de yardımıyla tarlasına mısır, patates, buğday ekip biçecek… Biz
de sayesinde lezzetli sandviçler yiyip tazecik sütümüzü yudumlayacağız.
İŞTE SANA ÇİFTÇİ VE ÜRETTİĞİ LEZZETLİ GIDALAR HAKKINDA HARİKA
BİLGİLERLE DOLU BİR KİTAP.

Devamını Göster

₺110.00

Satın Al Tüm Ürünler

• Dış Sitelerde Paylaş

Dirac Delta Fonksiyonu ve Vektör Potansiyeli Örneği

İntegralimizin sonucunun 4π olduğunu söylemiştik. Öyleyse,

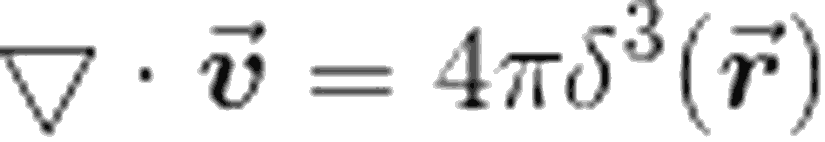
r vektörü 3 boyutta tanımlandığı icin için, 3 boyutta Dirac delta kullanmamız gerekiyor. 3 boyutta Dirac delta, "?³(r)" şeklinde ifade edilmekte. Yani ifade, fonksiyonun yalnizca (0,0,0) noktasındaki değerini 4π olarak vermekte. Geri kalan her yerde de 0 sonucunu vermekte.

Hazırlayan:Ege Can Karanfil
Editör: Ögetay Kayalı

Referanslar
1. David J. Griffiths, Introduction to Electrodynamics, 4th edition, Pearson
2. David J. Griffiths, Introduction to Quantum Mechanics, 2nd edition
3. Prof. Dr. Gürsevil TURAN, Quantum Physics ders notları
4. Wolfram, Delta Function, <https://mathworld.wolfram.com/DeltaFunction.html>
5. Science Direct, <https://www.sciencedirect.com/topics/engineering/dirac-delta-function>
Figürler
1. David J. Griffiths, Introduction to Electrodynamics, 4th edition, syf. 46
2. David J. Griffiths, Introduction to Electrodynamics, 4th edition, syf. 47