Skaler ve Vektörel Büyüklük Nedir? Boyut Analizi Nasıl Yapılır?
Birimler, Fizikte Başarıya Ulaşmak İçin Sandığınızdan Çok Daha Önemli!

- Özgün
- Fizik
Genel fiziğe girişte benimsenmesi gerek ilk üç kavram; boyut analizi, skaler ve vektör kavramıdır. Bu üçü genellikle çok ihmal edilen, fakat bir o kadar da önemli kavramlardır. Bugün olimpiyatlardan, en iyi üniversitelerin doktora alımlarında yapılan sınavlara kadar birçok yerde, sadece boyut analiziyle çözülebilen karmaşık sorular vardır. Bunun yanında skaler ve vektör kavramı, fiziğin mihenk taşlarıdır.
Fiziğin belki de en temel konusu, ilk öğrenilecek olan, onun matematikle arasına ince bir çizgi çekilmesini sağlayan birimlerdir. Bir odanın sıcaklığından bahsederken sadece 25 demeyiz, 25°C ifadesini kullanırız. Benzer şekilde bir arabanın hızı için 70 demeyiz (ve hatta "70 kilometreyle gidiyor" lafı da hatalıdır), 70 km/sa ifadesini kullanırız. Hatta daha da öteye gider, arabanın gittiği yönü de belirtiriz: "70 km/sa hızla güneye gidiyor." gibi... Bunlar fiziğe yeni başlayanlar için çok basit, sıradan veya önemsiz gibi görünebilir. Fakat üzerine düşülmediği takdirde, size her daim sorun çıkarabilecekleri gibi, önemsendiği takdirde işlerinizi çok kolaylaştırabilir!
Birimler
Mekanikte üç temel birim kullanılır. Bunlar; zaman (T\text{T}), uzunluk (L\text{L}) ve kütledir (M\text{M}). Bunlara ek olarak elektrik akımı (amper), sıcaklık (kelvin), mol ve kandela (cd) birimleri de bulunur. Diğer bütün fiziksel nicelikler (örn. hız, momentum, güç) çoğunlukla bu üç temel birim kullanılarak türetilir (bazı zamanlarda diğerlerine de ihtiyaç vardır). Zaman için genel olarak saniye (s), uzunluk için santimetre (cm) ve kütle için gram (g) kullanılır. Bunların ilk harflerinden türetilen bir şekilde bu sisteme cgs birim sistemi denir. Bir diğer birim sistemi ise SI birim sistemidir ve kilogram (kg), metre (m) ve saniye (s) birimlerini referans alır.
Elbette bu tek seçeneğimiz değil. Örneğin evren gibi büyük ölçeklerden bahsederken metreyi kullanmak yerine megaparsek (Mpc) ya da ışık yılı (ly) kullanmak çok daha akıllıcadır. Böylelikle çok büyük sayılardan kurtuluruz. Fakat bunlar arasında dönüşüm yaparken, yapılacak işlemlere dikkat etmek gerekir. Birçok öğrenci bu noktada hata yapıp, tuhaf sonuçlar bulur. Bu nedenle yaptığınız işlemlerin sonucunun akla yatkınlığını daima kontrol edin. Tam olarak bu noktada işinize yarayacak bir aracımız var, buna boyut analizi diyoruz.
Boyut Analizi (Birim Analizi)
Fizikte, yaptığımız cebirsel işlemlere birimler de dahil olur. Örneğin bir aracın hızı için, saatte 50 kilometre deriz. Bunun nedeni aşağıdaki denklemden anlaşılabilir.
X=V⋅t\Large X=V\cdot t
Hız (V\text{V}), uzunluğun (X\text{X} ya da biz boyut analizinde "uzunluk" (İng: "length") anlamında L\text{L} diyelim) zamana (t\text{t} ya da biz ona T\text{T} diyelim) bölümüdür. Dolayısıyla işlem yapılırken sadece sayılar değil, birimler de dahil olur. 50 km uzunluğunu 1 saate bölerseniz, 50 km/sa niceliğini elde edersiniz. Burada saatin başındaki değer 1 olduğundan ötürü başına 1 yazmayız, çünkü o birim zamanı ifade eder. Tüm bunlardan şu sonuç çıkarılabilir: Yapacağınız bazı işlemlerde pay ve paydada aynı anda yer alan birimler birbirini götürüp, sadeleşebilir.
Örneğin 50 km/sa değerini, m/s cinsinden bulmaya çalışalım. 1 km = 1000 m eder, 1 sa = 3600 s'dir. Eğer bunları denklemde yerine koyarsak:
V=Xt=50km1sa=50(1000m)1(3600s)=18.9m/s\Large V=\frac{X}{t}=\frac{50 km}{1 sa}=\frac{50(1000m)}{1(3600s)}=18.9m/s
olacağını görürüz. Biraz dikkatli bir göz, km/sa ifadesinden m/s ifadesine geçişin aslında 1/3.6 ile çarpmak olduğunu fark edecektir. Bu, kilometreden metreye, saatten ise saniyeye geçişin sonucunda gelen bir çarpandır.
Analiz Örnekleri
Konum hesaplarında sıklıkla kullandığımız bir denklemi ele alalım.
x=12at2\Large x=\frac{1}{2}at^2
Denklemin sol tarafında x\text{x}, yani uzunluk (L\text{L}) yer alıyor, dolayısıyla sağ tarafı da uzunluk biriminde olmalı. Fakat bu ilk bakışta o kadar belirgin görünmüyor. Denklemde ivme ve zamanın birimlerini yerlerine koyarsak:
x=12at2→L=LT2⋅T2\Large x=\frac{1}{2}at^2 \rightarrow L=\frac{L}{\cancel{T^2}}\cdot \cancel{T^2}
İvmeden gelen paydadaki saniye kare ifadesiyle, çarpım olarak gelen saniyenin karesi sadeleşir. Böylelikle geriye sadece uzunluk birimi kalır - ki bu da beklentilerimizi doğrular. Burada 1/2 çarpanının boyut analizinde bir etkisi olmadığı için göz ardı etmekte bir sakınca yok. O birimleri değil, sadece sonucun sayısal değerini etkiler.
Bir başka örneğe basit sarkacın periyodunu veren denklemden bakalım.
T=2πlg\Large T=2\pi \sqrt{\frac{l}{g}}
Soldaki T\text{T} ifadesi sarkacın periyodu, l\text{l} ifadesi sarkacın uzunluğu ve g\text{g} de çekim ivmesidir. Bu denklemdeki birimlerin tutarlı olduklarını görelim. İlk yapacağımız 2π2\pi ifadesini aradan çıkarmaktır. Bizi ilgilendiren katsayılar değil, birimler:
T=2πlg∼lg→LL/T2=(LL/T2)0.5=T\Large T=2\pi \sqrt{\frac{l}{g}} \sim \sqrt{\frac{l}{g}} \rightarrow \sqrt{\frac{L}{L/T^2}}=(\frac{\cancel{L}}{\cancel L/T^{\cancel 2}})^{\cancel {0.5}}=T
Böylelikle bu denklemi de boyut analiziyle kontrol etmiş oluruz.
Skaler Kavramı
Fiziğin ilk konularından biri olması sebebiyle çok göz ardı edilen bir konu olsa da, günümüzdeki en büyük teorik çalışmalarda bile adını duyabileceğiniz bir kavram skaler kavramıdır. Örneğin Büyük Patlama Teorisi'nin bazı problemlerine çözüm getiren Enflasyon Teorisi (İng: "Inflation Theory"), mekanizma olarak hipotetik bir "inflaton skaler alanı" ön görür. En basit haliyle skaler bir nicelik, sadece büyüklüğü olan, yönü olmayan bir niceliktir. Buna verilen en basit örnek genellikle sıcaklıktır. Bunun yanında kütle, hacim, sürat (hız değil!) ve elektrik yükü de skaler niceliklerdir.
Sezgisel olarak düşünmek adına, bunu bir noktadaki fiziksel gerçekliğin sayısal değeri olarak düşünebilirsiniz. Örneğin odanın içerisindeki spesifik bir noktanın, bir sıcaklık değeri bulunur. Fakat bundan başka bir şey (örneğin yön) belirtmez. Sadece nokta ve fiziksel anlam taşıyan değeri vardır.
Skaler kavramını biraz daha dallandıracak olursak, onların koordinat dönüşümleri altında değişmez olduklarını söyleyebiliriz. Başka bir deyişle Newton mekaniğinde dönme ve yansımalar altında, relativistik teorilerde ise Lorentz dönüşümleri altında değişmez olduklarını söyleyebiliriz.
Örnek Soru
Aşağıda verilen formül ideal gazların davranışı incelenirken kullanılır.
PV=nrT\Large PV=nrT
Burada; P\text{P} basınç (Pa), V\text{V} hacim (litre = dm³), n\text{n} mol, T\text{T} sıcaklık (Kelvin), R\text{R}'de gaz sabitidir. R\text{R}'nin değeri ve birimi, elimizde olan bilgilere göre değişmektedir. Bu soru için birimini (dm³·Pa)/(mol·K) olarak alalım.
Dikkat edildiğinde eşitliğin sol tarafında bulunan değerlerin boyutlarıyla, sağ tarafı birbirine denk olduğu görülebilir.
[Pa]⋅[L]3=[N]⋅[L]3⋅[Pa][N]⋅[K]⋅[K]\Large [Pa]\cdot [L]^3=[\cancel N]\cdot \frac{[L]^3 \cdot [Pa]}{[\cancel N] \cdot [\cancel K]} \cdot [\cancel K]
Yukarıdaki eşitlikte köşeli parantez içinde verilenler birimlerin boyutlarını göstermektedir. Burada [L]\text{[L]} uzunluğu ifade eder ve hacim üç uzunluğun (en, boy ve yükseklik) çarpımı olduğundan V\text{V} yerine L3L^3 kullanılmıştır.
(P+n2aV2)⋅(V−nb)=nRT\Large (P+\frac{n^2a}{V^2})\cdot (V-nb)=nRT
Formülün düzeltme yapılmamış hali için verilen incelemeden ve verilen birimlerden yararlanarak, ikinci formüldeki a\text{a} ve b\text{b} değerlerinin birimlerini bulmayı kendiniz de deneyebilirsiniz. Bulduğunuz sonucun doğruluğunu öğrenmek isterseniz, aşağıdaki çözümü okuyabilirsiniz.
Çözüm
Bu sorunun çözümü için öncelikle bilinmesi gereken, iki büyüklüğün toplanabilmesi ya da birbirinden çıkarılabilmesi için birimlerinin aynı olması gerektiğidir. Aynı birimli iki büyüklükle toplama ya da çıkarma işlemi yapıldığında sonuç da bu birime sahip olacaktır. Hiç kuşkusuz 5 elma ile 3 kalemi toplayıp, buna 8 elma diyemeyiz. Örneğin 1 m + 100 K işlemi anlamsızken, 1 m + 1 m = 2 m olur.
İkinci olarak bilinmesi gereken ise birimlerle çarpma ve bölme işlemidir. Bu işlemler yapılırken birimlere de tıpkı sayılar gibi davranılır. Pay ve paydada ortak bulunan birimler sadeleştirilir, aynı birim kendisiyle çarpıldığında üssü buna göre değişir ve farklı birimler aynı işlemde kullanılabilir (toplama ve çıkarmanın aksine).
2. denklemin ilk teriminde basınç artı bir ifade bulunmaktadır. Toplanabilmeleri için bu ifadenin de basınç cinsinden olması gerektiğini biliyoruz. Dolayısıyla V2⋅Pa/n2V^2\cdot Pa/n^2 ifadesini a \text{a }ifadesi yerine koyarsak Pa\text{Pa} cinsinden bir değer kalır. Soruda V\text{V}'nin birimi dm3 olarak verildiğinden bu ifadeyi yerine koyarsak a\text{a} ifadesi için dm6.Pa/n2olduğunu görürüz.
İkinci parantezin içinin ise hacim olması gerektiği anlaşılıyor (hacimden hacim çıkarılabilir). Bu durumda çıkarma işleminin yapılabilmesi için ikinci terim olan nb\text{nb}'nin de birimi hacim olmalı. Boyut analizinden yararlanacak olursak hacmin boyutunun [L]3[L]^3 olduğunu ve mol sayısı anlamına gelen n\text{n}'nin [N]\text{[N]} şeklinde gösterildiğini biliyoruz. Öyleyse:
n⋅b=[N][L]3[N]→b=[L]3[N]\Large n\cdot b=[\cancel N]\frac{[L]^3}{[\cancel N]} \rightarrow b = \frac{[L]^3}{[N]}
olur. Boyutuyla değil soruda istendiği şekilde birimiyle yazarsak da b\text{b}'nin birimi dm3/n olacaktır.
Vektör Kavramı
Vektör, büyüklüğü (ya da uzunluğu) ve yönü olan geometrik bir niceliktir. Kimi zaman geometrik vektör, uzaysal vektör veya Öklidyen vektör de denilir. En basit tabiriyle, yön kavramı eklenmiş skaler nicelik gibi düşünebilirsiniz. Örneğin hız bir vektöreli niceliktir. Hızı ifade edebilmek için, sadece sayısal bir değer yetmez. Çünkü hız, hareketin varlığını içerir, dolayısıyla bir yönü vardır. Mesela bir araç 50 km/sa hızla kuzey yönünde ilerlemektedir dediğimiz zaman bir hız ifadesinden bahsederiz.

Sıklıkla karıştırılan bir kavram da sürattir. Sürat ise daha ziyade gündelik hayatta kullandığımız, hızın sadece büyüklüğünü ifade etmek için kullandığımız skaler bir kavramdır. "Araç 50 km/sa sürate sahiptir." deriz (her ne kadar gündelik dilde "hız" desek de fizik için bunun doğrusu "sürat"tir). Dolayısıyla sadece sayısal bir değeri olduğundan sürat bir skalerdir, fakat ona yön ekleyip, aracın kuzeye gittiğini söylersek işte o zaman hızdan bahsetmiş oluruz.
Vektörel niceliklere bazı örnekler olarak; hız, yer değiştirme, çizgisel momentum, açısal momentum, kuvvet ve ivme gösterilebilir.
Vektörlerle de aynı zamanda bir takım işlemler yapabiliriz, örneğin toplamak ve çarpmak gibi. Fakat özellikle çarpım (biz buna farkı belirtmek için vektörel çarpım deriz), alışık olduğumuz skaler çarpıma göre farklıdır. Vektörlerle ilgili olan bu tür matematiği, vektör cebiri altında inceleriz.
Tüm bunlar bir fizikçinin, olmazsa olmaz araçlarıdır. Eğer bir alet çantamız olsaydı, içerisinden bunları asla eksik etmezdik.
Örnek Soru
Vektörler ve skalerlerle ilgili aşağıdaki yargıların doğruluğuna karar vermeye çalışın.
- Referans sistemi belli bir noktaya göre hareketi incelememizi sağlayan koordinat sistemidir. Hız bu koordinat sistemi kullanılarak incelenir ve belirlenir. Sürat, hızın aksine skaler yani yönsüz bir büyüklük olduğundan belirlenmesi için bir referansa ihtiyaç yoktur.
- Bir cismin belli bir andaki hızının büyüklüğü ve sürati birbirinden farklı olabilir.
- Vektörler yönlü büyüklükler olduklarından negatif değerler alabilirler. Bunların negatif olması, pozitif seçilen yönün aksine hareket ettikleri anlamına gelir. Ancak skaler büyüklükler yön belirtmediklerinden negatif değer alamazlar.
- Ağırlık, kütle çekiminin bir cisme uyguladığı kuvvetin ölçüsü olarak tanımlanır. Kuvvet, vektörel bir büyüklük olduğundan ağırlık da (kütlenin aksine) vektöreldir.
Cevaplar
Cevap-1: Süratin skaler, hızın ise vektörel büyüklükler olduğu doğrudur. Ancak her ne kadar sürat yönsüz bir büyüklük olsa da büyüklüğü bizim seçtiğimiz referansa göre değişiklik gösterir. Yani herhangi bir referans noktası belirlemeden süratten bahsetmek imkânsızdır.
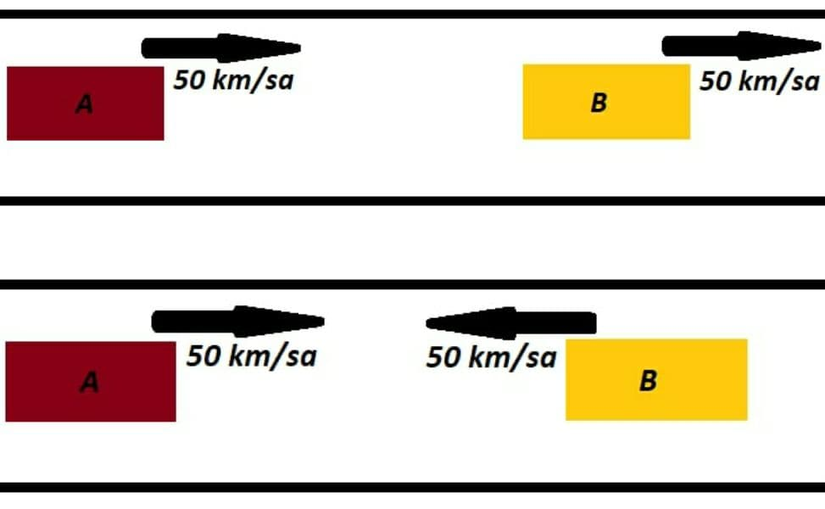
Cevap-2: Örneğin sabit kabul ettiğimiz yola göre saatte 50 km süratle hareket ediyor olun. Bu durumda süratiniz yere göre 50 km/sa olacaktır. Önünüz de iki tane daha araç olduğunu, bunlardan birinin saatte 50 km süratle size doğru geldiğini öbürünün ise saatte 50 km hızla sizinle aynı yönde gittiğini hayal edin. Bu durumda sizin sizinle aynı yönde giden araca göre süratiniz 0 km/sa olurken, size doğru gelen araca göre süratiniz 100 km/sa olacaktır.
Sürat, tanım olarak hızın büyüklüğüdür. Çembersel bir hareketi ele alacak olursak, hızın değiştiğini ama süratin sabit kaldığını görürüz. Burada hızın değişmesinin nedeni, vektörün yönünün değişmesidir. Eğer büyüklüğü olan sürat de değişecek olursa hareket çembersel değil, gezegenlerdeki gibi eliptik olacaktır (bkz. Kepler yasaları).
Cevap-3: Genelde hepimizin alışık olduğu ve sorularda sıkça karşılaştığı referans sistemi, sağ ve yukarı yönü pozitif, sol ve aşağı yönü negatif kabul eder. Ancak bu yalnızca bir kabuldür ve karşılaştığınız problemlere göre bunu değiştirebilirsiniz. Önemli olan yönleri bir kez belirledikten sonra problemin sonuna kadar buna sadık kalmanızdır. Verilen üçüncü ifadeye dönecek olursak bu ifadenin ilk kısmı doğrudur. Problemi çözerken seçtiğiniz yöne göre negatif değerli vektörel bir büyüklük, seçtiğiniz negatif yönü gösteriyor demektir. Ancak bu, skaler büyüklükler negatif olamaz demek değildir. Örneğin sıcaklık sıfırın altında olabilir, bunda herhangi bir sakınca yoktur. Fakat vektörlerden farklı olarak skaler bir büyüklüğün negatif olması onun yönü hakkında hiçbir bilgi vermez.
Cevap-4: Ağırlık bir kuvvettir ve doğal olarak vektöreldir.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 42
- 28
- 18
- 13
- 6
- 5
- 2
- 2
- 2
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 20/04/2024 09:39:25 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12905
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.






