Atom Modelleri: Bohr Atom Modeli
- Özgün
Nükleer teknolojilerin gelişmesiyle birlikte, atomun yapısı daha iyi anlaşılmaya başladı. 1908 yılında Rutherford liderliğinde yürütülen çalışmalarda, atom çekirdeğinin, atomun çok küçük bir hacmini oluşturduğu keşfedildi. Bu keşfin hemen ardından, Rutherford yeni bir atom modeli öne sürdü ve gözlemleri açıklamaya çalıştı. Fakat bu model, klasik elektrodinamikle ciddi çelişkiler içeriyordu.
Bohr Atom Modeli
Rutherford atom modelindeki çelişkileri gidermek için, 1913 yılında Niels Bohr tarafından yeni bir atom modeli geliştirildi. Bohr atom modeli olarak anılan bu model, Rutherford'un elektronu Güneş etrafında dönen gezegenlere benzettiği modelinden, Max Planck'ın kuantum hipotezinden ve Einstein'ın foton konseptinden faydalanarak geliştirilmişti.
Üç önemli önerme içeren Bohr atom modeli, başta hidrojen olmak üzere, tek elektronlu element atomlarının enerji seviyelerini oldukça başarılı şekilde açıklıyordu. Bu önermelere geçmeden önce, Rutherford atom modelinin sahip olduğu sorunları incelemek faydalıdır. Çünkü Bohr atom modeli, buradaki sorunlara bazı açıklamalar getirmiş olsa da günümüzdeki atom modeli değildir ve bunların ayrımlarını iyi anlamak gerekir.
Rutherford Atom Modelinin Sorunları
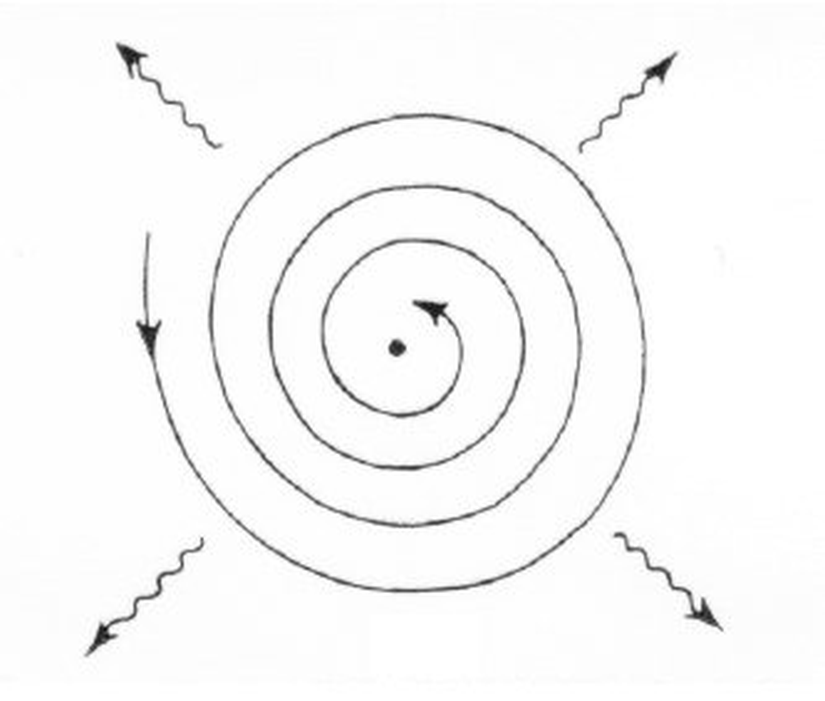
Rutherford tarafından geliştirilen atom modeli, bu gözlemler ışığında, çekirdeğin etrafında çembersel ya da eliptik yörüngede dönen elektronlar olduğunu söylüyordu. Lakin bu model, klasik elektrodinamik ile çelişkiler içermekteydi. Klasik elektrodinamiğe göre, ivmelenen bir yüklü parçacık, elektromanyetik dalga yaymalıydı. Bu da demek oluyor ki, atom çekirdeğinin etrafında dönen elektron, enerji kaybetmeliydi. Bu enerji kaybı, elektronun spiral çizerek 10⁻¹⁰ saniye kadar kısa bir sürede çekirdeğe düşmesine sebep olacaktı.
Atom modelinin diğer bir önemli sorunu da yine klasik elektrodinamikten geliyordu. Klasik elektrodinamiğe göre, ivmelenen yüklü parçacığın oluşturduğu elektromanyetik dalganın frekansı, parçacığın hareketinin periyoduyla doğru orantılı olmalıydı. Rutherford atom modelindeki elektronun periyodu, o zamanlar bilinen atom spektrumlarıyla kesinlikle uyuşmuyordu.
Tüm bunlar ışığında, 1913 yılında Niels Bohr tarafından, 3 önermeye sahip yeni bir atom modeli öne sürüldü. Ayrıca bakınız:
Thomson Atom Modeli ve Rutherford Atom Modeli
Kuantum Mekaniği: de Broglie Dalga Boyu
Bohr Atom Modeli Özellikleri
Bohr atom modeline göre:
- Atom, yalnızca belirli enerji seviyelerine sahip olabilir. Bu enerji seviyelerindeki elektronlar, kararlı yapıdadır ve elektromanyetik ışıma yapmazlar.
- de Broglie hipotezine göre, bu kararlı yörüngelerdeki elektronlar, dalga gibi hareket ederler. Elektronun yörüngesindeki dalgaboyu sayısının tam sayı olması gerektiğinden, bir enerji seviyesindeki elektron için aşağıdaki ifadeyi yazabiliriz:
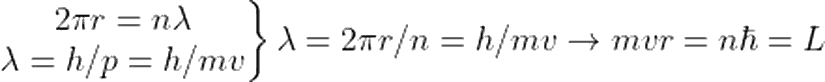
- Elektron, yüksek enerjili bir yörüngeden daha az enerjili bir yörüngeye inerken ışıma yapar. Bu değişimde yayınlanan fotonun frekansı, iki yörünge arasındaki enerji farkına bağlıdır. Yayınlanan fotonun frekansı için aşağıdaki enerji korunum bağıntısı kullanılır.
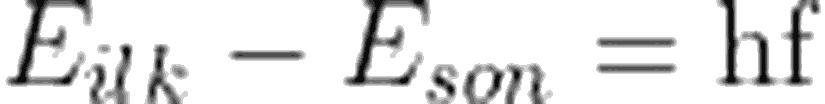
Benzer bir durum, soğrulan elektromanyetik dalgalar için de geçerlidir. Yani yeterli bir enerjiye sahip fotonun soğurulması durumunda, elektron bir üst yörüngeye geçiş yapabilir.
Bohr Atom Modeli İçin Enerji İfadesinin Türetilmesi
Bohr atom modelinin yukarıdaki üç önermesini kullanarak, tek elektronlu atomlar için enerji ifadesini elde etmek son derece kolaydır. Dairesel yörüngede dönmekte olan elektrona yaptığı dairesel hareketten dolayı merkezcil kuvvet etki eder. Zıt cins elektrik yüküne sahip çekirdek ve yörüngesinde dolanan elektron birbirine Coulomb kuvveti uygular. Dairesel yörüngede hareket eden cisimlere etki eden bileşke kuvvet, merkezcil kuvvettir. Dolayısıyla elektrona etki eden Coulomb kuvveti, merkezcil kuvvetle aynı şiddette olur. Yani, atom numarası Z olan, tek elektronlu bir element atomu için aşağıdaki eşitliği yazabiliriz:
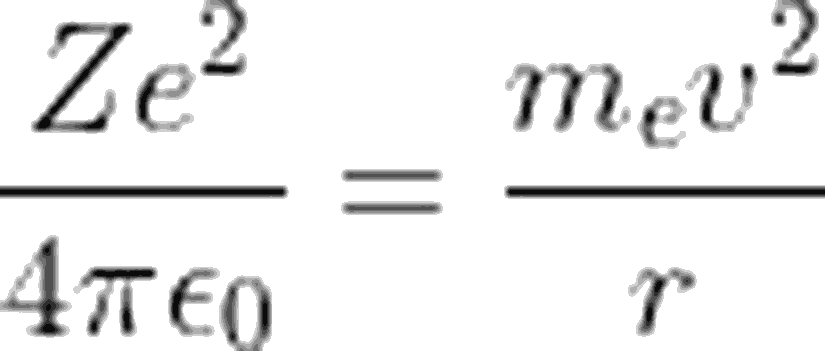
Bu eşitlikten hız ifadesini çekip, açısal momentumun kuantizasyonu ifadesiyle birlikte düzenlersek
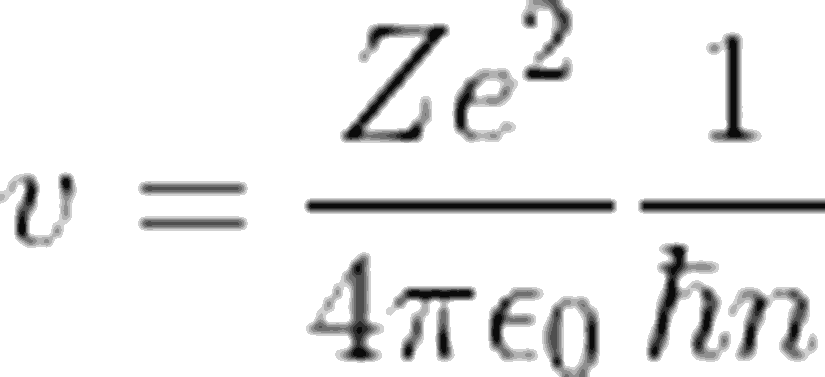
ifadesini elde ederiz. Benzer şekilde, yarıçap (r) için de yukarıdaki işlemi gerçekleştirir ve hız ifadesini de yerine yazarsak, aşağıdaki ifadeyi elde etmiş oluruz:
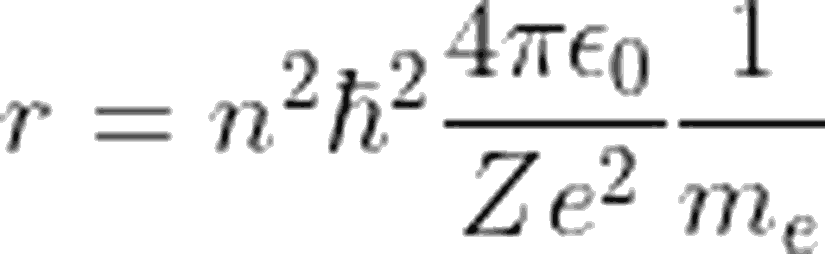
Artık sistemin toplam enerjisini yazmaya hazırız. Biliyoruz ki toplam enerji, kinetik ve potansiyel enerjinin toplamı anlamına gelir. Bohr atom modelinde, hareket eden parçacık elektron olduğu için, kinetik enerji ifadesinde yalnızca elektron yer alır. Potansiyel enerji de yalnızca çekirdekteki pozitif yükler ile elektron arasında oluşacağından, toplam enerji ifadesini aşağıdaki gibi yazabiliriz:
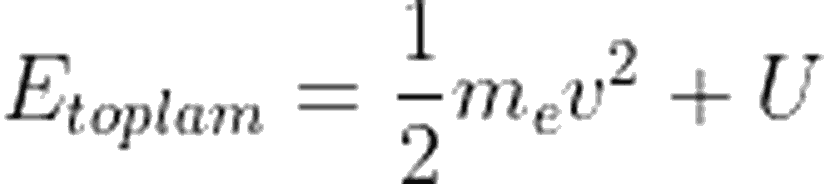
Elektrik potansiyel enerjisini
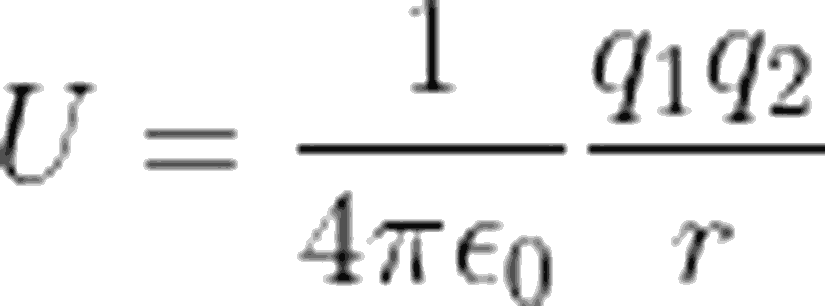
şeklinde ifade edebiliriz. Elektrik potansiyel enerjisini toplam enerji ifadesinde yerine yazalım:
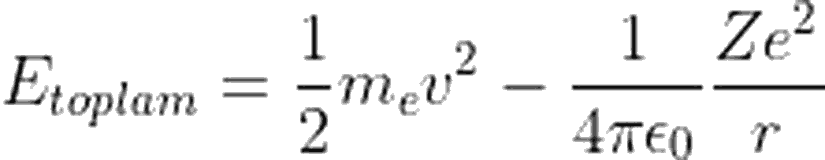
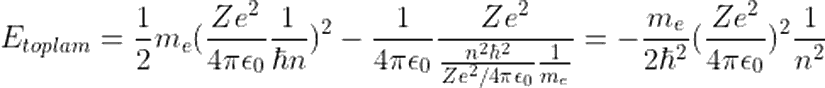
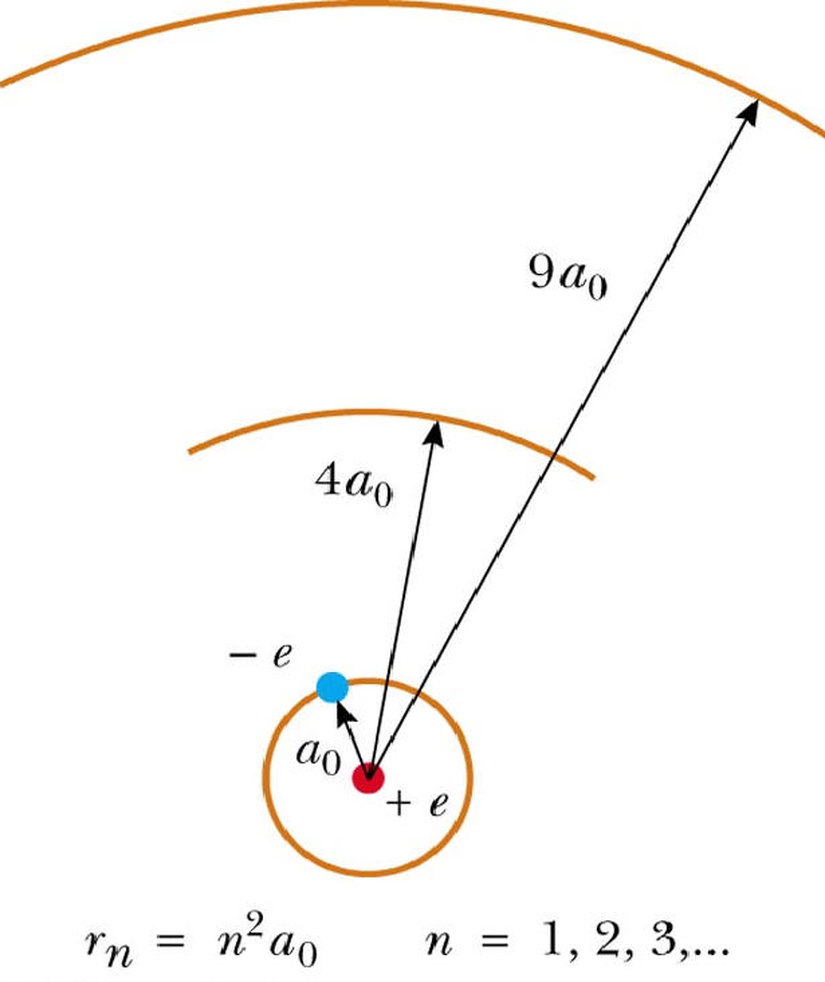
Hidrojen Atomu İçin Bohr Atom Modelinin Çözümü
Hidrojen atomu için (Z=1) yukarıdaki ifadeyi çözecek olursak:
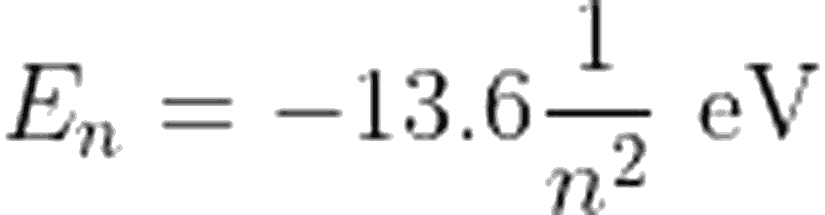
ifadesini elde ederiz. Öyleyse n=1 durumunda (taban durumu), Hidrojen atomundaki elektronun enerjisi -13.6 eV'dir. Benzer şekilde, yarıçap ifadesini de hidrojen atomu için düzenlersek,
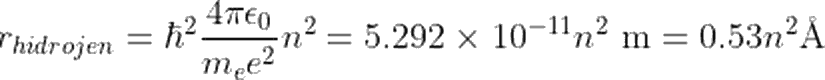
halini alır. Benzer şekilde, n=1 durumu için, yarıçap değerinin 0.53 Å olduğunu görebiliriz. Bohr yarıçapı adı verilen bu yörünge, hidrojen atomunun en küçük yarıçaplı yörüngesidir.
Tek Elektronlu Elementler
Yukarıdaki işlemlerimizi, atom numası Z olan tek atomlu elementler için yapmıştık. İfadelerimizi, Hidrojen atomu için yaptığımız hesapları kullanarak genelleyecek olursak:
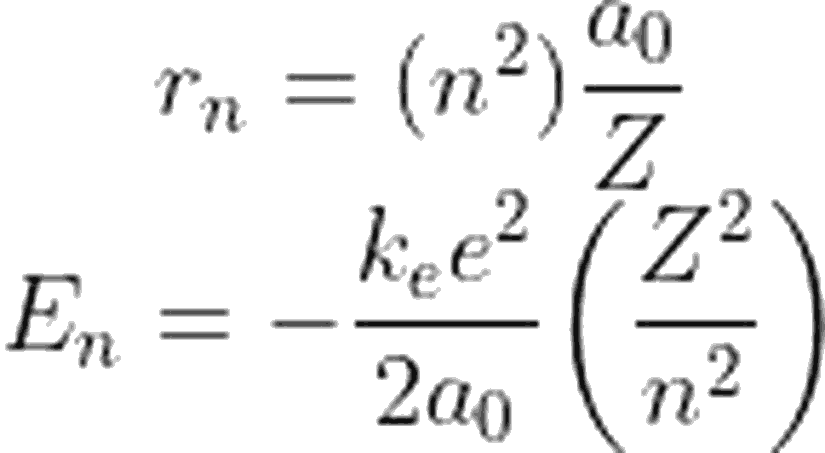
Burada a₀, 0.53Å, kₑ ise1/4πε₀anlamına gelmektedir.
Bilim tarihinde, kuantum fiziğine giden yoldaki önemli köşe taşlarından birisi olan Bohr atom modeli, Max Planck'ın ortaya attığı kuantum görüşünü kullanarak, atomaltı dünyayı anlama yolunda büyük bir adımdır.
Bohr Atom Modelinin Açıklayamadığı Olaylar
Bohr atom modelinin açıklayamadığı (bir başka deyişle eksik kaldığı) noktalar:
- Bohr Atom Modeli tek elektronlu atomları açıklamakta yeterli iken birden fazla elektronu olan elementleri açıklayamamaktadır. Bunun başlıca sebeplerinden biri; çok elektronlu elementlerde çekirdeğin etrafındaki yörüngelerde bulunan elektronların birbirlerini perdelemesinden (girginlik) ötürü, seviyelerin enerji değerleri ölçümleri gerçek değerlerinden saparak hatalı sonuç vermiştir.
- Bohr Atom Modelinde elektronun konumu ve momentumu ile ilgili kesinlik mevcuttur. Herhangi bir yörüngedeki elektronun konumu ve hızını aynı anda aynı duyarlılıkla ölçülebildiği hesaplanmıştır. Halbuki Heinsenberg belirsizlik ilkesine göre bir elektronun konumu ve momentumu aynı duyarlılıkla ölçülemez. Bohr atom modeline göre elektronun bulunacağı yer bellidir, aynı zamanda bulunduğu yörünge yarıçapı keskinlikle hesaplanır. Lakin Modern atom Teorisinde elektronun bulunma olasılığının yüksek olduğu bölgeler vardır (bu bölgelere orbital adı verilir) ve elektronun yeri kesin olarak belirlenemez.
- Modern atom teorisine göre elektron dalga özelliğine sahip olduğu için , Bohr atom modelinin savunduğunun aksine hareketi dairesel değildir.
- Bohr atom modelinde elektronun dalga-parçacık ikililiği göz önüne alınmamıştır.
- Çok elektronlu sistemlerin spektrumlarını açıklamakta yetersiz kalır. Çok elektronlu atomların spektrumlarında enerji düzeylerinin her birinin iki ya da daha fazla düzeye ayrıldığı görülmektedir.
- Bazı spektrum çizgilerinin dış manyetik alan etkisiyle daha alt çizgilere ayrılmasının sebepleri açıklanamamıştır.
- Atom spektrumu incelendiğinde bazı çizgilerin diğerlerinden daha parlak oluşunun sebepleri açıklanamamıştır.
- Atomlar arası bağlar ve molekül oluşumu açıklanamamıştır.
- Bohr Atom Modelinde nötron yoktur. Nötronlar, 1932 yılında James Chadwick tarafından keşfedilmiştir.
Bütün bu maddeler Bohr atom modelinin eksileridir, lakin o dönemde Rutherford atom modelinin üzerine getirdiği artılar sayesinde, bilim birbiri üzerine inşa ederek, birbirini yanlışlayarak, günümüzdeki noktaya gelebilmiştir ve ilerlemeye devam etmektedir.
Hazırlayan: Ege Can Karanfil & Büke Özen
Referanslar
1. Stephen Gasiorowicz, Quantum Physics, 3rd Edition
2. Prof. Dr. Osman Yılmaz, Quantum Physics ders notları
3. David J. Griffiths, Introduction to Quantum Mechanics, 2nd edition
4. Prof. Dr. Gürsevil TURAN, Quantum Physics ders notları
5. Serway ve Beichner, Fizik 3 (Modern Fizik) 5. Baskı, Syf. 1305
6. Nobel Prize 1922, http://www.nobelprize.org/nobel_prizes/physics/laureates/1922/
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 19/04/2024 13:59:42 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12751
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.




