Ağ Modelleri Nelerdir? Ağ Biliminde Nasıl Kullanılırlar?
 Silicon Republic
Silicon Republic
- Özgün
- Grafik Teorisi
Ağ bilimi literatüründe birçok farklı ağ topolojisi bulunur. Ancak bu yaklaşımlar temelde birkaç temel ağ modellerine dayanmaktadır. Ağ modellerini oluşturan temel topolojiler yüzük örgü (İng: "ring lattice"), küçük dünya (İng: "small world"), Erdös rassal, çekirdek çevresi (İng: "core periphery"), ölçekten bağımsız (İng: "scale-free") ve gözeli (İng:"cellular") şeklindedir. Bu temel topolojiler aşağıda gösterilmiştir:
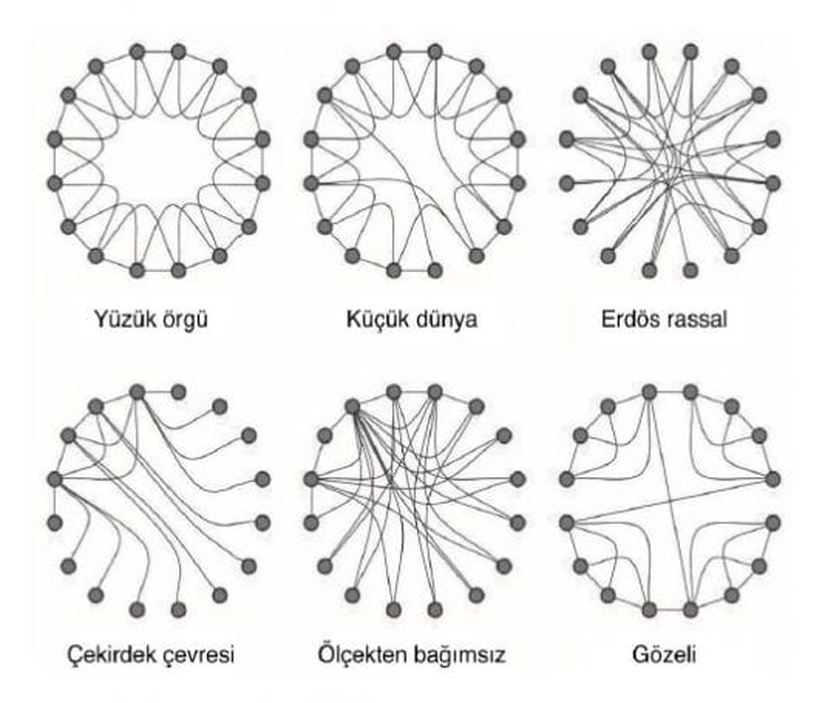
Yüzük örgü topolojisinde her düğüm, kendi komşusuna bağlıdır. Küçük dünya topolojisinde ise her düğüm birçok komşu düğümüne ve birkaç uzak düğüme bağlıdır. Erdös rassal topolojide her düğüm diğer düğümlere rastgele şekilde bağlıdır. Çekirdek çevresi topolojide düğümler yalnızca merkezi düğümlere, merkezi düğümler de birbirine bağlıdır. Ölçekten bağımsız topolojide birkaç merkezi düğüm diğer düğümlere bağlıdır. Gözeli topolojide ise ağ komünitelere ayrılmıştır; diğer bir deyişle düğüm grupları vardır ve her grup kendi içerisinde sıkı, diğer gruplarla seyrek bağlanmıştır.
Ağ biliminin tarihsel gelişimi göz önünde bulundurulduğunda üç adet teorik modelin temel modeller olduğu ve literatürdeki makale ve kitaplarda ağırlıklı olarak geçtiği görülmektedir. Bunlar Rassal ağlar (Erdös rassal), ölçekten bağımsız ağlar ve küçük dünya ağlarıdır.
Ağ Modelleri
Rassal Ağ Modeli
Rassal ağlar (İng: "random networks"); düğüm sayısının belli, diğer tüm parametrelerin rastgele olduğu ağlardır. Diğer bir deyişle NN adet düğümün arasındaki EE adet bağlantı rastgele yerleşmiştir. Yani her iki düğüm arasında belli bir pp bağlanma olasılığı vardır ve E E sayısı da buna göre belirlenir.
Bağlanma olasılığından ötürü rassal ağlarda hiçbir düğüm arasında bağlantı olmayabilir veya her düğüm arasında bağlantı da olabilir. Bu nedenle daha doğru bir tanımlama yapılırsa, tek bir ağ üzerinden rastgeleliğin konuşulması doğru değildir. Bunun yerine G(N,p)G(N,p) şeklinde bir ağlar kümesinin tanımlanması ve içindeki her elemanın (her bir GG ağı)
P(G)=pE(1−p)(N2)−EP(G) = p^{E}(1-p)^{\binom{N}{2}-E}
olasılığına göre elde edilmesi gereklidir. Görüldüğü üzere rassal ağlarda sadece iki düğüm arasındaki bağlantı olasılığı sabitlenir. Bağlantı sayısı da başlangıçta sabit olmamakla birlikte beklenen değeri hesaplanabilir. EE adet bağlantıya sahip bir ağın kümeden seçilme olasılığı
P(E)=((N2)E)pE(1−p)(N2)−EP(E) =\dbinom{\binom{N}{2}}{E} p^{E}(1-p)^{\binom{N}{2}-E}
şeklindedir ki bu da Binom dağılımıdır. Ancak ağın büyüklüğü yani düğüm sayısı çok arttığı zaman derece dağılımı Poisson dağılımını verir. Bir rassal ağda EE sayısı belli ise ortalama derece ve kümelenme katsayısı için sırasıyla şunlar yazılabilir:
<k>=2EN , C=<k>N−1<k>= \frac{2E}{N}\space, \space C=\frac{<k>}{N-1}
Bu ağ topolojisine Erdös-Renyi modeli de denmektedir.
Küçük Dünya Ağ Modeli
Bu modelde, bir ağdaki düğümler komşu olmadıkları düğümlere bile az sayıda adımda ulaşabilmektedir. Ortalama yol uzunluğunun küçük, kümelenme katsayısının büyük olduğu ağlardır. Watts-Strogatz modeli olarak da bilinen küçük dünya ağları düzenli bir ağ (örneğin yüzük örgü topolojisi) ile rassal ağ arasında kalan bir yapıya sahiptir. Watts tarafından 2003 yılında tanımlanan ve 0 ile 1 arasında değerler alabilen ββ parametresi sıfır durumunda düzenli, bir durumunda rassal ağ oluşturur. Küçük dünya ağları bu ββ aralığının ortalarında yer almaktadır.
ββ parametresinin sıfır ve bir değerlerine göre ortalama yol uzunluğu l(β)l(β) ve kümelenme katsayısı C(β)C(β) aşağıdaki gibidir:
}\space,\space l(1) = \frac{\ln N}{\ln()} \\
C(0)=\frac{3}{4}\space,\space C(1) =\frac{}{4}">l(0)=N2<k> , l(1)=lnNln(<k>)C(0)=34 , C(1)=<k>4l(0) = \frac{N}{2<k>}\space,\space l(1) = \frac{\ln N}{\ln(<k>)} \\
C(0)=\frac{3}{4}\space,\space C(1) =\frac{<k>}{4}
Derece dağılımı da ββ'ya ve kümelenme katsayısına bağlı olarak da formülize edilebilir ve β=1β=1 durumunda Poisson dağılımını verir.
Ölçekten Bağımsız Ağ Modeli
Doğal ve yapay tüm sistemlere rassal ve küçük dünya ağ modellerinden daha fazla uyan, ölçekten bağımsız ağ modeli adı altında bir model vardır. Derece dağılımları kuvvet yasası formundadır. Şöyle ki, bir düğümün k adet bağlantısı olma olasılığı şöyle belirlenir:
P(k)∼k−γP(k) \sim k^{-\gamma}
Burada γ\gamma derece üstelidir. Bu tip ağlarda bir düğümün çok fazla bağlantısının olma olasılığı rassal ağlardan daha yüksektir. Bu da merkez düğümlerin ağın özelliklerinden biri olduğunu göstermektedir.
Ağın büyümeye müsait ve öncelikli bağlantı (İng: "preferential attachment") içeren yapıları ölçekten bağımsız ağları oluşturan iki temel bileşendir. Büyüme, ağdaki düğüm sayısının zamanla artması demektir. Öncelikli bağlantı ise ağa eklenecek yeni bağlantıların, bağlantı sayısı fazla olan düğümler ile olmasının daha yüksek olasılıkta olduğuna işaret etmektedir. Matematiksel olarak bağlanma olasılığı şu şekildedir:
P(ki)=ki∑i=1NkiP(k_i) = \frac{k_i}{\sum\limits_{i=1}^Nk_i}
Bu model Barabasi ve Albert tarafından 1998 yılında geliştirilmiştir. Modeldeki ortalama yol uzunluğu olan
<l>=lnNln(lnN)<l> = \frac{\ln N} {\ln(\ln N)}
paydadaki çift logaritmik düzeltme ile hesaplanabilir ve düğüm sayısı ile logaritmik şekilde artmaktadır. Bu modelin ortalama yol uzunluğu rassal ağlara göre küçüktür. Ölçekten bağımsız ağ heterojen, rassal ağlar homojen topolojide sayılabileceğinden ötürü ölçekten bağımsız ağ yapısı düğümleri birbirine daha fazla yaklaştırmaktadır. Kümelenme katsayısı da rassal ağlara göre daha büyüktür. Bu katsayı bir kuvvet yasası izleyerek, düğüm sayısının artmasıyla azalmaktadır.
Ölçekten bağımsız ağların derece dağılımı hiyerarşik şekilde olduğu için rastgele bir düğümü hedef alan ataklara karşı rassal ağlardan daha savunmasızdır. Merkez düğüm devreden çıktığı zaman ağın bütünlüğü bozulacaktır. Rassal ağlarda ise bağlantılar genellikle homojen bir dağılım gösterdiği için düğüm eksilmelerine daha dayanıklıdır. Diğer düğümler aralarındaki bağlantıları koruyabilir.
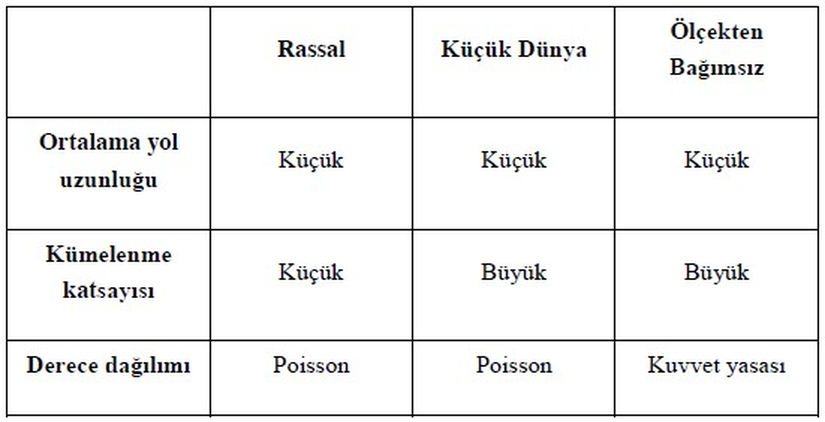
Buraya kadar değinilen üç temel ağ modeli ile ilgili derece dağılımı, kümelenme katsayısı ve ortalama yol uzunluğunun özeti aşağıdaki çizelgede verilmiştir.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 2
- 1
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- S. Tüzüntürk. (2012). Ağ Bilimi. ISBN: 9786054485697. Yayınevi: Dora Yayınları.
- M. Newman. (2010). Networks. ISBN: 9780191500701. Yayınevi: OUP Oxford.
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 26/04/2024 02:01:34 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12951
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.




