Ağ Bilimi Nedir? Bir "Ağ" Nasıl Tanımlanır? Ağ Türleri Nelerdir?
 iStockphoto
iStockphoto
- Özgün
- Grafik Teorisi
Bir ağ (İng: "Network"), en basit tanımıyla çizgilerle birbirlerine bağlanmış noktaları ifade eder. Matematiksel olarak ağlar "çizge", noktalar "köşe" ve çizgiler "kenar" olarak adlandırılır. Bu niceliklerin bilgisayar bilimlerindeki karşılığı ise "ağ", "düğüm" ve "bağlantı" kavramlarıdır. Fiziksel, biyolojik ve sosyal bilimlerdeki birçok sistem ağlar şeklinde ifade edilebilir. Düğüm ve bağlantıların çeşitli sistemlerdeki karşılıkları aşağıda gösterilmiştir.
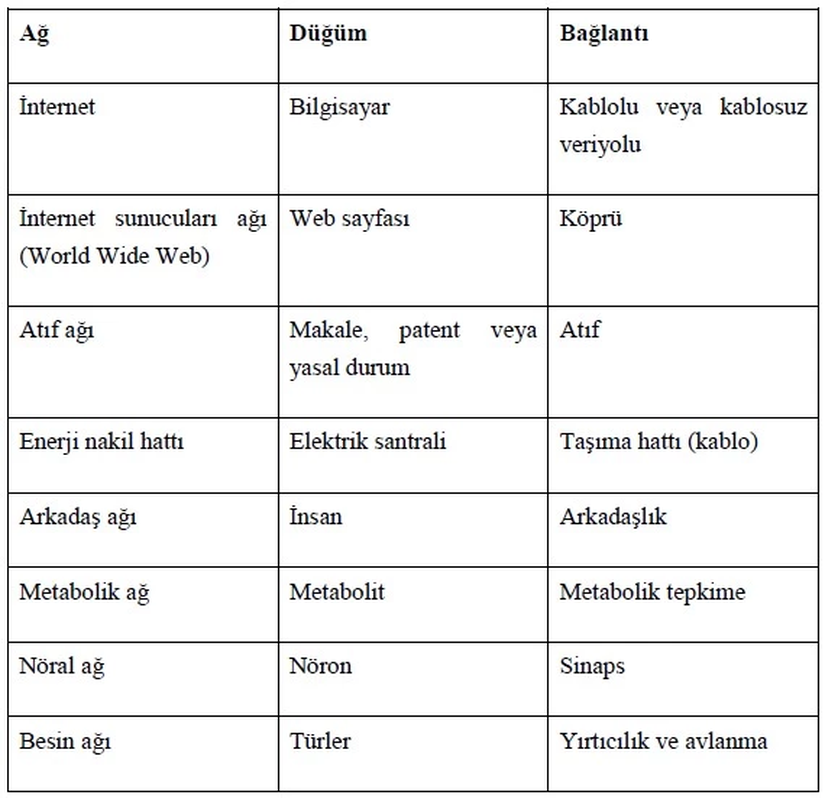
Çoğu ağda iki düğüm arasında tek bağlantı bulunur. Bazı durumlarda çoklu bağlantılar da görülebilmektedir. Bununla birlikte bazı düğümler kendilerine de bağlantı yapabilirler.
Bağlantılarına Göre Ağ Türleri
Ağ biliminde, bir ağda çoklu bağlantı veya kendine bağlantı yoksa bu ağ basit ağ olarak adlandırılır. Eğer çoklu bağlantı varsa ağa çoklu bağlantılı ağ, eğer kendine bağlantı varsa ağa kendine bağlantılı ağ adı verilir.
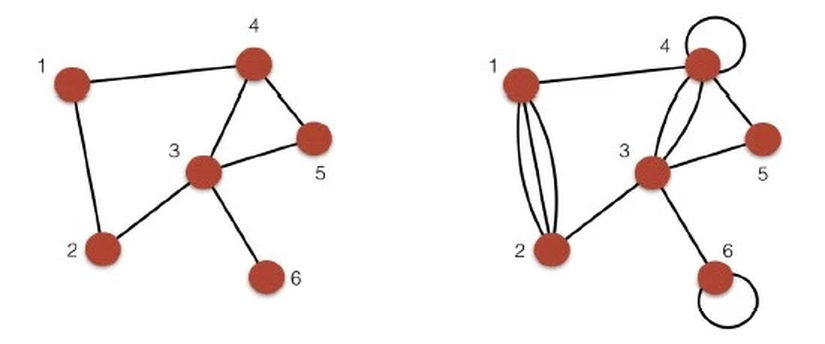
Ağ biliminde ağların matematiksel olarak ifade edilebilmeleri için farklı yollar vardır. Bir ağın bitişiklik matrisi olan AA, kare bir matristir ve her bir eleman AijA_{ij} olacak şekilde şöyle yazılabilir:
Aij={1,i ve j bag˘lı0,i ve j bag˘lı deg˘ilA_{ij}=
\begin{cases}
1,& \text{i ve j bağlı}\\
0, & \text{i ve j bağlı değil}
\end{cases}
Çoklu bağlantılar veya kendine bağlantılar da bitişiklik matrisinde yer alabilir. Yukarıdaki ağların bitişiklik matrisi aşağıdaki gibidir:
(010100101000010111101010001100001000),(030100301000010211102210001100001002)\begin{pmatrix}
0&1&0&1&0&0 \\
1&0&1&0&0&0 \\
0&1&0&1&1&1 \\
1&0&1&0&1&0 \\
0&0&1&1&0&0 \\
0&0&1&0&0&0 \\
\end{pmatrix} ,
\begin{pmatrix}
0&3&0&1&0&0 \\
3&0&1&0&0&0 \\
0&1&0&2&1&1 \\
1&0&2&2&1&0 \\
0&0&1&1&0&0 \\
0&0&1&0&0&2 \\
\end{pmatrix}
Soldaki bitişiklik matrisinin köşegeni sıfırdır ve matris simetriktir. Sağda ise simetri olmasına rağmen, ağ kendine bağlantı içerdiği için köşegeni sıfır değildir. Kendine bağlantıları içeren köşegen değerlerinin neden 1 değil de 2 olduğu bize, ağlardaki bağlantı türlerinin en başta iki gruba ayrılacağını söyler.
Yönsüz Ağlar ve Yönlü Ağlar
Ağ biliminde bir sistemin ağ yapısı altında incelenmesinde ilk belirlenmesi gereken ağın yönsüz mü yoksa yönlü mü olduğudur. Yönsüz ağlar NN adet düğüm ve EE adet çift yönlü kabul edilen bağlantı ile G=(N,E)G=(N,E) şeklinde tanımlanır. Örneğin yukarıdaki şekilde 1 ve 4 düğümleri arasındaki bağlantı çift yönlüdür (↔↔ şeklinde düşünülebilir). Yönsüz ağlarda kendine bağlantı varsa, bağlantı yine çift yönlü olduğu için ilgili düğümün matris köşegen değeri 2 olmaktadır.
Yönlü ağlarda ise bağlantılar tek yönlüdür. Yönlü bağlantılar olarak da adlandırılırlar ve uçlarında ok işareti olan çizgiler ile gösterilirler (→→). NN adet düğüm ve EE adet tek yönlü bağlantı ile yine G=(N,E)G=(N,E) şeklinde tanımlanırlar. Yönlü ağlarda bitişiklik matrisinin elemanları şöyle tanımlanır:
Aij={1,i’den j’ye bag˘lantı var0,i’den j’ye bag˘lantı yok A_{ij} = \begin{cases}
1, &\text{i'den j'ye bağlantı var} \\
0, &\text{i'den j'ye bağlantı yok }
\end{cases}
G=(N,E)G=(N,E) olarak ifade edilen yönlü ağlarda düğümlerin kümesi N=N(G)N=N(G), bağlantıların kümesi ise E=E(G)E=E(G) şeklinde tanımlanır. s1∈Ns_1 ∈ N düğümünden s2∈Ns_2 ∈ Ndüğümüne giden e ∈Ee ∈ E bağlantısında s1s_1, ee'nin kuyruğu, s2s_2 ise ee'nin başıdır. Eğer ağ çoklu bağlantılar içermiyorsa s1s_1 ve s2s_2 arasında birden fazla bağlantı olamaz ve tek bağlantı s1s2s_1s_2 şeklindedir. Ağ biliminde yönsüz ve yönlü ağlara aşağıdaki örnekler verilebilir:
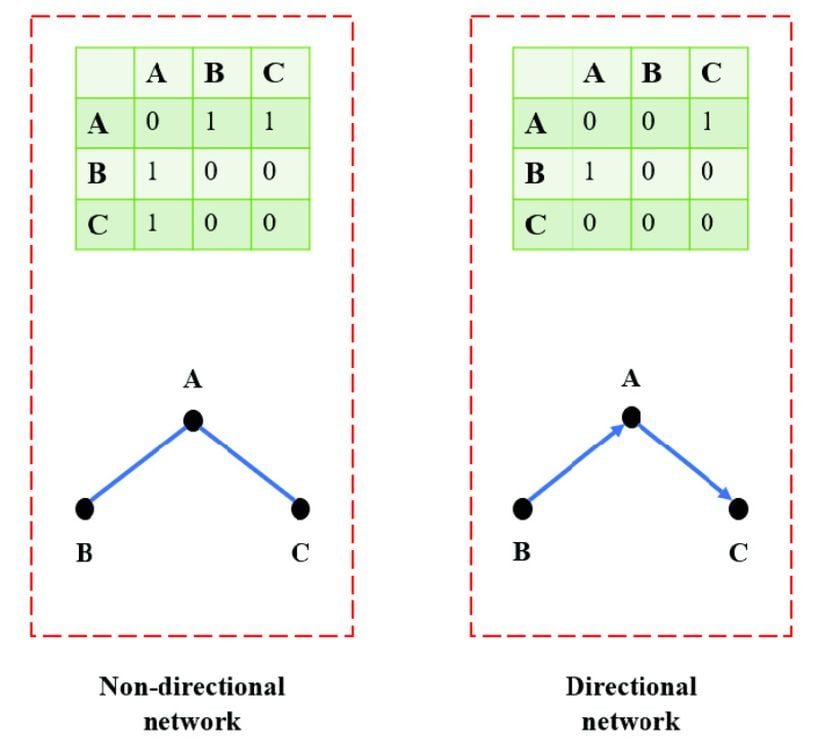
Doğada ve geliştirdiğimiz teknolojilerde, yönlü ağlar ile ifade edilebilecek sistemlerin sayısı oldukça fazladır. Yönsüz ağlardaki gibi, yönlü ağlarda da çoklu bağlantılar ve kendine bağlantılar olabilir. Ancak kendine bağlantılarda artık çift yönlülük olmayacağından bitişiklik matrisinde ilgili köşegen değeri 1 olmalıdır. Bununla birlikte yönsüz ağların bitişiklik matrisleri simetrikken yönlü ağlarınki simetrik olmak zorunda değildir.
Ağırlıklı Ağlar
Ağ biliminde buraya kadar yönsüz veya yönlü ağlarda, düğümler arası bağlantıların hep var olup olmamaları ile ilgili durumlara değindik. Ancak bazı durumlarda bağlantılar gerçel sayılar kümesinde bazı değerler alırlar. Her bir bağlantı için 1 veya diğer pozitif tamsayılardan olma zorunluluğu yoktur. Buna bağlantının ağırlığı, büyüklüğü veya kuvveti denilebilir. Bu tip bağlantılar içeren ağlara ağırlıklı ağlar denir. Gösterimlerinde bağlantının büyüklüğüne göre kalınlığı oranlanmıştır. Yönsüz ve yönlü ağ yapıları ağırlıklı olabilir.
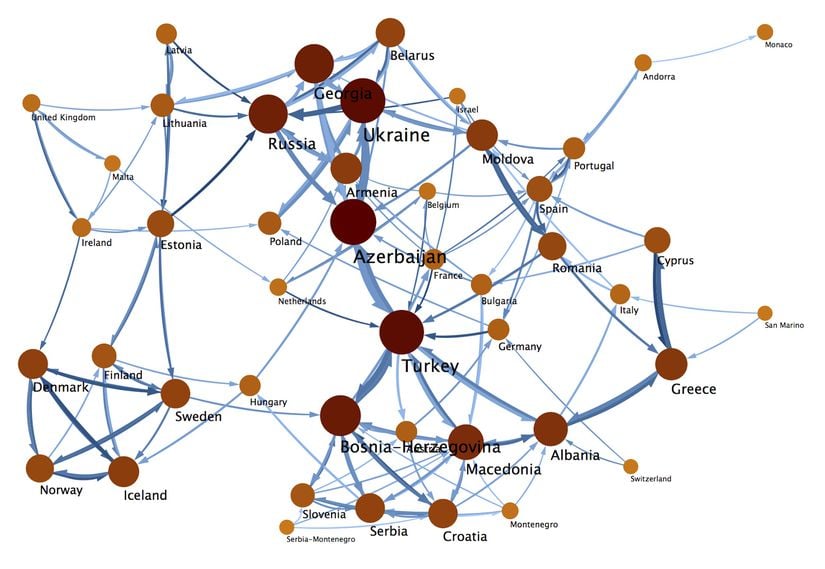
Ağırlıklı ağlar için örnek bir bitişiklik matrisi şöyle olabilir:
A=(021200.511.50)A = \begin{pmatrix}
0 &2&1 \\
2 & 0&0.5\\
1&1.5&0
\end{pmatrix}
Bir ve ikinci düğümler arasındaki bağlantının (Matrisin 1. satır, 2. sütun değeri veya tam tersi olan 2. satır, 1. sütun değeri) 1. ve 3. düğümler arasındakinden iki kat, 2. ve 3. düğümler arasındakinden dört kat daha büyük olduğunu görebiliriz.
Ağırlıklı ağlar için tüm topolojik ve dinamik hesaplar, ilgili eşitliklere bağlantı ağırlığının eklenmesiyle farklılaşır. Bununla birlikte ağırlıklı bağlantılar, çoklu bağlantılar şeklinde ifade edilerek çoklu bağlantılı bir ağa dönüştürülebilir. Ağırlıklı olarak modellenen bazı ağlarda ağırlıksız bağlantılara normalizasyon da mümkündür.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
İçerikle İlgili Sorular
Soru & Cevap Platformuna Git- 6
- 1
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- M. E. J. Newman. Networks: An Introduction. ISBN: 9780199206650.
- M. E. J. Newman. (2004). Analysis Of Weighted Networks. Physical Review E, sf: 056131. doi: 10.1103/PhysRevE.70.056131. | Arşiv Bağlantısı
- K. T. Huber, et al. (2006). Phylogenetic Networks From Multi-Labelled Trees. Journal of Mathematical Biology, sf: 613-632. doi: 10.1007/s00285-005-0365-z. | Arşiv Bağlantısı
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 20/04/2024 12:26:25 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12774
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.





