Yıldızlarda Minimum ve Maksimum Kütle Limiti

- Özgün
Yıldızlar herhangi bir kütle değerine sahip olamazlar. Bu nedenle yıldızlarda minimum ve maksimum kütle sınırları bulunmaktadır. Çoğunlukla bir yıldız olabilmek için gerekli minimum kütlenin var olması gerektiği bilinir. Çünkü kütle yetersizce kahverengi cüce veya gezegen hatta daha küçük gök cisimleri oluşmaktadır. Fakat aynı zamanda yıldızlarda maksimum kütle limiti de vardır.
Yıldızların yaşantısını, en temelde onların kütlelerinin belirlediğini biliyoruz. Kütle ne kadar fazla ise o kadar kısa bir ömür, kütle ne kadar az ise o kadar uzun bir ömür sürerler. Elbette bu durum, yakıtlarını ne kadar hızlı yaktıklarıyla alakalıdır ve bu da kütleyle doğrudan bağlantılıdır. Dolayısıyla yakıtı yakamayacak kadar az kütleye sahipse yıldız olamaz, çok fazla kütleye sahipse de şartlar biraz fazla ekstrem bir hal alır ve stabil bir yıldız olarak kalması zorlaşır.
Yıldızlarda Minimum ve Maksimum Kütle Değerleri
Yıldızlarda Minimum Kütle Değeri
Yıldız olmanın temel koşulu olan çekirdekte bir nükleer füzyonun başlaması, belirli bir kütle değerinin üzerinde mümkündür. Temelde hidrostatik denge denkleminden yola çıkarak elde ettiğimiz Virial teoremi, bize kütle çekim ile termal enerji (ısısal enerji) arasındaki bağlantıyı verir. Virial teoreminin söylediği üzere, kütle çekimsel potansiyel enerjinin yarısı içerideki gazı ısıtmak üzere termal enerjiye dönüşür. Nükleer füzyon tepkimelerinin başlaması belirli bir sıcaklık değeri gerektirdiğinden, buradan açıkça görüyoruz ki nükleer füzyonu başlatmak için gerekli bir minimum kütle değeri vardır. Çünkü yıldızın ne kadar çökeceğini, dolayısıyla merkezinin ne kadar sıcak olacağını, onun başlangıç kütlesi belirler.
Nükleer tepkimeler sıcaklığa aşırı duyarlı olduğundan bizim belirlediğimiz bu minimum kütle değeri esasında bir kabule dayanır. Yıldız olarak kabul etmediğimiz kahverengi cüceler de merkezlerinde bir takım nükleer tepkimeler gerçekleştirebilir. Fakat kahverengi cücelerde nükleer tepkimelerin gerçekleşme olasılığı oldukça düşüktür, deyim yerindeyse cayır cayır yanmamaktadırlar. Bu sebeple minimum kütle değerinin hemen altında kahverengi cüceler yer alır.
Yıldız olmak için gerekli bu minimum kütle değeri 0.084 Güneş kütlesine eşittir. Yapılan bu teorik hesabı ilk olarak NGC 6397 küresel kümesi üzerinde yapılan gözlemler desteklemiştir. Ancak, eğer yıldızın oluştuğu bulutsu, hidrojen ve helyum haricindeki ağır elementler (demir, bakır, karbon, silisyum vs.) bakımından zengin ise, 0.075 Güneş kütlesi de bir yıldız olmak için yeterli hale gelebilir. Bir bulutsunun ağır elementler (astronomlar hidrojen ve helyum hariç tüm elementlere “metal” ya da "ağır element" der) açısından zengin kabul edilebilmesi için, o bulutsuyu oluşturan maddenin %2 veya %3’ünün bu elementlerden oluşuyor olması yeterlidir.5
Maksimum Kütle Değeri
Hidrostatik dengedeki bir yıldızda kütle çekim kuvveti ile basınç kuvveti birbirini dengelemiş durumdadır. Bu denge denkleminden görüyoruz ki, kütle ne kadar fazla ise basınç kuvveti de o kadar fazla olacaktır. Burada basınç kuvveti olarak ifade ettiğimiz kuvvet, temelde gaz ve ışıma (radyasyon) basıncının toplamı olarak ifade edilir. Gaz basıncı ve ışıma basıncı doğrudan sıcaklık ile ilişkilidir, fakat nükleer tepkimeler sıcaklığa daha duyarlı olduğundan ışıma basıncı sıcaklığa daha da duyarlıdır. Ayrıca kütle arttıkça, kütlenin daha büyük bir bölümü çekirdekte toplanacağından, tepkime olasılığı daha yüksektir. Pgaz ∝ T ve Pışıma ∝ T4. Yani sıcaklık 2 katına çıktığında gaz basıncı da 2 katına çıkar, fakat ışıma basıncı 16 katına çıkar.
Dolayısıyla kütlenin fazla olması sıcaklığı artıracak, bu da basıncın artmasına ve kütle çekimine karşı koymasına sebep olacaktır. Ne kadar fazla kütle eklenirse, ışıma basıncı da ona karşı ciddi miktarda artacağından, yıldız dışarıya doğru, içten gelen, daha büyük bir kuvvet uygulamaya başlar. Kütle çekime zıt yönlü ve daha büyük bir basınç kuvveti oluşması, yıldızı dağılma durumuyla yüz yüze getirir. Dolayısıyla yıldızın varlığını sürdürebilmesi için bir maksimum kütle değeri bulunmalıdır.
Bu kütle değeri gerekli hesaplamalar yapıldığında 1.8 x 1032 kg ya da bir başka deyişle 90 Güneş kütlesi kadar bulunur. Bu bazı kaynaklarda yapılan hesaplamalar 120-150 Güneş kütlesine kadar çıkmaktadır. Fakat yapılan bu teorik hesapların aksine yapılmış gözlemlerde çok daha büyük kütleli yıldızlar gözlendi. Bugün bilinen en büyük kütleli yıldız R136a1 yıldızıdır ve 265 Güneş kütlesine sahiptir. Son zamanlarda yapılan bir çift yıldız gözleminde iki adet büyük kütleli yıldızın birleşmekte olduğunun görülmesi sonucunda, bu devasa kütleye sahip yıldızların çiftli sistemlerin birleşmesi sonucunda oluştuğu düşünülmeye başlandı.1
İleri Okuma ve Teorik Hesaplar
Minimum Kütle Değerinin Elde Edilmesi
Bir yıldız için minimum kütle değeri, en düşük sıcaklıkta gerçekleşen nükleer füzyon tepkimesi olan hidrojenin yanmasının sürdürülebilir olmadığı kütle limitidir.
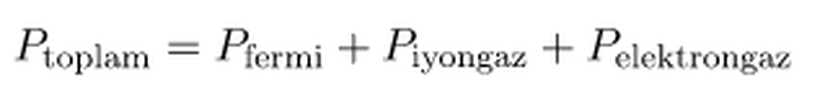
Küçük ve soğuk gaz küreleri için toplam basınç, yukarıdaki şekilde üç ayrı basıncın toplamı olarak ifade edilir.
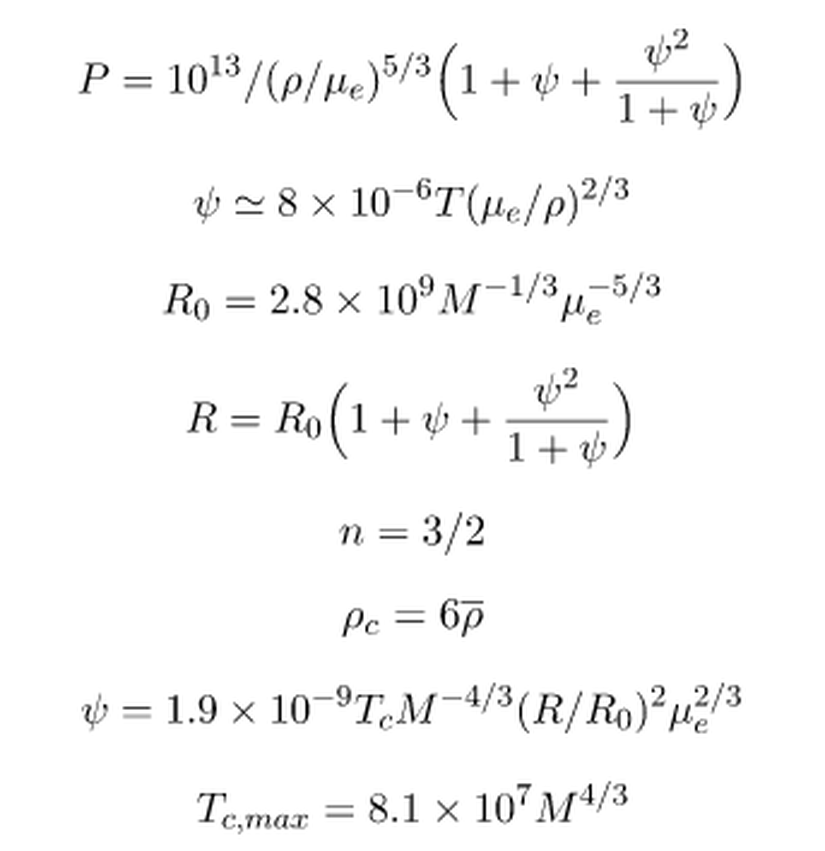
Hidrojenin füzyonu, 3 x 106 Kelvin sıcaklığın üzerinde sürdürülebilir olduğundan, yıldızlar için minimum kütle değeri Mmin=0.084 Güneş kütlesi olarak bulunur.2
Maksimum Kütle Değerinin Elde Edilmesi
Bir noktada radyasyon basıncı, gaz basıncı ile kıyaslanabilir hale gelir ve radyasyon basıncının çok artması, yıldızın dağılmayla yüzleşmesine sebep olur. Denge için gerekli koşulun
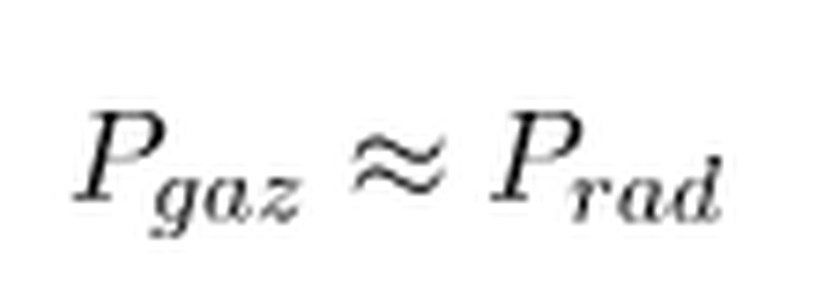
olduğunu ele alacak olursak,
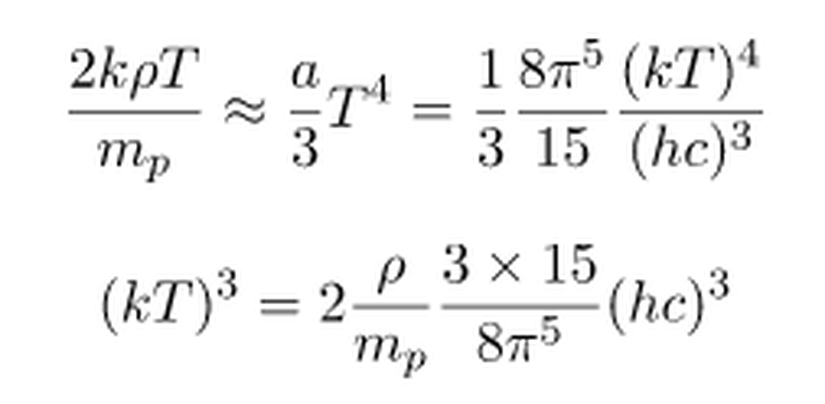
Kütle çekim ile gaz basıncı arasındaki dengeleyici durum
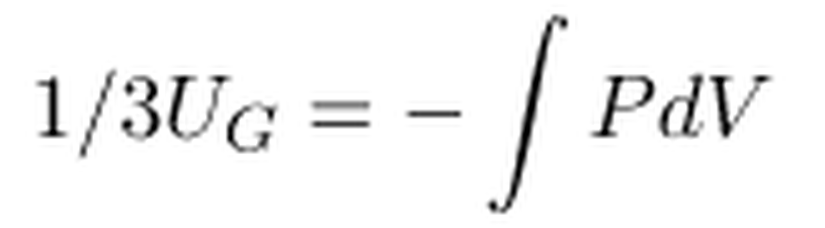
olduğuna göre,
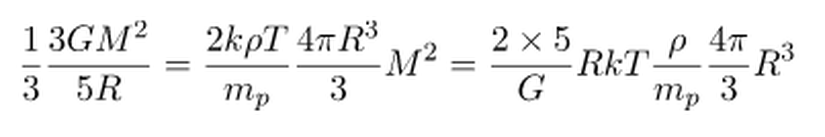
Buradan çözdüğümüzde,
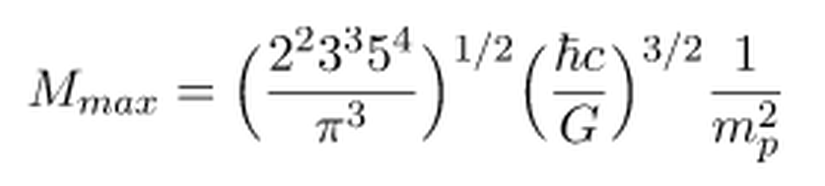
Denklem şu noktada sadece doğa sabitlerine bağlı hale gelir ve sonuç hesaplandığında 90 Güneş kütlesi olarak bulunur. Fakat yüzlerce hatta binlerce Güneş kütlesine sahip model hesaplamaları da bulunmaktadır.2
Hazırlayan: Ögetay Kayalı
Referanslar
1. MY Camelopardalis, a very massive merger progenitor
<https://arxiv.org/abs/1410.5575>
2. K. S. De Boer & W. Seggewiss, Stars and Stellar Evolution, Stellar Structure, p. 90-91
3. Paul R. Woodward, Theoretical Models of Stars Formation,
<http://www.annualreviews.org/doi/pdf/10.1146/annurev.aa.16.090178.003011>
4. <http://hypertextbook.com/facts/2001/KellyMaurelus.shtml>
5. Gilles Chabrier & Isabelle Baraffe, Structure and Evolution of Low-Mass Stars
<https://arxiv.org/pdf/astro-ph/9704118v1.pdf>
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 20/04/2024 13:41:13 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12934
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.


