Yıldız Astrofiziği: Disk Oluşumu

- Özgün
Evrende gördüğümüz birçok yapı, disk şeklinde bulunmaktadır. Bu disk oluşumu çok temel fizik yasalarının sonucunda gerçekleşir. Bu disk benzeri yapılardan belki de en dikkat çekici olanı spiral (sarmal) galaksilerken, Güneş sistemi gibi yıldız sistemlerindeki gezegenler de yıldızın doğumu sırasında oluşan bir disk üzerinde doğmuştur.
Böylesine disk benzeri yapıların görülmesinin ardındaki fiziksel sebep, gündelik hayattan da tecrübe ettiğimiz bir etkiye dayanır: Merkezkaç etkisi. Arabayla hızla giderken, aniden bir virajdan döndüğünüzde, adeta yan taraflara savrulursunuz. Burada hissettiğiniz şey, aslında eylemsizliktir. Hareketinizin bir vektörü (yönü) vardır ve vektörler daima doğrusaldır. Fakat dönüş yaptığınız için vektörünüzün yönü değişmektedir. Eylemsizlik ise, tam olarak sizin mevcut hareket vektörünüzü korumak istemenizdir. Bu sebeple vektör değiştikçe, siz de savrulmayı hissedersiniz.
Evrende dönmeyen bir yapıya rastlamak neredeyse imkansızdır, çünkü her şeyin, bir şekilde hareketi vardır. Hiçbir şey sabit değildir. En ufak bir başlangıç hareketi, tüm sistemin bir çalkantı yaşamasına sebep olur. Bu yüzden evrenin her yerinde hareketli yapılar görmek pek de şaşırtıcı değildir.
Disk Oluşumu Fiziği
Yeterli kriterlere sahip gaz ve toz bulutlarının, çökerek yıldızları oluşturduğunu biliyoruz (bkz. Hidrostatik Denge). Aslında gördüğümüz tüm cisimler, bir şekilde kütle çekimsel topaklanmaların bir ürünüdür. Bir devasa gaz ve toz bulutu ele alalım. Bu gaz ve toz bulutunun içerisindeki parçacıklar bir şekilde harekete sahipler. Bulut, çok yavaş da olsa bir dönme hareketi yapıyor. Bulut, zamanla çökmesine devam ettikçe, dönme hızı artacaktır. Bu durum, buz pateni yapanlarda gördüğümüz durumla aynı prensibe dayanır.
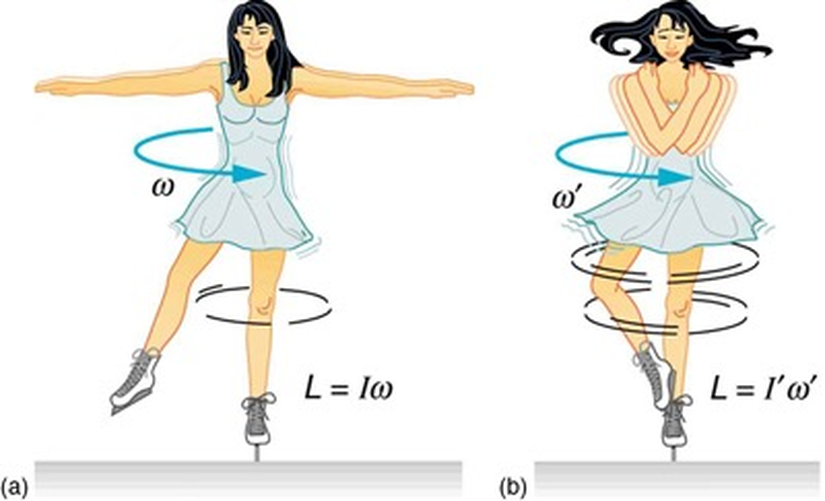
Buz patencisi kolları açıkken var gücüyle döner ve ardından kollarını kapatır. Kollarını kapatmasının ardından patenci daha da hızlı dönmeye başlar! Bulutlarda da gerçekleşen şey tam olarak budur. Olay, açısal momentumun korunumuna dayanır. Kollar açık haldeyken sahip olunan açısal momentum L1, kollar kapalıyken sahip olunan açısal momentuma L2 eşit olmalıdır.
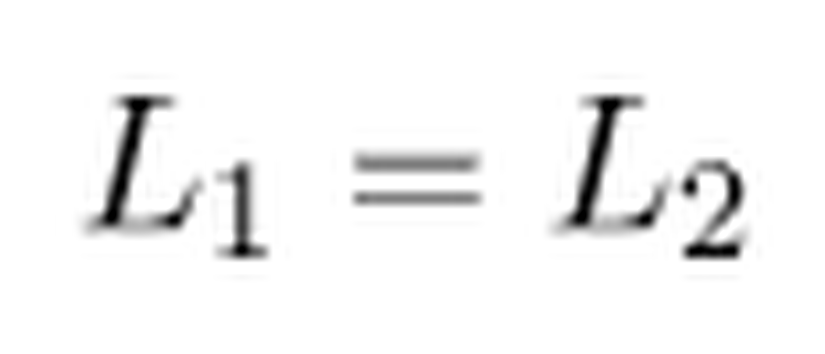
Açısal momentumu, eylemsizlik momenti I ve açısal hız ω cinsinden aşağıdaki gibi ifade ederiz.
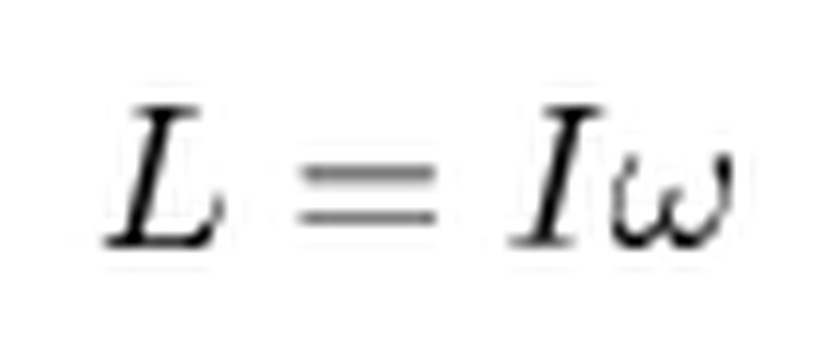
Eylemsizlik momenti de I=mr2 olduğuna göre, açısal momentumu, kütle, yarıçap ve açısal hız cinsinden aşağıdaki gibi ifade edebiliriz.
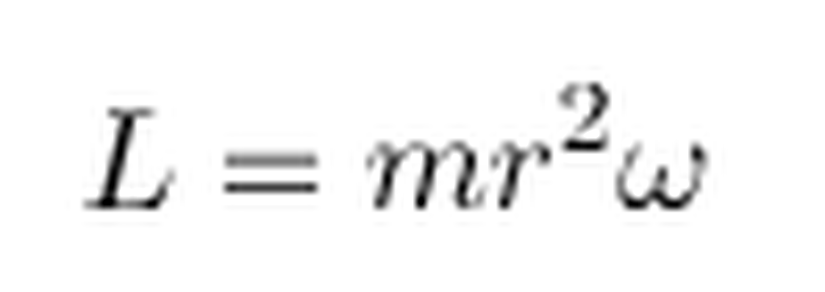
Şimdi bir kıyaslama yapabiliriz. Bildiğimiz şey kütlenin değişmediği, yarıçapın azaldığı ve açısal momentumun korunması gerektiği. İlk durumdaki yarıçapa r1, açısal hıza w1 dersek,
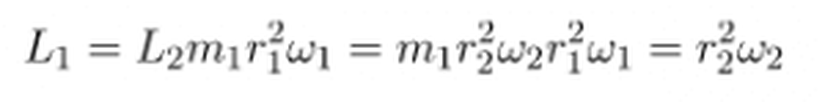
Çökme gerçekleştiği için r1>r2 olduğunu biliyoruz. Bu durumda eşitliğin sağlanabilmesi için ω1 < ω2 olmalıdır. Bu da çökmekte olan bir cismin, açısal momentumun korunumu gereği, giderek hızlanması gerektiğini gösterir.
Çökmekte olan bir bulut, giderek daha hızlı döneceği için, dönme düzlemi üzerinde merkezkaç etkileri baskın hale gelecektir. Normalde bir yıldızın oluşumu sırasında çökmekte olan bulutun kütle çekim kuvveti, giderek sıkıştırdığı gazın artan basıncının oluşturduğu basınç kuvveti ile dengelenerek, küresel bir yapıda dengeye gelir. Fakat işin içerisine ek bir kuvvet girdiğinde, simetri bozulur. Örneğin çok hızlı bir dönme gerçekleşiyorsa yıldız, en hızlı dönmenin gerçekleştiği ekvator düzleminden dışarıya doğru şişecektir. Çünkü artık merkezcil ivmeden gelen üçüncü bir etki söz konusudur ve bu etki en çok ekvator bölgesinde hissedilir.
Yıldız oluşumu sırasında oluşan disk de tam olarak bu sebeple buradadır. Bu disk, merkezdeki yıldızın dönüş düzlemi üzerinde oluşur. Ekvatordan kutuplara doğru gidildikçe, merkezcil ivmenin payı azaldığından, burada bulunan madde yıldızın üzerine doğru çöker. Fakat dönüş düzlemindeki materyal, kuvvetler dengesi sağlandığından, olduğu yerde kalır. Bu sayede burada kalan materyaller, zaman içerisinde öbeklenerek gezegenleri oluşturur. Burada bu diskin bir kalınlığı olacağına da dikkat edin. Bu yüzden gezegenler, Güneş'in dönme düzlemine çok yakın düzlemlerde yörüngelere sahiptir. Fakat ufak da olsa açısal farklılıkları vardır, çünkü diskin de bir kalınlığı vardır. Kaba bir yaklaşımla tüm yörüngeler, bu diskin kalınlığı içerisinde kalır denebilir.
Burada düşünmenizi istediğim ucu açık bir soruyla sizleri baş başa bırakmak istiyorum. Bu etkiyi hangi boyutlarda (ölçekte) görebiliriz? Bu yazıda galaksilerde ve yıldız sistemlerinde gördüğümüzden bahsettik. Peki ya daha büyük ölçekte? Örneğin galaksi kümeleri de disk benzeri bir yapı oluşturuyor mu? Onlarda durum sanki daha küresel gibi görünüyor, sizce bu farklılığı oluşturan şey ne olabilir?
Hazırlayan: Ögetay Kayalı
Referanslar
1. Melike Afşar, Ege Üniversitesi Astronomi ve Uzay Bilimleri Bölümü, Solar System Ders Notları
2. <http://ffden-2.phys.uaf.edu/webproj/211_fall_2014/Ariel_Ellison/Ariel_Ellison/Angular.html>
3. <http://physics.bu.edu/~redner/211-sp06/class-rigid-body/figureskater.html>
4. <http://physics.highpoint.edu/~atitus/videos/AngularMomentumPrinciple/figure-skater-spin/figure-skater-spin.pdf>
5. <http://www.wskc.org/documents/281621/309188/ENGAGE_Physics_FigureSkater.pdf/819a760e-54c6-46c9-a9fc-5f9f8d442d22>
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 25/04/2024 23:32:16 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12614
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.


