Bütün yıldızların, gaz ve toz bulutlarının, kendi kütle çekimleri altında çökerek oluştuklarını biliyoruz. Çökme süresi, kabaca bu çökmenin meydana geleceği yaklaşık zamanı ifade eder. Kütle çekim, gerekli koşullara sahip bir gaz bulutunun, kendi üzerine çökmesini sağlamak için yeterli bir kuvvettir. Bunun yanında süpernova patlaması sırasında çıkan şok dalgası gibi bazı tedirginliklerin de yıldız oluşumunu destekleyebileceği düşünülmektedir. Fakat bu kesinlikle bir gereklilik değildir, aksi takdirde ilk yıldızların oluşumunu açıklamakta bir hayli zorlanırdık. Zaten kütle çekimin yeterli koşulları sağlamadığını düşünmek için hiçbir geçerli nedenimiz yok.
Virial teoremi üzerinden hareketle Jeans kriterlerini tanımlamıştık. Eğer sistem, Jeans kriterlerinde belirtilen yeterli koşulları sağlıyorsa kendi üzerine çökecektir. Bu çöküşü biraz daha detaylı anlayabilmek için, böylesi bir sistemin kendisi üzerine çökme süresini incelemeliyiz. (Bkz. Virial Teoremi)
Çökme Süresi Denklemi
Çökme süresi, aşağıdaki şekilde ifade edilir.
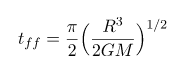
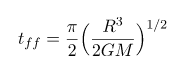
Başlangıçta denkleme baktığımızda bu denklem, yarıçap ve kütleye bağlı görünüyor. Fakat bu iki parametre aslında tek bir parametreyi işaret eder; o da yoğunluktur.
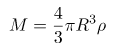
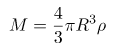
Küresel bir hacme sahip cisim için kütle, yukarıdaki gibi ifade edilir. Burada küresellik varsayımı yaptığımızı es geçmeyin. Normalde büyük gaz ve toz yapıları dağınıktır ve küresel değildir. Fakat fizikte, bazı çıkarımlar yapabilmek için bazı kabullenmeler yapmalıyız. Daha detaylı analizlerde daha farklı metotlar izlenmesi gerekecektir, burada sadece basit bir yaklaşım yapıyoruz.
Bu ifadeyi yerine koyarsak, çökme süresi için aşağıdaki eşitliği elde ederiz.
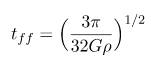
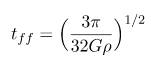
Böylelikle görüyoruz ki, bir gaz ve toz bulutunun çökme süresi, onun yalnızca başlangıç yoğunluğu ile alakalı. Burada dikkat edilmesi gereken bir diğer nokta da budur. Çöktükçe yoğunluğunun değişeceğini unutmayın. Buradaki yoğunluk ifadesi, bulutun, incelediğimiz andaki başlangıç yoğunluğunu ima eder.
Yoğunluk ifadesi, paydada yer aldığına göre, yoğunluk arttıkça, çökme süresi kısalacaktır, ki bu da beklediğimiz bir şeydir. Daha yoğun bir gaz ve toz bulutunun daha kısa sürede çökecek olması, akla yatkın geliyor. Çünkü çökmeye sebep olan şey kütle çekimin kendisidir. Yoğunluğun fazla olması da yeteri kadar maddenin, birbirine yeteri kadar yakın olduğunu söyler. Bu da kütle çekimin kısa sürede yanıt vermesi demektir.
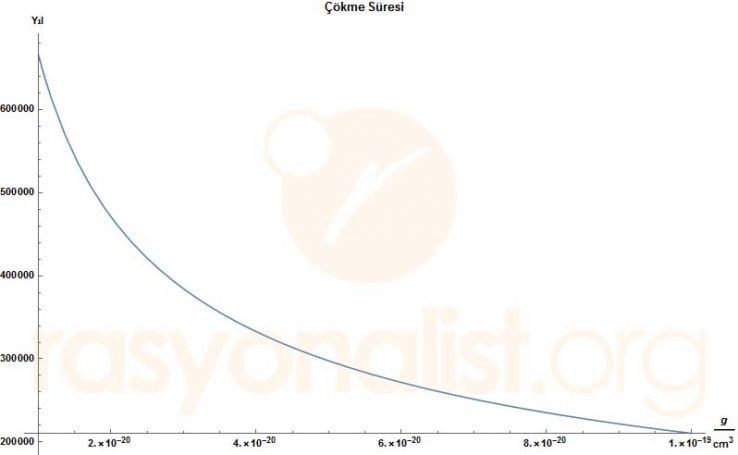
Jeans kriterleri, bulutun çökme koşullarını belirlediğine göre, Jeans yoğunluğunu bu eşitlikte yerine koyarak, bir bulutun çökme süresini bulabiliriz. 20 K sıcaklığındaki bir bulutun Jeans yoğunluğu, 1 Güneş kütlesi için 10-19 g cm-3 olduğuna göre, bu Jeans yoğunluğuna sahip bulut için yıl cinsinden çökme süresinin yoğunluğa bağlı grafiği aşağıdaki gibidir. (Bkz. Jeans Kriterleri)
Ögetay Kayalı
Referanslar
1. Melike Afşar, Ege Üniversitesi Astronomi ve Uzay Bilimleri Bölümü, Solar System Ders Notları
2. K. S. De Boer & W. Seggewiss, Stars and Stellar Evolution
3. <http://csep10.phys.utk.edu/OJTA2dev/ojta/c2c/starbirth/recipe/criterion_tl.html>
4. <http://www.astro.uu.se/~hoefner/astro/teach/apd_files/apd_collapse.pdf>