Önünüzde tavadan yeni aldığınız, üstünde dumanları tüten, lezzetli mi lezzetli krepimiz olsun. Elbette yemek için dilimlememiz gerekecek, ama dilimlemeyi en iyi şekilde yapmak istiyoruz. Öyle bir dilimleyelim ki, her dilimleme işlemi sonucunda önümüzde, olabilecek en fazla sayıda dilim olsun.
Akla ilk gelen, her seferinde tam ortadan ikiye bölme yöntemi bu konuda maalesef başarısız. Bu yüzden bu sayı dizisine, tembel şefin dizisi deniyor (aynı zamanda merkezcil poligonal sayılar da denilir). Çünkü dilimlemeyi, abuk subuk yapmanız gerekiyor. Yani en azından, gözümüze pek estetik görünmeyecek, adaletli dilimler ortaya koymayan bir yöntem. Fakat sonucunda ortaya çıkan sayı dizisi, oldukça basit bir dizi. Böylesine basit bir sayı dizisinin, fiziksel bir anlam taşıyor olması, aslında matematiğin ne denli harika bir araç olduğunu bir kez daha gösteriyor.
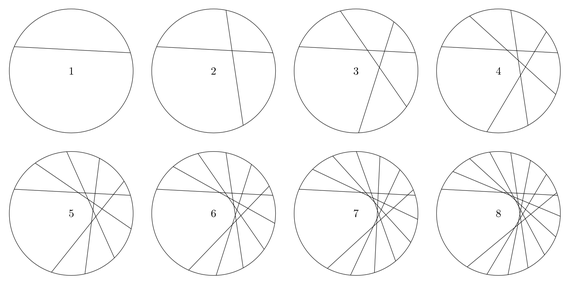

En çok sayıda dilim elde etmek için yapmamız gereken aslında basit bir algoritma var. Yukarıdaki örnekte çember üzerine çizilen doğrularla, çeşitli parçalara bölüyoruz. İlk doğru, ne olursa olsun iki parçaya bölecektir. İkinci doğru ise bu doğru ile bir noktada kesişebilir veya kesişmeyebilir. Kesişmezse üç, kesişirse dört parça çıktığına dikkat edin. Üçüncü doğruyu koyduğumuzda ise, işin sırrı ortaya çıkmaya başlıyor. Diğer iki doğruyu kesen bir doğru tanımlıyoruz. Dördüncü için de diğer üç doğruyu kesen bir doğru… Yani her tanımladığımız doğru, önceki doğruların hepsini bir noktada kesmeli. Bu yüzden sondaki şekil gibi farklı bir desen ortaya çıkıyor. Çünkü kesişimi sınırlı bir açı aralığında sağlayabiliyoruz.


Tembel Şefin Dizisi
İşin geometrik yorumu, sayısal yorumundan çok daha zor. Fakat ardında öyle basit bir matematik var ki bunun üç boyutlu halini dahi basit bir hesapla bulabiliyorsunuz. Her hamlede elimizde kaç dilim olduğunu sırayla yazalım. İlk başta turtamız bir bütün olduğu için 1, ardından bölerek 2, tekrar bölerek 4… Yani aşağıdaki sayı dizisinde dilim sayıları elde ettik.
![]()
![]()
Sıradaki sayıyı tahmin etmeye çalıştığınızda fark edeceğiniz şey, bu sayı dizisinin basit bir artış gösterdiği olacaktır. Eğer bu dizinin nasıl arttığına bakacak olursak ve bununla yeni bir dizi ifade edersek, şu basit diziyle karşılaşırız. (2’den 1’i çıkarın, 4’ten 2’yi, 7’den 4’ü…)
![]()
![]()
Dolayısıyla sıradaki sayıyı tahmin etmek oldukça basit. Sıradaki eklenmesi gereken sayı 6 olduğu için, 16+6‘dan, sıradaki dilim sayısını 22 olarak bulabiliriz. Bu sayı dizisinin de fiziksel bir anlamı var aslında. Bir doğru parçasını, noktalar ile parçalara bölüyoruz. Nasıl bizim örneğimizde bir yüzeyi, doğrular ile bölüyorduysak, bunda da boyutlarımızı birer azaltarak işlem yapıyoruz. Eğer bir doğru üzerinde bir nokta işaretlersem, iki ayrı doğru parçası, bir nokta daha koyarsak, üç doğru parçası şeklinde giderek artan ve bu sayı dizisini veren bir dizilim elde ederiz. Geriye doğru giderken boyut azalıyorsa, ileriye doğru giderken de boyut artıyor olabilir.
Üç Boyutta Tembel Şefin Dizisi
Şanslıyız ki üç boyutta yaşayan canlılarız ve bu bize ilk üç diziyi inceleyip, bir çıkarım yapma olanağı sağlıyor. Aksi halde elimizde yeterli veri olmayabilirdi. Yeni bir dizi tanımlayalım ve bu sefer, (1) nolu dizimizi buna ekleyerek ilerleyelim. Bu dizi 1 sayısı ile başlasın ve an dizisinin 1. elemanı buna eklensin. Bu şekilde ilerleyelim.
![]()
![]()
İlk üç işlemin (birinciden sonraki üç değerin), 2 sayısının katları olduğuna dikkat edin. Bu bizim esas dizimizde yalnızca iki taneydi, fakat burada üç tane. Orada; yüzey üzerinde doğrularla kesim yapıyorduk. Şimdi ise üç boyutta; katı bir cisim üzerinde, yüzeyler ile bölme yapıyoruz. Bir küpünüz olduğunu düşünün ve bunu keserek bölmeye başlayın. İlk hamle ile ikiye, ardından buna dik olarak keserek dörde, sonra yine bunlara dik olarak sekize bölebilirsiniz. Bundan sonra yapacağınız hamlelerin değişmesi gerekiyor.
Aslında bu bize harika bir sonuç veriyor! İkinin üssü olan bu sayıların adedi, o uzayda birbirine dik vektörlerin sayısını ifade ediyor aynı zamanda! Yani doğrudan kaç boyutlu bir uzayda olduğumuzu ifade ediyor! Bu işlemi bir adım daha öteye götürerek, hayal edemediğimiz dört boyutlu uzaydaki cismi, üç boyutlu cisimlerle en çok sayıda dilim oluşturacak şekilde nasıl bölebileceğimizi bulabiliyoruz. Çok basit bir sayı dizisi sayesinde, böylesine hayal etmesi zor bir işlemin sonucu, basitçe karşımıza çıkmış oluyor.
Formülasyon
Dilimleme sayısı n için elde edilen en çok sayıda dilim p olsun. n sıfırdan büyük eşit için,
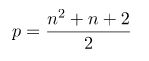
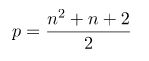
Binom katsayılarını kullanarak,
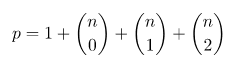
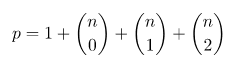
şeklinde genelleyebiliriz.
*Krep üzerinde verdiğimiz iki boyuttaki örnek için tembel şefin dizisi (lazy caterer’s sequence) ya da merkezcil poligonal sayılar (central polygonal numbers) çevirilerini yaptık. Üç boyutta geçen dizinin adı ise kek sayısı (cake number)’dır.
Ögetay Kayalı
Referanslar
1. Central polygonal numbers (the Lazy Caterer’s sequence): n(n+1)/2 + 1; or, maximal number of pieces formed when slicing a pancake with n cuts. (OEIS-A000124) <https://oeis.org/A000124>
2. Maximal number of regions obtained by joining n points around a circle by straight lines. Also number of regions in 4-space formed by n-1 hyperplanes. (OEIS-A000127)
3. Sloane, N. J. A. Sequence A000125/M1100 in “The On-Line Encyclopedia of Integer Sequences.”
