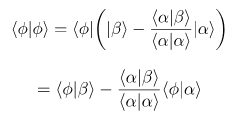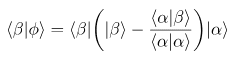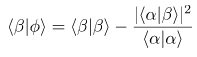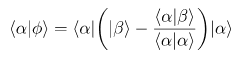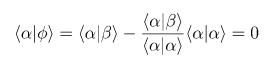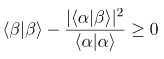Kuantum mekaniğinde sıklıkla karşımıza çıkan Schwarz eşitsizliğine dair, Griffiths’in kitabında verilen bir sorunun çözümünü ele almak istedik. Aradığınızda Schwarz eşitsizliğinin elde edilişi ile ilgili farklı notasyonlar göreceksiniz. Soruda ise aşağıdaki kalıp verilerek mevcut bilgilerimizle eşitsizliğin gösterilmesi istenmiş.
Vektörlere dair iç çarpım özelliklerini kullanarak bu eşitsizliği elde etmek mümkündür. Aşağıdaki ifadeden faydalanalım.
Ayrıca biliyoruz ki;
Eğer (2) no’lu denklemi
ile çarparsak,
Burada çıkan bilmediğimiz terimlerin ne olduğunu da yine elimizdeki (2) no’lu denklem aracılığıyla araştırabiliriz. (5) no’lu denklemden gelen
olduğundan faydalanarak (2) no’lu ifadeyi
ile çarparsak
Eşitliği açarsak
Reel ifadeler için
ifadesini kullanırsak (7) no’lu denklemi aşağıdaki şekilde düzenleyebiliriz.
Böylelikte (5) no’lu ifadede elde ettiğimiz bilmediğimiz terimlerden birini bulduk. Geriye
ifadesini bulmak kaldı.
olduğundan
İfadeyi dağıtırsak;
Şimdi (5) no’lu denklemde (7) ve (10) no’lu denklemlerden elde ettiğimiz ifadeleri yerine yazarak denklemi aşağıdaki gibi yeniden yazabiliriz.
olduğundan;
Sonuç olarak Schwarz eşitsizliği sağlanır.
Ögetay Kayalı
Referanslar
1. Introduction to Quantum Mechanics, David J. Griffiths