Project Euler 6: Karelerin Toplam Farkı
- Özgün
Soru: İlk on doğal sayının karelerinin toplamı, $1^2+2^2+3^2+...+10^2=385$ İlk on doğal sayının toplamının karesi $(1+2+3+...+10)^2=3025$ İlk on doğal sayı için toplamların karesi ile karelerin toplamı arasındaki fark $3025-385=2640$. İlk yüz doğal sayının toplamlarının karesi ile karelerinin toplamı arasındaki farkı bulun.30 Haziran 2016 itibariyle soruyu çözen kişi sayısı 316294.
Bu soru da bir önceki soru gibi matematiksel yöntemler kullanarak kağıt kalem ile rahatlıkla çözebileceğimiz sorulardan. Kod yazarak dahi basitçe bulabileceğimi bir işlem barındırıyor. Fakat burada verilmek istenen mesaj: "Bakın burada işinizi kolaylaştıracak matematiksel yöntemler mevcut. Artık doğrudan kaba çözümlerle uğraşmayın, çünkü işiniz yavaş yavaş zorlaşacak. Soruyu basit problemlere indirmeye alışmalısınız."
Bu yüzden matematiksel yaklaşımlarla soruyu yine kod yazmadan çözeceğiz. Elbette siz kod yazmayı tercih edebilirsiniz. Fakat bu soruda verilen toplamlar bir klasiktir ve sıklıkla birçok kodda da karşımıza çıkar. O yüzden ben muhakkak bu tipteki yöntemleri incelemenizi öneriyorum.
Toplamların Karesi
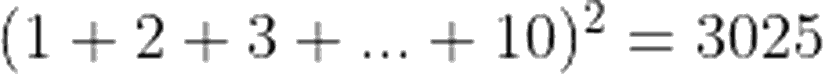
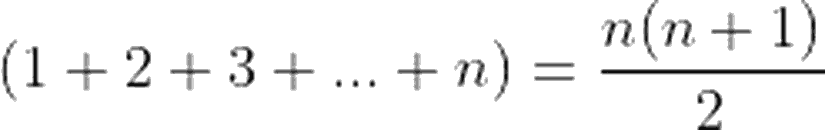
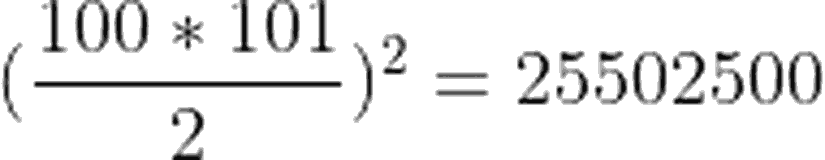
Karelerin Toplamı
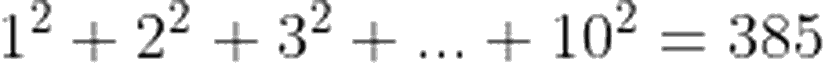
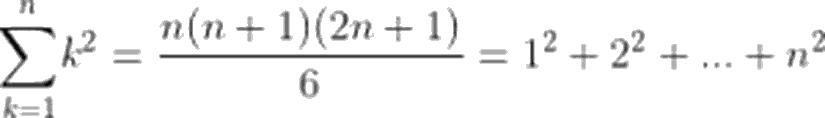
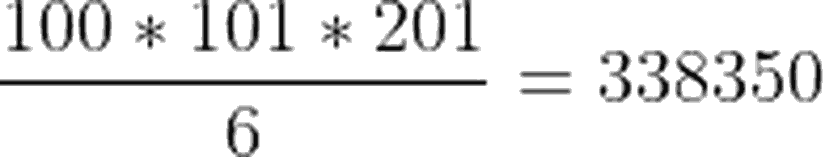
Böylelikle sonuç: 25502500-338350=25164150 olarak bulunur.
Ögetay Kayalı
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 26/04/2024 05:21:58 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12597
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.


