Project Euler 3: En Büyük Asal Çarpan

- Özgün
Project Euler 3: 13195 sayısının asal çarpanları 5, 7, 13 ve 29'dur. 600851475143 sayının en büyük asal çarpanı nedir?Project Euler 3 sorusunda karşımıza yine bir algoritma klasiği çıkıyor: Asal sayılar.
Asal sayıları elde edebileceğimiz bir sürü algoritma mevcut. Bunları incelemenizi şiddetle tavsiye ediyorum. Bir sayının asal sayı olup olmadığını denetlemenin en kaba yolu o sayıyı kendisine kadar olan sayma sayılarına bölmektir. Bu sayı bir ve kendisi hariç başka bir sayıya bölünmüyorsa asal bir sayıdır.
Fakat bu yöntem fazlasıyla gereksiz işlem kalabalığına sahiptir. Örneğin hiçbir asal sayı çift değildir, çünkü çift her sayı ikinin bir katıdır. Bu yüzden her seferinde çift sayıları kontrol etmek anlamsızdır (takdir edersiniz ki bu iki kat fazla sayının kontrol edilmesi demek). Bu soruda biz de tam olarak bu mantıktan ilerleyen bir algoritmayı ele alacağız. Lakin belirtmek isterim ki, algoritma dünyasında hızlı bir şekilde asal sayı bulmak oldukça önemli bir yere sahiptir ve bu bahsedeceğimiz algoritmalardan daha hızlıları da mevcuttur.
Eratosthenes'in Eleği Algoritması

Kareköke Kadar İncelemek
Denetlemeyi sayının kareköküne kadar olan sayılara kadar yapmak yeterlidir. Örneğin 100 sayısının asal olup olmadığını denetlemek için karekök 100'e yani 10'a kadar olan sayılara bakmak yeterlidir (bu yöntemin bizi ne kadar işlem kalabalığından kurtardığına dikkat edin). Bunun nedenini düşünmeyi size bırakıyoruz, işin arkasında oldukça şahane bir düşünce yatıyor. Eminiz elinize bir kağıt kalem alıp yazmaya başlayarak bunu kendiniz de görebilirsiniz.C# Çözümü
Eğer sayıları bir dizide kabul eder ve dizinin asal olmayan elemanlarına yanlış değerini atarsak, dizinin doğru olan elemanlarının numarası bize asal sayıları verir. Böylece kodumuz aşağıdaki şekilde olur.

Python Çözümü
Belirli bir n değerine kadar olan asal sayıları liste haline getiren fonksiyon: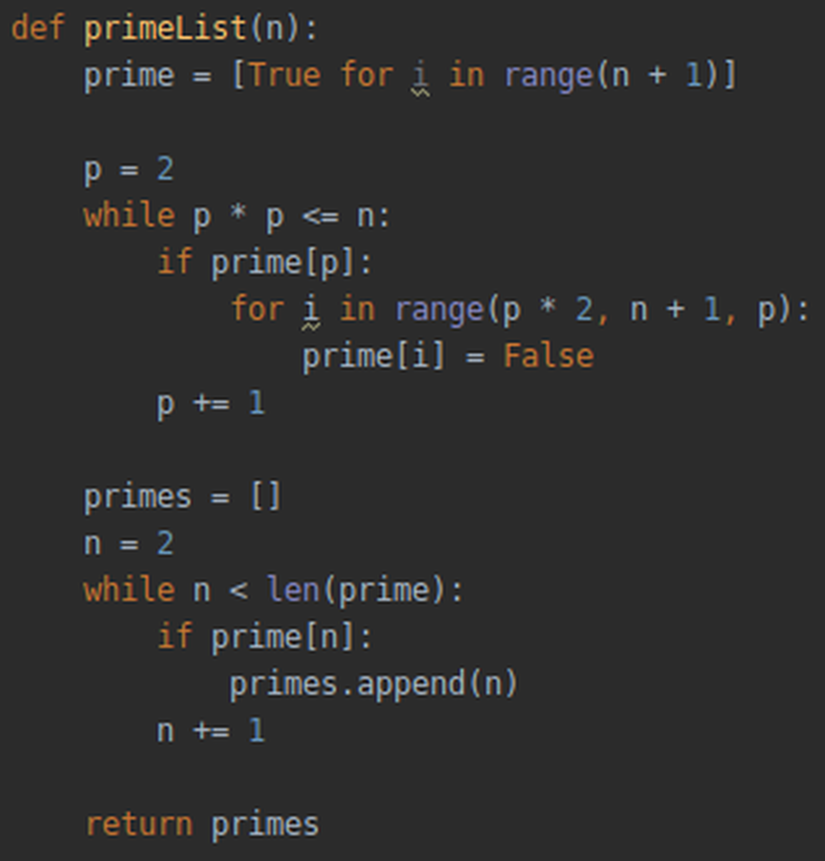
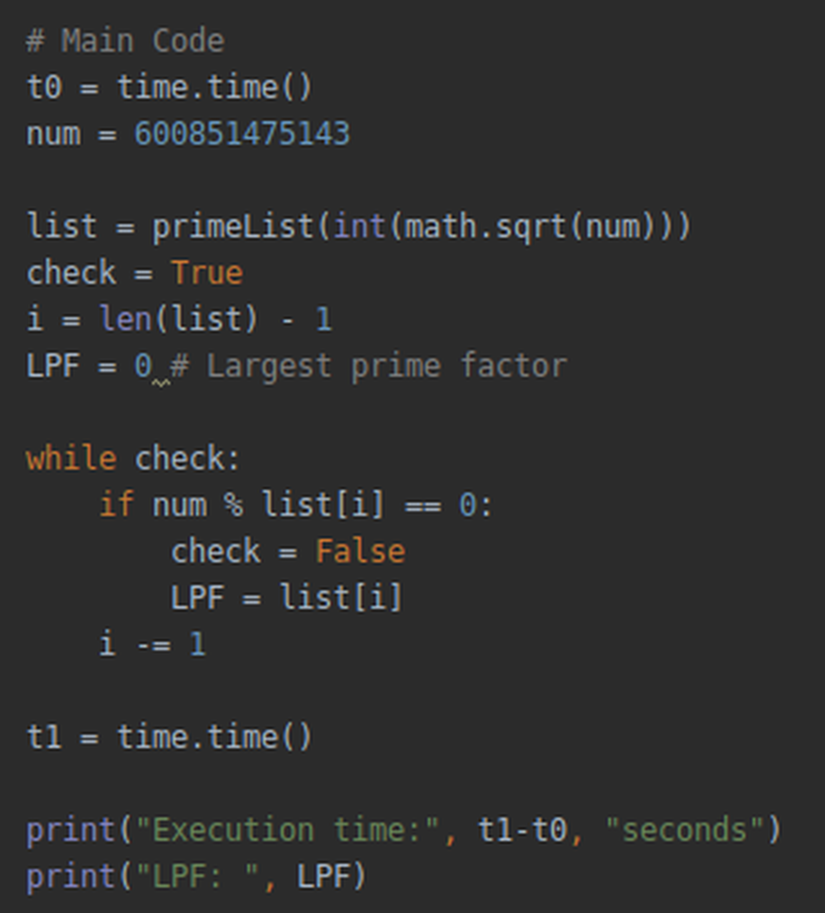

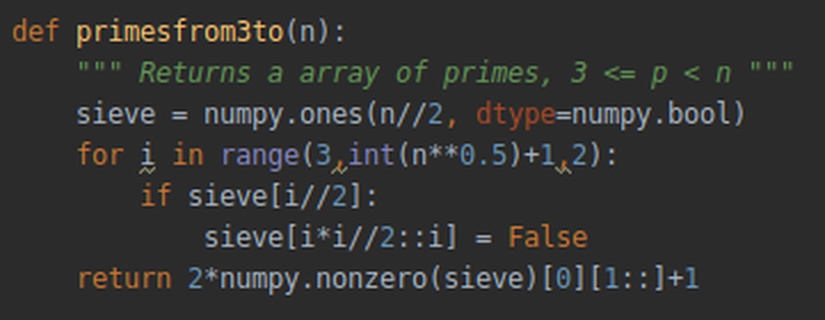
Eğer daha hızlı bir asal sayı bulma algoritması kullanırsak (ayrıca bkz.):

İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 29/04/2024 04:57:20 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12647
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.


