Project Euler 1: 3 ve 5’in Katları

Project Euler 1: Eğer 10’un altında kalan ve 3 ile 5’in katları olan bütün doğal sayıları sıralarsak: 3, 5, 6 ve 9’u elde ederiz. Bu sayıların toplamı da 23’tür. 1000’den küçük 3 veya 5’e bölünen tüm sayıların toplamları nedir?

Project Euler 1 oldukça basit bir soru. Soru numarası arttıkça soruların zorluğu da artıyor. Bu soru 30 Haziran 2016 itibariyle 574622 kişi tarafından çözülmüş durumda.

Çözüm

Bizden istenen 1000’in altında 3 veya 5’in bölenlerini bulup, bunları toplamamız. Bu soruda dikkat etmemiz gereken nokta, bize sorunun açıklamasında açıkça gösterilmemiş. 10’a kadar olan 3 ve 5’in katlarında bu iki sayının ortak katı yok. Örneğin 20’ye kadar olan sayılar için elde edeceklerimiz 3, 5, 6, 9, 10, 12, 15, 18 olacaktır. Fakat burada bir problem var! 15 sayısı hem 3’e hem de 5’e bölünüyor

Eğer yazdığınız program 3’e bölünen sayıları ayrıca topluyor, 5’e bölünenleri ayrıca topluyorsa, ortak katları iki kez toplama katacaktır. Bu da yanlış sonuç bulmanız demek. İsterseniz her ikisini ayrı ayrı toplayıp, bu genel toplamdan ortak katları da çıkarabilirsiniz.

Böyle bir yaklaşım en basit yaklaşımdır. Şu an için bir problem yok, fakat sayılar büyüdüğünde ve yapılacak işlem arttığında böylesine kaba yaklaşımlar bizim işlem süremizi aşırı uzatarak problemi çözmemizi engelleyecektir. Öncelikle bu kaba çözüme bir bakalım, ardından kodumuzu nasıl hızlandırabileceğimizi düşünelim.

Sonuç: 233168 olarak bulunur.

Mantıksal Yaklaşım

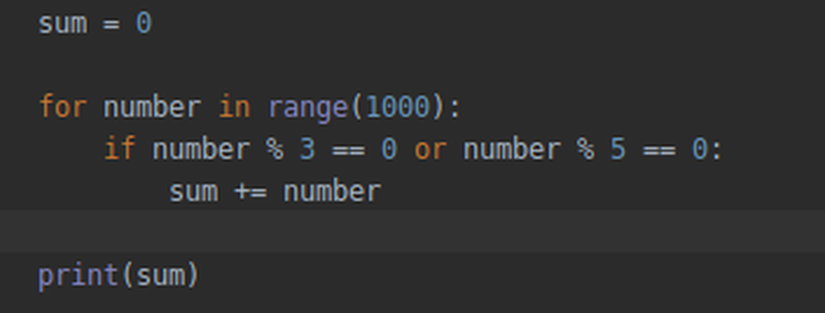
Aslında soruda bize verilen “3 veya 5″ ifadesi bir mantık operatörü içeriyor. C#’da veya operatörü || ile gösterilir. Bunu kodumuz içerisinde kullanarak biraz daha basit bir ifade elde edebiliriz.

C# Çözümü

Python Çözümü

Matematiksel Yaklaşım

Buradaki sorulara matematiksel çözümler getirmemiz işimizi oldukça kolaylaştırıyor. Hatta bir noktadan sonra soruların zorluğu, matematiksel yöntemler kullanmayı zorunlu kılıyor. Bu sorumuzda toplamlar söz konusu olduğu için basit toplam yöntemlerini inceleyerek kağıt kalemle dahi birkaç dakikada cevabı bulmak mümkün. İsterseniz elle yapın, isterseniz metodu kullanarak programa yaptırın. Benim kağıt üzerinde hesaplayarak çözmem beş dakikamı ya aldı ya da almadı.

Kaba çözümde 1’den 1000’e kadar olan sayıları bir bir artırarak her seferinde 3 veya 5’e bölünüp bölünmediğine bakıyorduk. Oysa ki katların toplamı şeklinde ifade edebiliriz. N₁ 3 ve katlarının toplamı olmak üzere;

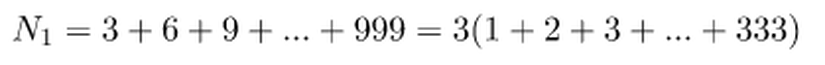
Aynı şekilde 5 için de

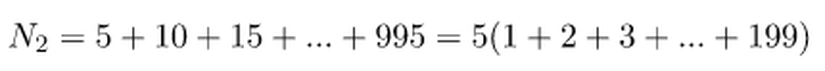
Ayrıca çıkarmak istediğimi 15’in katlarını da aynı şekilde bulabiliriz.

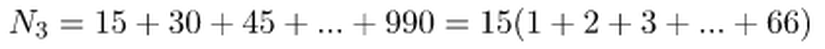
Gauss yöntemini uygulayarak ardışık sayı dizilerinin toplamlarını kolaylıkla bulabiliriz. N=1+2+3+…+n şeklinde verilen bir dizi için toplam;

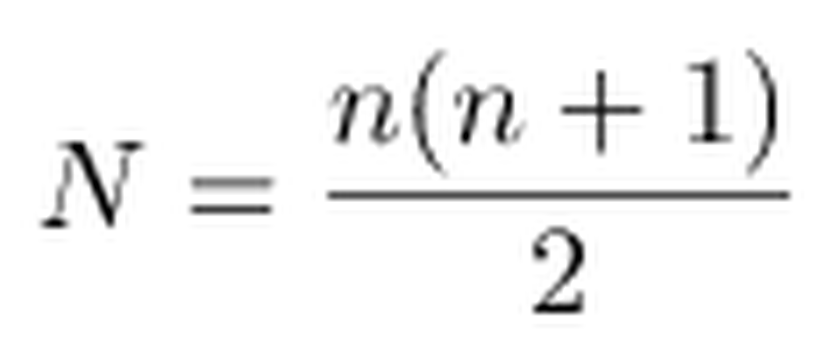
şeklinde ifade edilir. Bu durumda (1) + (2) – (3) işlemi bize sonucu vereceğinden cevap (4) no’lu ifade kullanılarak aşağıdaki gibi bulunur.

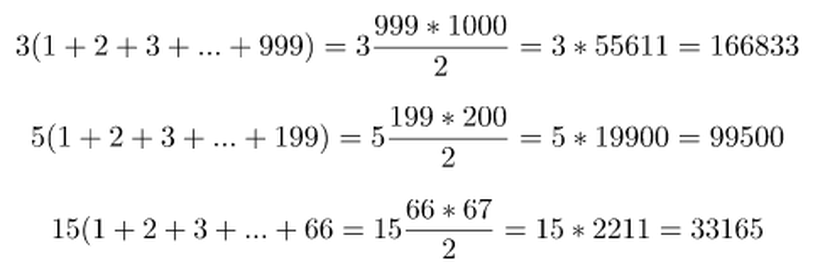
Böylelikle sonuç 166833 + 99500 – 33165 = 233168 olarak bulunur.

Ögetay Kayalı