Robertson-Walker Metriği Nedir? Pi Sayısı Hangi Koşullar Altında Sabittir?
 New Scientist
New Scientist
- Özgün
- Fiziksel Kozmoloji
Robertson-Walker metriği, kozmolojide evrenin homojen ve izotropik olduğu varsayımı altında sıklıkla kullandığımız bir metriktir. Yapısal olarak küresel kutupsal koordinatlara oldukça benzer, fakat evrenin geometrisine dair bazı ekler barındırır.
Koordinatlar
Gündelik yaşantımızda, iki nesne arasındaki uzaklığı tanımlamak oldukça kolaydır. En basitinden bir koordinat sistemi yardımıyla uzaklık tanımlayabiliriz. Kartezyen, yani (x,y,z)(x,y,z) koordinat sistemi üzerinde iki parçacığı yerleştirdiğimizi düşünelim. Bu iki parçacığın (x,y,z)(x,y,z) koordinatları arasındaki uzaklık farkları (dx,dy,dz)(dx,dy,dz) ise, bu durumda aralarındaki mesafe dsds'yi aşağıdaki şekilde ifade ederiz:
ds2=dx2+dy2+dz2\Large ds^2 = dx^2+dy^2+dz^2
Bu tanımlama çok sıradan bir tanımlamadır ve kartezyen koordinatlarda çalışmak, her ne kadar basit gibi görünse de aslında oldukça yorucudur. Bunun yerine küresel kutupsal koordinatlar üzerinden hareket etmek çok daha pratiktir. Parçacığın orijinden uzaklığı rr, yy ekseni ile yaptığı açı ϕ\phi ve z ekseni ile yaptığı açı θ\thetaolsun. Böylelikle iki parçacık arasındaki uzaklık, bir uzunluk birimi ve iki açı cinsinden kolaylıkla ifade edilebilir. Bu durumda benzeri bir yaklaşımla, iki parçacık arasındaki mesafeyi aşağıdaki şekilde ifade edebiliriz.
ds2=dr2+r2dθ2+r2sin2(θ)dϕ2\Large ds^2=dr^2+r^2d\theta^2+r^2sin^2(\theta)d\phi^2
Buraya kadar her şey oldukça güzel. Böylelikle herhangi bir noktadaki iki parçacık arasındaki mesafeyi rahatlıkla ölçebiliriz öyle değil mi? Aslında hayır. Çünkü tüm bunlar, düz bir uzay üzerinde geçerlidir. Fakat evren için bir geometriden bahsetmek durumundayız. Yani bir noktadan diğerine dümdüz gittiğinizi sansanız da aslında dümdüz gitmiyor olabilirsiniz. Tıpkı Dünya üzerinde hareket etmek gibi... Eğer yeterince ilerlerseniz, başladığınız noktaya geri dönersiniz, çünkü Dünya küresel bir geometriye sahiptir. Bu yüzden, evren için işin içerisine geometrisini de dahil eden bazı parametreler eklemeliyiz.
Robertson-Walker Metriği
Evrenin izotropik ve homojen olduğu varsayımı altında, olası tek bir metrik söz konusudur. Elbette küçük ölçeklerde farklı konuşulabilir, fakat büyük ölçekte dikkate almamız gereken bazı şeyler vardır. Bu metrik, yani Robertson-Walker metriği, aslında küresel kutupsal koordinatların biraz değiştirilmiş halidir.
ds2=a(t)2(dr21−kr2+r2dθ2+r2sin2(θ)dϕ2)\Large ds^2=a(t)^2(\frac{dr^2}{1-kr^2}+r^2d\theta^2+r^2sin^2(\theta)d\phi^2)
Burada a(t)a(t) basitçe; evrenin kendi üzerine çöküp çökmeyeceğini ya da tüm evrenin genişleyip genişlemeyeceğini ifade eden ölçek faktörüdür. kk ise, evrenin geometrisini ifade eder.
Bir an için a(t)a(t)'nin sabit olduğunu düşünüp, kk'nın, iki parçacık arasındaki mesafe için durumu nasıl değiştireceğini ele alalım. Çünkü a(t)a(t) zamanın bir fonksiyonudur ve aynı anlarda değeri aynıdır. Bu yüzden, geometriyi değerlendirmek adına onu görmezden gelebiliriz.
Eğer k=0k=0 olursa, bu durumda ilk terim dr2dr^2 olacak ve denklemimiz a(t)2a(t)^2 ifadesi hariç, küresel kutupsal koordinatlardaki formuna dönecektir. Böylesi bir durumun düz evren için geçerli olduğuna dikkat edin. Zaten az önce de yukarıda bahsettiğimiz formülasyonun, düz bir uzayda geçerli olacağını söylemiştik. Yani küresel kutupsal koordinatlarda yaptığımız mesafe ölçümü, herhangi bir eğriliği barındırmıyordu. Bu yüzden k=0k=0 için, küresel kutupsal koordinatlardaki formun aynısına ulaştık. Yani k=0k=0 için, düz bir evren söz konusudur. k<0k<0 ve k>0k>0 için durum biraz daha farklıdır ve bu durum, π\pi sayısının sabit olmamasına neden olmaktadır! Yani π\pi sayısı, yalnızca düz bir evrende sabit bir sayıdır.
Geometriye Göre π\pi Sayısının Değişimi
Tekrar a(t)2a(t)^2 terimini göz ardı edelim. Çünkü bu fonksiyon zamanın bir fonksiyonudur, dolayısıyla aynı zamanlar için aynı değeri alacağından kk'nın değişimini incelemek için bunu göz ardı edebiliriz. Bu durumda Robertson-Walker metriği, küresel kutupsal koordinatlara çok benzemektedir. Bir tek fark vardır, o da ilk terimde paydada bulunan 1−kr21-kr^2'dir. Dikkat ederseniz, denklemin açısal kısımları tamamen aynıdır.
Eğer k>0k>0 ise, bu durumda 1−kr21-kr^2 küçük bir değer alır ve bundan dolayı ds2ds^2 büyük bir değer alır. Yani böyle bir geometri üzerinde bir çember alırsanız, çevresi düz bir geometrideki çemberle tamamen aynı olacaktır, fakat rr değişecektir. Çevre aynı kalır, çünkü denklemin açısal kısımları değişmemekte, yalnızca uzaklık birimi (rr) değişmektedir. Burada rr büyük bir değer aldığına göre, çevrenin aynı kalması için π\pi daha küçük bir değer almalıdır.
k<0k<0 durumunda ise, tam aksi bir durum gerçekleşir ve π\pi daha büyük değerler alır. Oldukça garip bu durumun, gerçekten büyük ölçeklerde gerçekleştiğine dikkat edin.
Belirtmek gerekir ki bu durum elbette bir kabule dayanmaktadır. Bunu fiziksel bir gerçeklik değil, geometrinin ne kadar ilginç yorumlamalara neden olabileceğini göstermeye çalışan bir metafor olarak görmelisiniz.
Detaylı Çözüm
Bir çember üzerinde dθd\theta kadar bir birim alalım. Bu durumda rr sabit olduğu için dr=0dr=0 olur, aynı zamanda ϕ\phi de sabit olacağından dϕ=0d\phi=0 elde ederiz. Bu durumda elimizdeki metrik şöyle olacaktır:
ds2=a(t)2r2dθ2\Large ds^2=a(t)^2r^2d\theta^2
Terimlerin kareleri üzerinden bir sadeleştirme yapacak olursak şu eşitliği elde ederiz:
ds=a(t)r0dθ\Large ds=a(t)r_0d\theta
Buradaki rr değeri için r0r_0 diyelim ve bu bizim referans değerimiz olsun. Çemberin çevresi için cc dersek, birim açı elemanının tüm çember boyunca integrallenmesi ile cc değerini bulabiliriz:
c=∫02πa(t)r0dθ\Large c=\displaystyle\int_0 ^{2\pi} a(t)r_0d\theta
Böylelikle çemberin çevresi, şu şekilde bulunur:
c=2πr0a(t)\Large c = 2\pi r_0 a(t)
Şimdi de aynı şeyi, yarıçap boyunca ilerleyerek birim uzaklık elemanı drdr üzerinden yapalım. Çemberin çapı dd, çemberin çevresi cc ve π\pi cinsinden d=c/πd=c/\pi olarak ifade edilir. Eğer Robertson-Walker metriğine tekrar geri dönersek, birim açı elemanları sıfır olacağından, sadece ilk terim kalır. Bu durumda dd, şöyle ifade edilir:
d=2∫0r0a(t)dr(1−kr2)\Large d= 2\displaystyle\int_0^{r_0} \frac{a(t)dr}{ \sqrt{(1-kr^2)}}
Bu integralin çözümünden k<0k<0 için arcsinharcsinh, k>0k>0 için arcsinarcsin'e bağlı bir ifade gelir.
Eğer k>0k>0 ise denklem şu hale gelir:
π=π0rkarcsin(rk)\Large \pi = \pi_0 \frac{r \sqrt{k}}{arcsin(r \sqrt{k})}
Eğerk<0 k<0 ise, denklem aşağıdaki şekildedir. Denklemin çözüm koşulu da budur, aşağıdaki denklemde kk için pozitif değerlerin kullanılması gerekir.
π=π0rkarcsinh(rk)\Large \pi = \pi_0 \frac{r \sqrt{k}}{arcsinh(r \sqrt{k})}
Sonuç
Bu durumda π\pi sayısı, yalnızca düz bir evren (k=0k=0) için, sabit bir sayıdır. k<0k<0 ve k>0k>0 için π\pi, rr'ye bağlı olarak açıkladığımız gibi bir değişim gösterecektir. k>0k>0 için giderek küçülecek, k<0k<0 için ise giderek büyüyecektir. Neden büyük ölçeklerin ele alındığını da böylece görmüş olduk. Çünkü rr'nin küçük değerleri için fark çok az olmaktadır.
Bu duruma yol açan temel etmenin, metrikteki kr2kr^2 ifadesinden geldiğine dikkat edin. k=0k=0 olduğu durumda rr'ye bağımlılık yok olur. Dolayısıyla rr değişse de π\pi değişmez. Fakat kk'nın farklı değerlerinde rr'ye bağlılık vardır ve bu bağlılık, kk'nın aldığı değerlere göre aşağıdaki gibi bir grafik verir.
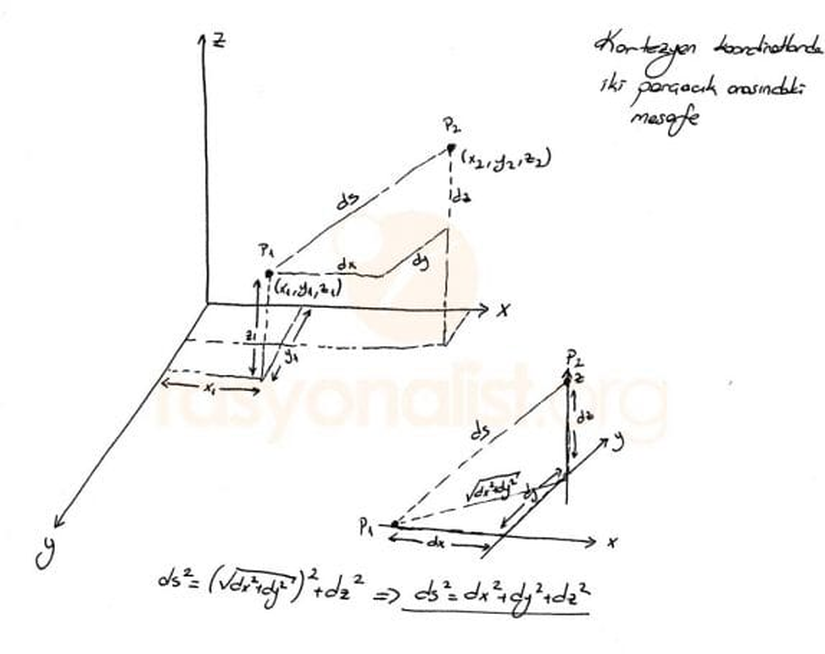
Yukarıdaki grafikte, her üç eksenin birbirine dik olduğuna dikkat edin. Bu sayede Pisagor eşitliğini kullanabildik. Belirtmek gerekir ki açılar, bakış doğrultumuzdan ötürü 90 derece değil gibi görünse de gerçekte bu üç doğru (x,y,z)(x,y,z) birbirine diktir.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 3
- 2
- 1
- 1
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- P. Francis, et al. Astrophysics Xseries Program. Alındığı Tarih: 29 Aralık 2023. Alındığı Yer: edX | Arşiv Bağlantısı
- P. P. Coles. (2003). Cosmology. ISBN: 9780470852996. Yayınevi: John Wiley & Sons.
- Ohio State University. (Ders Notu). A682: Introduction To Cosmology Course Notes.
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 20/04/2024 11:07:41 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12738
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.



