Evrenin Yoğunluğu Ne Kadardır ve Nasıl Hesaplanır?

- Özgün
- Fiziksel Kozmoloji
Evrenin geometrisini belirleyen parametre, evrenin yoğunluğudur. Eğer evrenin yoğunluğu, kritik yoğunluk değerinden fazlaysa evrenin geometrisi kapalı bir geometri; kritik yoğunluktan azsa açık bir geometridir. Tam olarak kritik yoğunluğa eşit miktarda yoğunluk olması durumundaysa evrenin geometrisi düz olacaktır. Peki evrenin yoğunluğu nasıl ölçülür?

Evrenin belirli bir bölgesini alıp tartıya koyma imkânımız olmasa da belirli yöntemler sayesinde bu bölgenin kütlesini tahmin edebiliriz. Sonra bu yöntemi her bölgeye uygulayarak toplam yoğunluğu bulmaya çalışırız. Fakat bu pek de pratik bir yöntem değildir. Çünkü öncelikle bir şeyin kütlesini ölçebilmek için, o nesneyi görebilmeniz gerekir.
Bir galaksinin kütlesini, onun parlaklığından yola çıkarak tahmin edebilirsiniz. Çünkü galaksinin parlamasına sebep olan şey, içerisinde bulunan yıldızlardır ve bunların kütleleri aşağı yukarı tahmin edilebilir. Fakat yıldızlararası ortamda bulunan madde ve intergalaktik ortamda bulunan maddenin kütlesini hesaplamak bu kadar kolay değildir.
Üstüne üstlük, gördüğümüz bu maddenin aslında bir bütünün çok ufak bir parçası olduğu gözlemlerle gösterilmiştir. Bunun yanında bir de hiçbir şekilde gözleyemediğimiz, fakat etkileri sayesinde dolaylı olarak farkında olduğumuz karanlık madde bulunur. Bu da yetmez, evrende bir de karanlık enerji vardır. Bugün mevcut olan teorik bilgimiz ile elde ettiğimiz gözlem sonuçları bize, evrenin yalnızca %4.9'unun bildiğimiz, baryonik maddeden oluştuğunu gösteriyor. %26'lık kısım karanlık maddeye aitken, %69.1'lik kısım da karanlık enerjiden oluşuyor.
Bu ölçümler ise, kozmik mikrodalga arka plan ışıması (CMBR) olarak bildiğimiz, evrenin yaklaşık 400.000 yıllık yaşından arta kalan ışınımından elde ettiğimiz veriler sayesinde yapılıyor. Çok detaylı analizlerin kuvvet tayfı sayesinde incelenmesiyle yoğunluk dağılımları belirlenebiliyor. Tayfın biçimi, yoğunluk parametrelerinin dağılımı hakkında doğrudan bilgi veriyor; böylece maddeyi doğrudan gözlemlemeden sadece bildiğimiz davranışını yorumlayarak evren üzerindeki etkisinden dağılımının ne olduğunu bilebiliyoruz.
Evrenin belirlenmiş yoğunluk değeri 8.64 x 10-27 kg m-3'dür. Bu oldukça küçük bir değer gibi görünebilir; fakat bu birimler galaksi kütlesine ve intergalaktik mesafeye çıkarıldığında, sonucun oldukça normal olduğu görülür. Bu değer aynı zamanda kritik yoğunluğa da yaklaşık olarak eşittir, bu da aşağıda tanımlanan yoğunluk parametresinin 1'e yaklaşık olarak eşit olduğunu gösterir.
Hesaplamalar
Yoğunluk parametresi (Ω\Omega), toplam yoğunluğun kritik yoğunluğa oranı olarak şöyle tanımlanır:
Ω(t)=ρρc\Large{\Omega(t) = \frac{\rho}{\rho_c}}
Burada kritik yoğunluk, Friedmann denklemlerinden k=0k=0 (düz bir evren) için elde edilen yoğunluk değeridir ve aşağıdaki değere sahiptir:
ρc(t)=3H28πG\Large\rho_c(t)=\frac{3H^2}{8\pi G}
ρc(tc)=1.88h2×10−26 kg m−3\Large\rho_c(t_c)=1.88h^2\times{10^{-26}}\space kg\space m^{-3}
Genellikle Hubble sabiti yerine, birimsiz hh değeri kullanılır. Yukarıdaki hh ifadesi, aşağıdaki şekilde tanımlanır:
h=H0100 km s−1 Mpc−1\Large h = \frac{H_0}{100\space km\space s^{-1}\space Mpc^{-1}}
Yoğunluk parametresi (Ω\Omega), bileşenleri cinsinden aşağıdaki şekilde ifade edilebilir. Bunu farklı kaynaklarda farklı şekilde görebilirsiniz. Genellikle bileşenler baryonik madde, karanlık madde ve karanlık enerji olarak üçe ayrılır. Fakat bazen relativistik madde, relativistik olmayan madde gibi sınıflandırmalar da yapılabilir.
Ω=Ωb+Ωkm+ΩΛ\Large\Omega = \Omega_b + \Omega_{km} + \Omega_{\Lambda}
Burada toplam yoğunluğun 1 olması gerekmediğine dikkat edin. Yoğunluk parametresi, toplam yoğunluğun kritik yoğunluğa oranı olduğundan herhangi bir değeri alabilir. Fakat düz bir evren için bu değer 1'dir. Bu yüzden bizim sonuçlarımızda Ω\Omega, 1 olarak gösterilir.
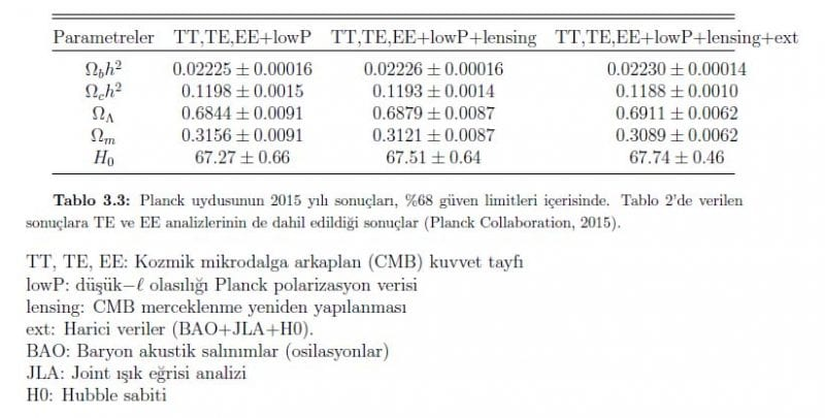
Yukarıdaki tabloda, yoğunluk parametrelerinin 2015 yılı için değerlerini görebilirsiniz.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 3
- 2
- 2
- 1
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- P. Coles. Cosmology: The Origin And Evolution Of Cosmic Structure. ISBN: 9780471954736.
- A. Liddle. (2015). An Introduction To Modern Cosmology. ISBN: 9781118502143. Yayınevi: John Wiley & Sons.
- P. Collaboration, et al. (2015). Planck 2015 Results. Xiii. Cosmological Parameters. EDP Sciences, sf: A13. doi: 10.1051/0004-6361/201525830. | Arşiv Bağlantısı
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 19/04/2024 20:54:48 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12949
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.



