Kütleçekimsel Merceklenme Nedir? Galaksilerden Gelen Işık Bize Ulaşmadan Önce Nasıl Kırılıyor?
 NewsBeezer
NewsBeezer
- Özgün
- Fiziksel Kozmoloji
Einstein 1915 yılında Genel Görelilik Teorisini ortaya attığında; maddenin uzay-zamanı büktüğünü ve aynı zamanda maddenin bu bükülmüş uzay-zamanda hareket etmesi gerektiğini biliyordu. Yani cisimler, ortamın geometrisini takip etmek zorundaydı. Bu da kütleçekimsel bir alandan geçmekte olan ışığın rotasının değişmesi gerektiğini ima eder. Bu durum, kütle çekimsel merceklenmenin temelini oluşturur.

Her cisim, kütlesinden ötürü ışığın rotasını bir miktar saptırabilir. Fakat burada basit bir sapınçtan bahsetmiyoruz. Burada öylesine bir sapınç var ki artık uzay-zamanın kendisi ciddi bir biçimde bükülmüş olduğundan tıpkı bir mercek gibi görev görüyor. Arka planında kalan cisimlerin görüntülerini bozuyor, onları büyütüyor ve hatta görüntülerini çoğaltıyor.
Yukarıdaki APOD görselinde 4 milyar ışık yılı uzaklıkta yer alan çok büyük kütleli Abell 370 galaksi kümesinin sebep olduğu çekimsel merceklenme görülüyor. Galaksi kümesi uzay-zamanı öylesine büküyor ki, arka planda kalan galaksilerin görüntüsü bozuluyor. Kümenin etrafında çeşitli ark (yay) şeklinde galaksiler görmeniz de bundan kaynaklanıyor. Ön planda kalanlar ise durumdan etkilenmiyor.
Galaksi kümesinin kütlesi, parlaklığından yola çıkarak belirlenebilir. Fakat bu şekilde bir kütle ölçümü yapacak olursanız, böylesi bir merceklenme olayı hakkında yanlış sonuçlara varırsınız. Çünkü parlaklıktan yola çıkarak yapılan ölçüm, ışıma yapan maddenin kütlesini verir. Oysa ki geçmiş gözlemlerden biliyoruz ki, kümedeki toplam maddenin önemli bir miktarını görünmeyen karanlık madde oluşturuyor. Bu sayede kütleçekimsel merceklenme etkisini kullanarak, kümedeki karanlık madde miktarı hakkında çıkarımlar yapmak da mümkün oluyor.
Kütle çekimsel merceklenme, görüntü bakımından bazı özel durumları doğurabiliyor. Eğer arka planda yer alan cisim, merceklenmeyi yapan ile aynı doğrultuda hizalanmış ise cismin görüntüsü, merceklenmeyi yapanın etrafında bir halka oluşturuyor.
Bir diğer örnek ise "Einstein haçı" olarak adlandırılıyor.[1] Galaksilerin disk şeklindeki yapılarından ötürü, bir önceki örnekte bükülerek bir ark (yay) oluşturuyorlardı. Fakat söz konusu cisim kuazar gibi bir nokta kaynak olduğunda, bir yay yerine aynı kuazarın kopyalanmış birkaç görüntüsü oluşuyor.
Kütleçekimsel Merceklenme Türleri ve Hesaplamalar
Kütleçekimsel merceklenmeye sebep olan durumlar, çeşitli koşullar altında oluşabilir. Eğer Einstein halkası, arklar, bozulmalar ve çoklu görüntüler oluşuyorsa burada güçlü bir merceklenme kaynağı olduğundan dolayı bu olaya güçlü merceklenme denir.[2] Eğer görüntüde çok bariz bir değişim yoksa, çekimsel merceklenme çok zayıfsa ve yalnızca çok sayıda örnek istatistiksel yolla incelenerek bir etki bulunuyorsa, buna zayıf merceklenme denir. Eğer görüntüde herhangi bir bozulma yoksa, fakat cismin parlaklığını artırabiliyorsa buna da mikromerceklenme denir.
Hesaplamalar
Lensin, yani merceğin yarattığı kırılmayı göstermek için aşağıdaki resmi kullanalım. Bu resimdeki açılar ve mesafelerle bazı hesaplamalar yapabiliriz.
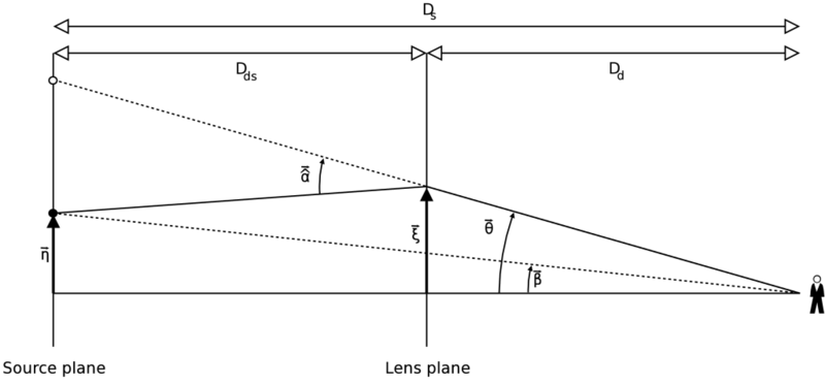
İlk olarak, resimde bulunan küçük açıları kullanarak aşağıdaki eşitlik yazılabilir:
θDs=βDs−α^Ds\Large \theta D_s = \beta D_s - \hat{\alpha}D_s
Buradan elde edilen aşağıdaki denklem, lens denklemi olarak adlandırılır:
β=θ−α(θ)\Large \beta = \theta - \alpha (\theta)
Bu denklem, görüntünün açısal konumu ile kaynak arasında bir ilişki tanımlar. Aşağıdaki gibi bir DD tanımlaması yapalım:
D=DdDsDds\Large D = \frac{D_d D_s}{D_{ds}}
Keyfi bir kütle profiline sahip çembersel bir lens durumunu genelleyecek olursak şöyle yazılabilir:
β=θ−DdsDdDs4GM(θ)c2θ\Large\beta = \theta - \frac{D_{ds}}{D_d D_s} \frac{4GM(\theta)}{c^2\theta}
Eğer kütle yoğunluğu yeterliyse, beta sıfır için optik eksen boyunca yer alması durumunda bir "Einstein halkası" oluşturur. Bu halkanın yarıçapının karesi aşağıdaki şekilde ifade edilir:
θE2=4GM(θE)Dc2\Large\theta _E^2 = \frac{4GM(\theta_E)}{Dc^2}
Böylece nokta kaynak için aşağıdaki eşitliği elde ederiz:
θE=(4GMDc2)1/2\Large\theta _E = (\frac{4GM}{Dc^2})^{1/2}
Bunu lens denklemini yeniden yazmak için kullanırsak lens denklemi şu hale gelir:
β=θ−θE2θ\Large \beta = \theta - \frac{\theta_E^2}{\theta}
Bunun iki çözümü bulunur:
θ±=12(β±β2+4θE2)\Large \theta _\pm = \frac{1}{2} (\beta \pm \sqrt{\beta^2 + 4\theta_E^2})
İki çözüm, iki görüntüye karşılık gelir, biri kaynağın diğer tarafında yer alır. Görüntünün biri daima Einstein halkasının içerisinde yer alırken diğeri dışındadır. Eğer kaynak optik eksenden uzaklaştırılırsa (β\beta artarsa), görüntünün biri lense yakınlaşırken diğeri de kaynağa yakınlaşır. Çekimsel merceklenme aynı zamanda kaynağın görünür katı açısını da değiştirir. Bu durum cismin boyutunun büyütülmesi anlamına gelir. Görüntü alanının, kaynak alanına olan oranı kadar bir büyütme olur ve çembersel bir lens için bu çarpan aşağıdaki şekilde ifade edilebilir:
μ=θβdθdβ\Large \mu = \frac{\theta}{\beta} \frac{d\theta}{d\beta}
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 1
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- ^ R. Nave. Einstein Cross. Alındığı Tarih: 29 Şubat 2024. Alındığı Yer: HyperPhysics Concepts - Georgia State University | Arşiv Bağlantısı
- ^ R. Nave. Einstein Ring. Alındığı Tarih: 29 Şubat 2024. Alındığı Yer: HyperPhysics Concepts - Georgia State University | Arşiv Bağlantısı
- P. Coles. Cosmology: The Origin And Evolution Of Cosmic Structure. ISBN: 9780470852996.
- K. Yakut. (Ders Notu). Ege Üniversitesi Astronomi Ve Uzay Bilimleri, Extragalactic Astronomy Ders Notu.
- J. D. Cohn. Gravitational Lensing. Alındığı Tarih: 29 Şubat 2024. Alındığı Yer: University Of California Department of Astronomy | Arşiv Bağlantısı
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 24/04/2024 17:19:33 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12741
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.



