Fraktallar: Göz Kamaştıran Geometrik Şekiller!
Julia ve Mandelbrot Kümeleri Nedir? Koch Kar Tanesi Nasıl Görünür?
 Wikipedia
Wikipedia
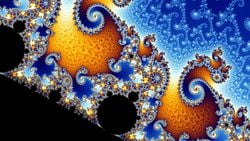
Fraktallar, büyükten küçüğe birbirine benzeyen birçok geometrik şeklin oluşturduğu, sonsuzluğa doğru giden, kompleks ve göz kamaştırıcı şekillerdir. Fraktal kelimesi Latince’deki ‘’fractus’’ kelimesinden türetilmiştir, kırılmış ve parçalanmış anlamına gelmektedir. Fraktal, bir geometri sistemidir; fraktallar yakından incelendiğinde büyük şekli oluşturan ve orantılı olarak küçülerek oluşan küçük şekillerin büyük şekle benzediği ve bu kendini tekrar etme olayının sonsuzluğa uzandığı görülür.
Fraktallarla İlgili İlk Çalışmalar
Fraktal şekillerle ilgili ilk çalışmalar Fransız matematikçiler Gaston Julia (1893-1978) ve Pierre Fatou (1878-1929) tarafından yapılmıştır fakat onların yaşadığı zaman diliminde bilgisayarlar henüz bu fraktalları gösterebilecek kadar gelişmediğinden, Gaston Julia kendi oluşturduğu fraktal kümesinin (Julia kümesi) şeklini bilgisayarda görememiştir.
Fraktal terimi ilk defa Polonya asıllı matematikçi Benoit Mandelbrot (1924-2010) tarafından 1975 yılında ortaya atılmıştır. Mandelbrot’un geliştirdiği Mandelbrot kümesi, sanal karmaşık sayıların kullanılmasıyla elde edilen fonksiyonları bilgisayar ortamında muhteşem fraktallara dönüştürülebilen kümedir.


Doğadaki Fraktal Örnekleri
Mandelbrot’un öncülüğünü yaptığı, bilgisayar ortamında ortaya çıkan muhteşem fraktal örneklerini incelemeden önce doğadaki fraktal örneklerine bir bakalım. Doğadaki fraktallar karmaşık ve düzensizdir. Daha önce hiç fraktal örneği görmemiş olsanız bile fraktal tanımına uygun örnekleri hemen bulabilirsiniz. Örneğin brokoli , karnabahar, kar tanesi veya eğrelti otunda gördüğümüz şekiller fraktal örnekleridir.
Bu şekillere baktığımızda ne kadar estetik olduklarını düşünürüz. Mandelbrot’a fraktalın ne olduğu sorulduğunda ağaç örneğini vermiştir. Ağacın dallarının ağacın kendisine benzediğini ve dallandıkça kendine benzeyen küçük ağaçcıklara dönüştüğünü anlatır Mandelbrot. Buradan fraktalın ortaya çıkışının doğadan esinlenerek gerçekleştiği düşünülebilir. Tabii ki, daha önce söylediğimiz gibi doğadaki fraktal örnekleri bilgisayarda şekillendirilen fraktal örnekleri kadar mükemmel değildir. Doğadaki birbirini tekrarlamalar birbirine çok benzese de, birbirinin aynısı olamaz.


Julia ve Mandelbrot Kümesi
Gelelim bilgisayar ortamında oluşturulan fraktallara. Yazının başında da söylediğimiz gibi Fransız matematikçi Gaston Julia ilk olarak fraktal geometrisi ile uğraşan kişilerden biridir ama oluşturduğu Julia kümesinin şeklini görme şansı olmamıştır.

Fraktal terimi ise Benoit Mandelbrot tarafından 1975 yılında ortaya atılmıştır. Mandelbrot kümesinin fraktal şekli, 1979 yılında IBM bilgisayarlarına erişince oluşturulabilmiştir. Mandelbrot kümesi, bir dizi karmaşık sayının oluşturduğu fraktal şekildir. Mandelbrot, bu kümenin oluşumuna dair formülü kullanarak birbirinin benzeri şekillerin küçülerek sonsuza kadar oluştuğunu gözlemiştir.
Bu şekiller renklendirildiğinde görsel olarak büyüleyici şekiller oluşur. Bilgisayar ortamında oluşturulan Mandelbrot kümesi son derece basit bir denklemden üretilir. Karmaşık sayılar düzleminde f(z)f(z) olarak tanımlanan fonksiyonda zz’nin karesi alınıp bir sabitin eklenmesiyle oluşur. Mandelbrot kümesi, z=z2+cz = z^2 + c denklemiyle gösterilir. Bu denklemde cc ve zz karmaşık sayılardır.
Mandelbrot Kümesinin Oluşturduğu Göz Kamaştıran Şekillerden Bazıları
Şimdi sırasıyla yayınlayacağımız şekiller, Mandelbrot kümesinin oluşturduğu başlangıç şekli üst üste büyütülerek elde edilmiştir. Mandelbrot bu çalışması sayesinde sanat ve bilim çevrelerinin hayranlığını kazanmıştır.


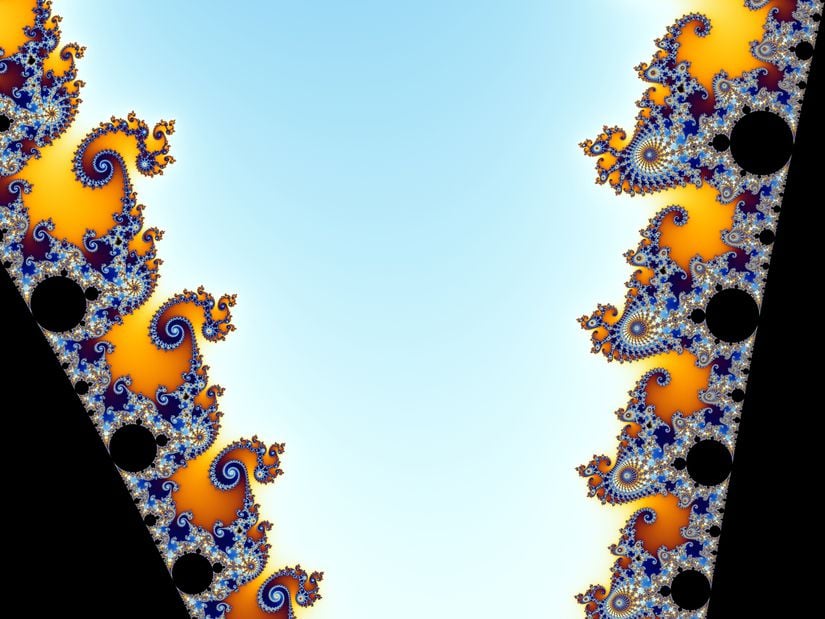





Gördüğünüz gibi ne kadar odaklanırsak o kadar ayrıntılı şekillere ulaşırız. Bu şekiller birbirini takip eden şekillerdir. Karşımıza Mandelbrot kümesinin başlangıcında yer alan siyah şekiller, denizatı vadileri, denizatları ve denizatlarının kuyrukları çıkar. Ortaya çıkan bu karmaşık şekiller adeta görsel bir şölen gibidir. Mandelbrot bir söyleşisinde şunları söylemiştir:
Bizi şaşırtan şey, hem Julia kümesi hem de Mandelbrot kümesindeki girifliğin, nasıl desek, keyfi olmamasıydı ve neredeyse herkeste bu şekillerin harikulade güzel olduğu izlenimi uyanmıştı. Bu şekiller çok basit bir fonksiyonun, z2+c’nin ciddiye alınması ve görselleştirilmesiyle ortaya çıktı. İnsanlar ilk başta bunun tamamen dünya dışına ait bir şey olduğunu düşündüler ama sonra, çok kısa bir süre sonra geri gelip şöyle dediler: "Biliyor musunuz, bunlar bana bir şey hatırlatıyor. Bence bunlar doğal. Kâbus ya da rüya gibiler ama doğallar." Ve bu kombinasyon; yeni olmaları, çünkü onları daha önce hiç kimse görmemişti ama diğer yandan da çok bilindik olmaları, bana hâlâ olağanüstü şaşırtıcı geliyor.
Koch Kar Tanesi: Kendiniz de Fraktallar Çizebilirsiniz!
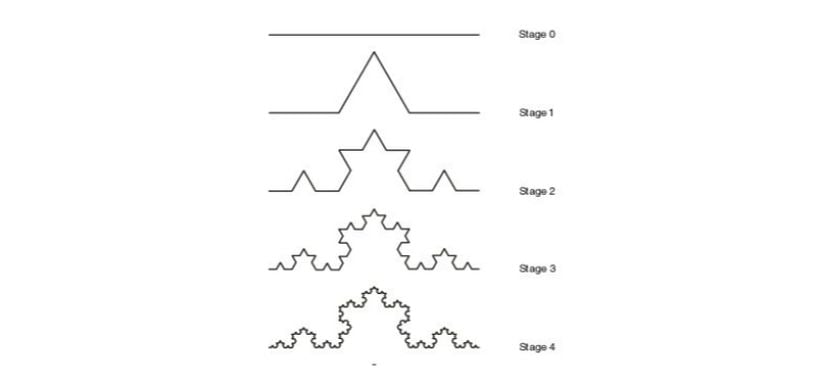
Basit bir eşkenar üçgen çizin. Sonra bunu üç parçaya bölerek ortadaki parçayı çıkarın. Ardından çıkardığınız yere, tabanıyla aynı uzunluğa sahip iki kenar daha çizerek bir üçgen daha oluşturun. Üç birim uzunluğa sahip bir kenarı, dört birim uzunluğa çıkarmış olacaksınız. Ardından bu süreci her kenar için tekrarlayarak devam edin. Tıpkı aşağıdaki gibi.
 Alvaro Costa
Alvaro CostaBu resimde gördüğünüz şekil bir fraktal olacaktır, eğer küçük üçgenlerden birine yakınlaşırsanız bir önceki sahnenin aynısını görürsünüz, çünkü siz de benzer bir üçgenle başlamıştınız.
Burada gerçekleşen olay, üç birim uzunluğundaki bir kenarı her seferinde dört birime çıkarmak. Dolayısıyla çevre her seferinde 4/3 kat artıyor. Bu da bu işlemi sonsuza kadar tekrarladığınızda, çevrenin sonsuza kadar artacağı ve ıraksayacağı anlamını taşıyor. Bir de bu şeklin alanını inceleyelim.
Eşkenar bir üçgenin alanını hesaplamak oldukça kolaydır, eğer bir kenarının uzunluğu aa birim ise, alanı 2a34\frac{2a\sqrt{3}}4'tür. İlk işlemde bu alana ek olarak üç eşkenar üçgen daha oluşur. Bu üçgenin kenarının biri a3\frac{a}3 birim uzunluğa sahiptir. İşlemde karesi alınarak gittiğinden, bir süre sonra yeni oluşup toplam alana eklenen üçgenlerin katkısı kaybolur. Detaylı bir hesap yapıldığında Koch kar tanesinin alanı 2(2a√3)5\frac{2(2a√3)}5 olarak bulunur. Yani şekil başlangıçtaki üçgenin alanının 85\frac{8}5 katı kadar bir alana sahiptir. Zaten şeklin ilerleyiş biçiminden, kar tanesinin belirli bir alan içerisine hapsolduğunu anlayabilirsiniz.
Öyleyse bu şeklin alanı sonlu, fakat çevresi sonsuzdur! Yani şeklin içini dolaşabilir, ama çevresini dolaşamazsınız! Ama bu nasıl olur? İçini dolaşırken kenarları da dolaşmış olmuyor muyuz? Demek ki sezgilerimizle örtüşmeyen bir durum söz konusu. Matematik oldukça basit olmasına rağmen, bu durumu anlamakta zorlanıyoruz. Bu da bizim, olası bilimsel çıkarımlarda dikkatli olmamız konusunda bize sağlam bir uyarıda bulunuyor. Bu yüzden bilimi, matematik gibi araçlar kullanarak geliştirmeye çalışıyoruz.
Eğer bunu anlamakta zorlanıyorsanız şöyle düşünün. Bir tane kare alın, bunun alanı bellidir, ölçebilirsiniz. Kenar uzunluğunu da hesaplayabilirsiniz. Şimdi bunu tam ortadan ikiye bölün, sonra kestiğiniz parçayı diğerinin yanına ekleyerek bir dikdörtgen elde edin. Alanınız değişmedi, çünkü yeni bir şekil eklemediniz. Fakat şeklinizin taban kenarının uzunluğu ikiye katlandı. Aynı işlemi tekrar yapın, taban uzunluğu tekrar ikiye katlanacak fakat alan hiç değişmeyecek. Bu işlemi sonsuz kez tekrarladığınızda, artık bir kareden bir doğru gibi incecik bir çizgi elde etmeye doğru ilerliyor olacaksınız. Uzunluğu sonsuz olacak, fakat alanı sonlu...
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 20
- 15
- 12
- 11
- 7
- 4
- 3
- 0
- 0
- 0
- 0
- 0
- Wikipedia, et al. Mandelbrot Set. (17 Aralık 2018). Alındığı Tarih: 17 Aralık 2018. Alındığı Yer: Wikipedia | Arşiv Bağlantısı
- Jack Challoner. How Mandelbrot's Fractals Changed The World. (18 Ocak 2010). Alındığı Tarih: 17 Aralık 2018. Alındığı Yer: BBC | Arşiv Bağlantısı
- Wikipedia, et al. Fractal. (17 Aralık 2018). Alındığı Tarih: 17 Aralık 2018. Alındığı Yer: Wikipedia | Arşiv Bağlantısı
- Wikiquote, et al. Benoît Mandelbrot. (17 Aralık 2018). Alındığı Tarih: 17 Aralık 2018. Alındığı Yer: Wikiquote | Arşiv Bağlantısı
- Simeon Hein. What Are The Fractals?. (18 Aralık 2018). Alındığı Tarih: 18 Aralık 2018. Alındığı Yer: Gaia | Arşiv Bağlantısı
- E. W. Weisstein. Koch Snowflake. Alındığı Tarih: 19 Mart 2024. Alındığı Yer: Wolfram Mathworld | Arşiv Bağlantısı
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 27/04/2024 05:41:46 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/7518
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.





