Kepler Yasaları Nedir? Kepler'in Gezegensel Hareket Yasaları Neyi Açıklar?

- Özgün
- Astronomi
Kepler yasaları, Kepler'in 17. yüzyılın başlarında ortaya attığı, gezegenlerin hareketini açıklayan üç ayrı kolda incelenen yasalardır. Bu yasalar, birlikte çalıştığı bilim insanı Tycho Brahe'den kalan verilerden yola çıkarak geliştirilmiştir ve hepsi oldukça temel gözlemsel verilere dayanmaktadır.
Tarihçe
Yasalara geçmeden önce, Kepler'in yaşadığı dönemin atmosferini ve onu bu devrim niteliğindeki başarıya götüren düşünceleri incelemek gerekiyor. Kepler'in yaptığı çalışmalar, yazının başında da dediğimiz gibi Tycho Brahe'nin uzun yıllar yaptığı gözlemlerin verilerine dayanıyordu. Tycho, Avrupa'nın en iyi üniversitelerinden birinde eğitim almış, daha sonra da kendi gözlem evinde (Uraniborg) yaptığı gözlemler sonucunda, Antik yunan görüşü olan Dünya merkezli evren modelinin doğru olmadığına ikna olmuş bir bilim insanıydı.
Tycho, yaşadığı bazı siyasi sorunlardan dolayı Prag'a taşınmak zorunda kaldı. Burası, Kepler ile tanışacağı ve onunla beraber çalışmalar yapacağı yerdi. Tycho'nun Kepler'e verdiği ilk görev, çembersel yörüngeye sahip olduğu düşünülen gezegenlerin konumlarının öngörülemezliğini çözmekti. Kepler ile bir yıl boyunca çalışan Tycho, bir yılın sonunda hayatını kaybetti. Ancak Tycho'nun yaptığı yüksek kalitedeki ve düşük hata payına sahip gözlemlerin verileri sayesinde Kepler, çok büyük başarılara imza atacaktı.
Kepler'in yapacağı bu çalışmalar onun tam 29 yılını aldı. Ancak Kepler, tüm bu çalışmanın sonucunda bir devrime imza attı ve gezegenlerin hareketini çok başarılı şekilde açıkladı. Ta ki yüzyıllar sonra Einstein gelip, eksikleri kapatana kadar.
Kepler Yasaları
Kepler yasaları, yörünge kinematikleri üzerine oldukça açıklayıcıydı. Birçok gök cisminin hareketini hala sorunsuz bir biçimde açıklayabilir. Fakat Merkür probleminden de biliyoruz ki, bazı durumlarda görelilik etkileri baskın hale geliyor ve Kepler yasaları kullanılamaz oluyor.
Kepler'in Birinci Yasası
Kepler'in Birinci Yasası şunu söyler: Her gezegen, odak noktalarından birinde Güneş’in bulunduğu eliptik yörüngelerde dolanır.
Kepler, Güneş merkezli evren modelini çok önceden kabul etmişti. Kopernik, bu modeli ortaya attığında, gezegenlerin çembersel yörüngelerde dolaştığını düşünmüştü. Ancak Kepler, Tycho'nun gözlem verileri sayesinde, bu düşünceyi terk etmişti.
Kepler yasalarının birincisini anlamak için, öncelikle elipsin geometrisini incelemek gerekiyor. Elips, basitçe basık bir çemberdir.
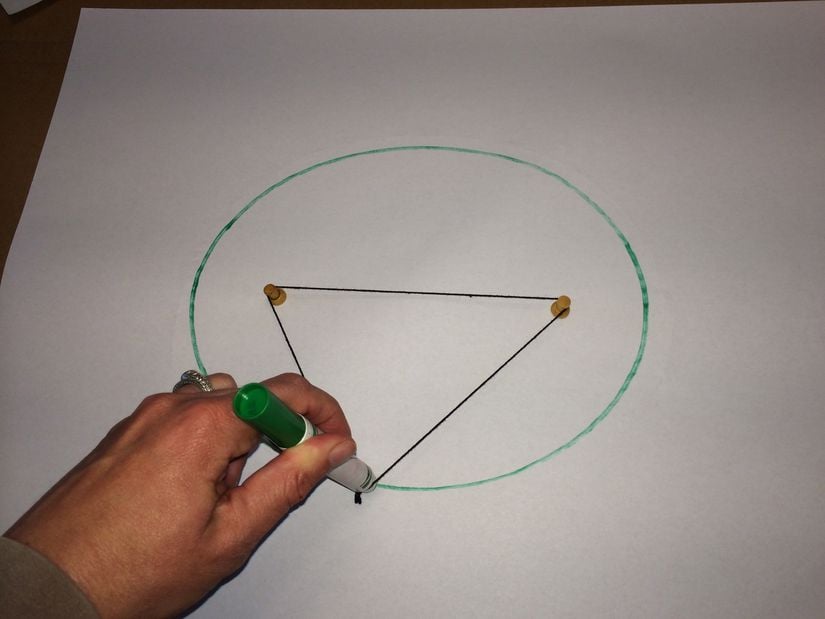
Modelde de gördüğümüz gibi, bir elipsi, iki toplu iğneyi bir kağıda sabitleyip ardından bu iğnelere bir ip bağlayarak çizebiliriz. Burada iki şey görebiliriz. Birincisi, toplu iğneler (odaklar) arası uzaklık arttıkça, elipsin basıklığı artar. İkincisi ise, toplam ipin uzunluğu hep eşit olduğundan, elips üzerindeki herhangi bir noktaya odaklardan çizilen iki doğrunun uzunluklarının toplamı her zaman eşit olmalıdır.
Kepler'in birinci yasasıyla bize söylediği şey budur. Gezegenler eliptik yörüngelerde gezer ve elipsin odaklarından birinde Güneş bulunur. Ancak, biz yine de diğer odağın neresi olduğunu bulabiliriz. Çünkü iki odak, merkeze göre simetriktir.
Kepler'in İkinci Yasası
Kepler'in İkinci Yasası şunu söyler: Güneş'ten herhangi bir gezegene çizilen doğru, eşit zamanlarda eşit alanlar tarar.
Kepler yasalarının ikincisini kolay şekilde anlamak için, bir model kullanabiliriz.
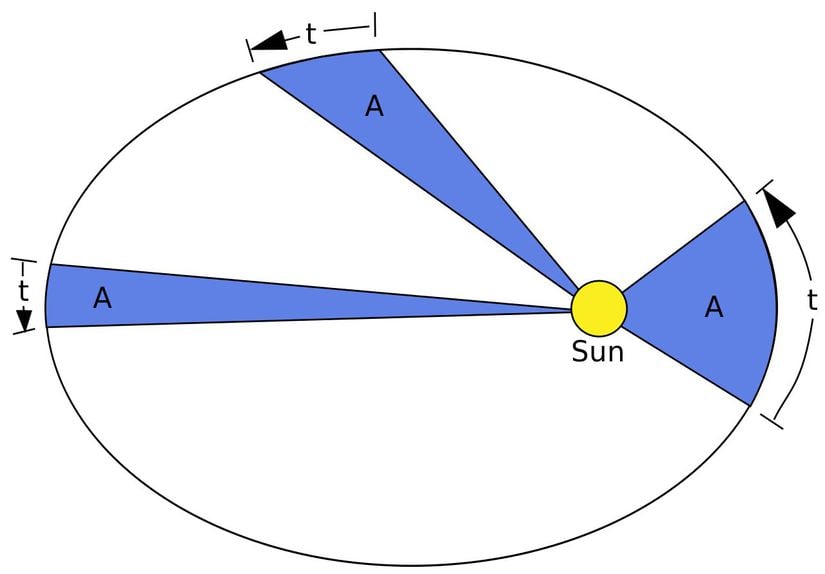
Yukarıdaki modelde Güneş etrafında dönen bir cismin eşit sürede kat ettiği mesafede taradığı alan her zaman eşittir. Tabii ki bunun sağlanabilmesi için, bu alan ne kadar ince-uzun ise (görselde solda taranan alanlar buna örnektir), gezegen de o kadar yavaş hareket eder. Taranan alan ne kadar şişman ve genişse (görselde sağdaki alan buna örnektir), gezegen de o kadar hızlı hareket eder. Yani gezegen, Güneş'e yaklaştıkça hızlanır, uzaklaştıkça yavaşlar. Bu bilgiden yola çıkan Kepler, "Gezegenler, yörüngelerinde eşit zamanda eşit alanlar tarar." yorumunu yapmıştır.
Kepler'in Üçüncü Yasası
Kepler'in Üçüncü Yasası şunu söyler: Gezegenin yörünge periyodunun karesi, elipsin yarı büyük eksen uzunluğunun kübüne eşittir.
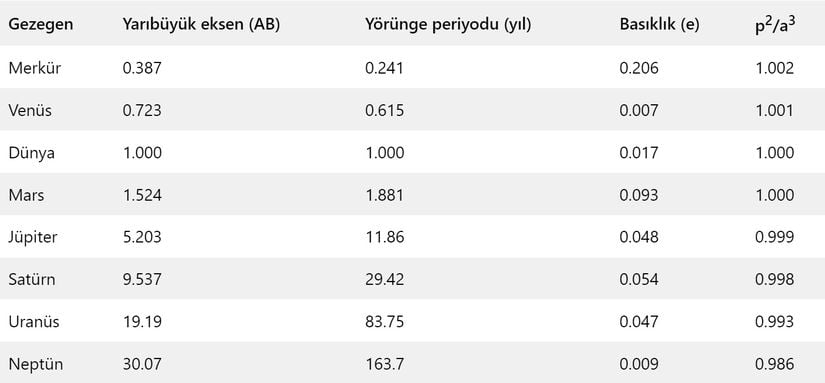
Yukarıdaki tabloda, gezegenlerin yarı büyük eksen uzunluğunu ve periyodunu görmekteyiz. En sağdaki sütunda da, P2 /a3P^2 / a^3 oranını görebiliriz. Tablodan da anlaşılabileceği gibi, sonuçlar birbirine çok yakın olsa da aynı değildir. Bunun sebebi ise, formülün gerçek halinin aşağıdaki gibi bir f(x)f(x) değişkenine eşit olmasıdır. Bunun sebebine ise, "ek bilgiler" kısmında değineceğiz.
P2 /a3 =f(x)\Large P^2 / a^3 = f(x)
Kepler yasaları, içinde bulunduğu dönem açısından oldukça önemliydi çünkü bilinen evren modeli, gözlemleri yeterince iyi açıklamıyordu ve oldukça karışıktı. Kepler, ortaya attığı bu hem anlaması kolay olan hem de gezegenlerin hareketini oldukça başarılı şekilde açıklayan yasalarıyla, büyük bir devrime imza attı.
Kepler Yasaları Hakkında Ek Bilgiler
Kepler yasalarının üçüncüsünde gördüğümüz P2 / a3 oranı basitçe nasıl elde edilebilir?
İşleme, çekim kuvvetini merkezcil kuvvete eşitleyerek başlayacağız.
GMmr2=mv2r\Large G\frac{Mm}{r^2}=\frac{mv^2}{r}
Ardından, gerekli sadeleştirmeleri yaparak devam edelim.
GMr=v2\Large G\frac{M}{r}=v^2
Çizgisel hızı farklı bir şekilde ifade edelim. Burada aslında hızı basitçe, yol/zaman ifadesi olarak yazıyoruz.
v=2πrT\Large v=\frac{2\pi r}{T}
Yerine yazdığımızda, karşımıza aşağıdaki gibi bir ifade gelecek.
GMr=4π2r2T2\Large G\frac{M}{r}=\frac{4\pi^2 r^2}{T^2}
Gerekli düzenlemeleri yaptığımızda, Kepler'in üçüncü yasasında karışımıza çıkan ifadeyi elde etmiş olacağız.
r3T2=GM4π2\Large \frac{r^3}{T^2}=\frac{GM}{4\pi^2}
Burada denklemin sağ tarafındaki ifadenin kk gibi bir sabite eşit olduğuna dikkat edin. Aslında burada MM ifadesi (M+m)(M+m)'dir. Fakat gezegenlerin kütlesi, Güneş'in kütlesinin yanında bir hayli ihmal edilebilir kalır. Yine de tabloda en sağda verilen değerlerdeki gibi, ufak farklılıklar görmek mümkün.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 12
- 6
- 2
- 1
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- E. Chaisson. (2013). Astronomy Today. ISBN: 9780321901675. Yayınevi: Addison-Wesley.
- A. Hobson. (1998). Physics: Concepts And Connections. ISBN: 9780130953810. Yayınevi: Prentice Hall.
- D. L. Goodstein. (2013). Feynman’ın Kayıp Dersi. ISBN: 9786051067230.
- C. Yıldırım. (1995). Bilimin Öncüleri. ISBN: 9789754030143. Yayınevi: TÜBİTAK Popüler Bilim Kitapları.
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 27/04/2024 03:06:35 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12862
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.






