Genel Görelilik: Jeodezik Eğri

Bir düzlem üzerindeki iki nokta arasındaki en kısa yol, bir doğru ile temsil edilir. Bir küre üzerindeki iki nokta arasındaki en kısa yol ise, merkezi kürenin merkezi olan ve bu iki noktadan geçen yay parçası ile ifade edilir. Bir yüzey üzerinde yer alan iki nokta arasındaki en kısa mesafeyi belirten bu eğriye, jeodezik eğri diyoruz.

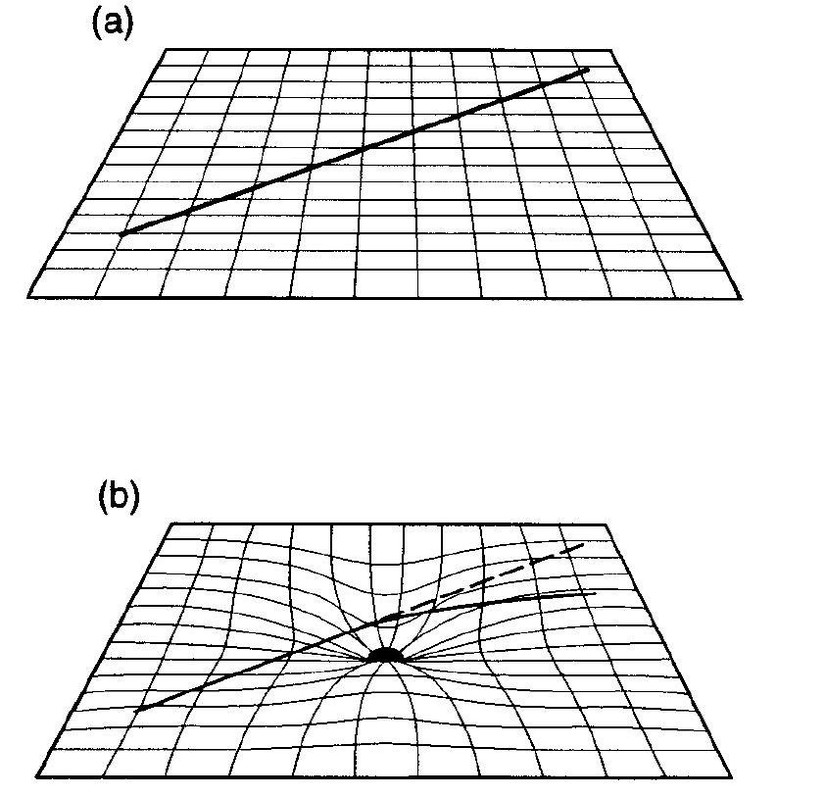
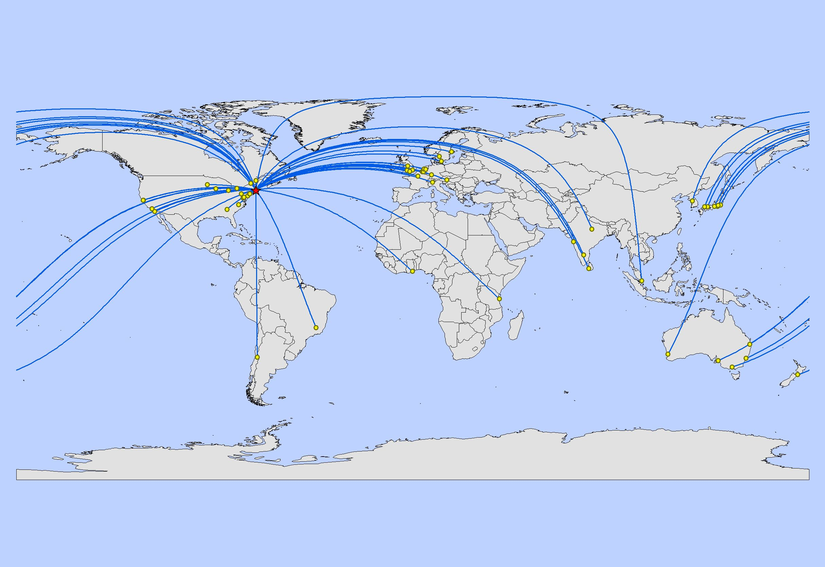
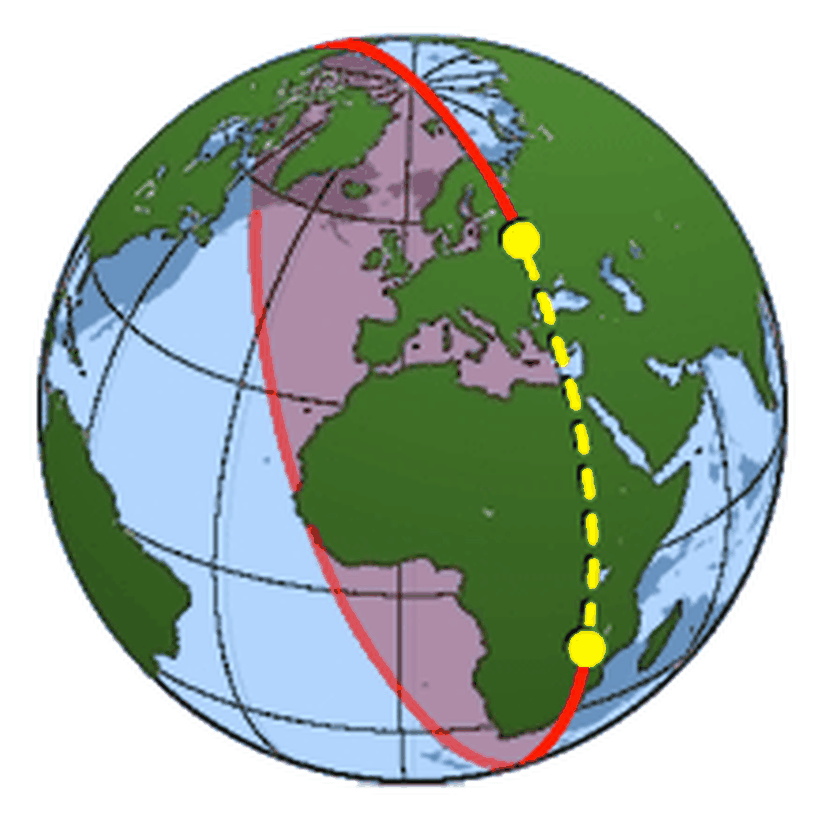
Kütleler, uzay-zamanı kütleleri ile orantılı olarak bükerler. Bu eğri üzerinde bulunan herhangi bir gök cisminin rotası, yani evren çizgisi, bir jeodezik eğridir. Özetle, kütle çekimsel alanda hareket eden bir cisim, jeodezik olan bir evren çizgisini takip eder.

Bir düzlem üzerinde iki nokta arasındaki en kısa mesafe bir doğru parçası ile ifade edilirken (a), eğri uzay zamanda bu bir jeodezik eğridir (b).

Bu durum gündelik yaşantımızda uçaklarda karşımıza çıkar. Haritalar, üç boyutlu olan Dünya’nın, iki boyuta indirilmiş hali olduğundan, topolojik olarak bir aldatma yaşatır. Harita üzerinde uçak rotalarını incelediğimizde, uçakların dümdüz gitmek yerine, bir eğri izlediğini görürüz. Aslında bu durum, haritanın iki boyuta indirgenmesinden kaynaklanır. Rotayı Dünya üzerinde düşündüğümüzde, aslında bu eğri, iki nokta arasındaki en kısa mesafe olan jeodezik bir eğridir.

Great_circle_fligth_route — Uçak rotaları

Eğer bu haritayı bir küre üzerine yerleştirecek olursanız, bu eğriye dik ve bakış doğrultusu Dünya’nın merkezini hedef alan bir açıda baktığınızda, jeodezik eğriyi, bir doğru şeklinde görürsünüz. Çünkü bükülmenin olduğu yön, bakış doğrultunuzla aynı yöndedir. Bu sebeple, eğriliği fark edemezsiniz. Fakat bakış açınız biraz değiştiğinde, eğrilik fark edilir olur.

Bir küre üzerindeki en kısa mesafe, merkezi, kürenin merkezi olan ve bu iki noktadan geçen bir büyük çemberin yay parçası ile ifade edilir.

Merkezi kürenin merkezi olup, bu iki noktadan geçen çembere, büyük çember diyoruz. Uçak rotalarına dikkatle bakacak olursanız, aynı boylam üzerinde bulunan rotalarda bir eğrilik yoktur. Çünkü küre, iki boyuta indirgenirken boylamlar bu durumdan etkilenmez. Benzeri şekilde, Ekvator çizgisi de bir büyük çember olduğundan, rota yine kendisidir.

Diferansiyel Geometride Jeodezik Eğri

Jeodezik eğri kavramı, diferansiyel geometride karşımıza çıkar. Bir eğri, üç boyutlu uzay için, burulma ve bükülme ile ifade edilir. Bir düzlem üzerindeki eğriliği bükülme, bu düzleme dik olan diğer düzlemdeki eğriliği ise burulmadır. Doğru üzerinde yaptığımız bu bükme ve burma işlemi sonucu elde ettiğimiz eğri, değişimi ifade eden diferansiyeller ile kolayca ifade edilebilir.

Bir yüzey üzerindeki birim hız eğrisi için, ivmenin yüzey-tanjant bileşeninin uzunluğu, $\text{K}_\text{g}$ , jeodezik eğridir. $\text{K}_\text{g}=0$ olan eğriler, jeodezikler olarak adlandırılır. Parametre gösterimi $\alpha \text{(t)}=x(u(t),v(t))$ olan bir eğri için, jeodezik eğri aşağıdaki şekilde ifade edilir.

(1) $\begin{equation*} \text{K}_\text{g}= \sqrt{2}{\text{EG-F}^2}\\ \Big[-\Gamma^2_{11} u^{'3}+ \Gamma^1_{22} v^{'3}-(2 \Gamma^2_{12}-\Gamma^1_{11})u^{'2}v^{'}\\ +(2\Gamma^1_{12}-\Gamma^2_{22})u^{'}v^{'2}+u^{''}v^{'}-v^{''}u^{'}\Big]\\ *(\text{E}u^{'2}+2\text{F}u^{'}v^{'}+\text{G}v^{'2})^{-3/2} \end{equation*}$

Ögetay Kayalı

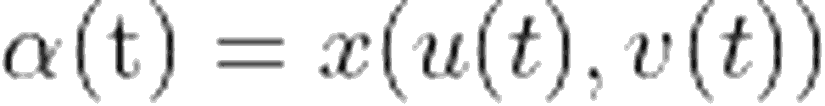
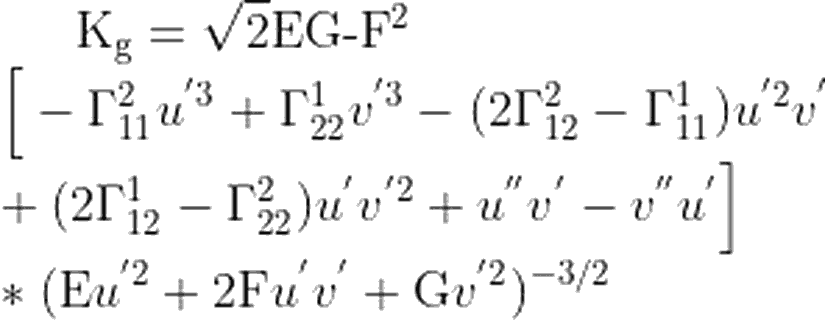
Kaynaklar
1. http://mathworld.wolfram.com/GeodesicCurvature.html
2. Salim Yüce, Diferansiyel Geometri, 4.4 Hiperyüzeyler Üzerinde Geodezik Eğriler, Syf. 189-192

Etiketler