Hanoi Kuleleri ve Çözümü

- Özgün

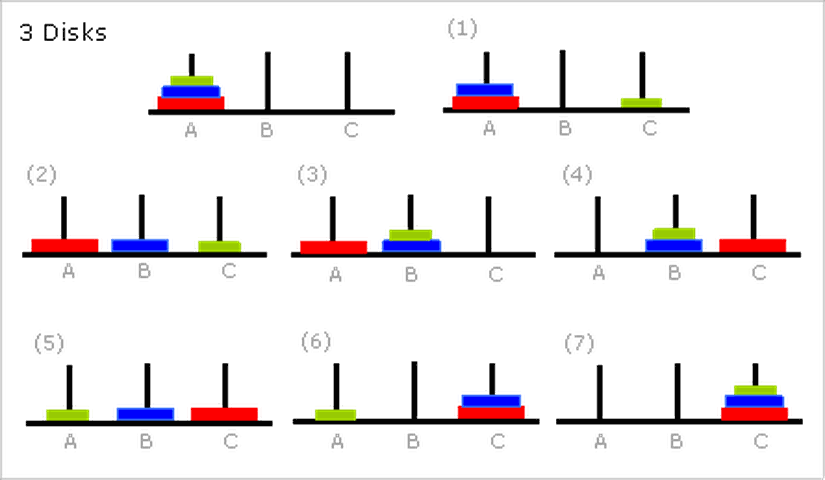
İki diskte, iki diski de sağ tarafa almak istiyorum. Öyleyse önce bir disk için problemi çözmeliyim. Bir disk için problemi çözdüğümde, geriye fazladan olan ikinci disk kalacak. Bunu da hedef konum olan, sağ sütuna koyabilirim. Öyleyse bir disk için problemi, ortada çözmeliyim.
Aynı mantığı üç disk için düşünelim. Üç diski sağ tarafa taşımak istiyorum. Öyleyse iki diski ortada toplamalıyım ki, fazladan olan en büyük disk sağ tarafa gelebilsin. İki diski ortada toplayabilmek için ise, bir üstteki adımın geçerli olduğunu göreceksiniz. Küçük olanı en sağa almalıyım ki, ikinci disk ortaya gelebilsin. Bu yüzden, üç diskli problemde, ilk hamle en sağa koyarak başlıyor.
Üç diskli problemin çözümünde, ilk hamlenin, bir diskli problemin çözümü, üçüncü hamlenin de iki diskli problemin çözümü olduğuna dikkat edin. Üç disk problemi, yedi basamakta çözüldüğüne göre, dört disk problemini çözerken, yedinci basamakta üç disk problemini çözmüş olmalıyız.
Hanoi Kuleleri
Dört Diskli Problemin Çözümü
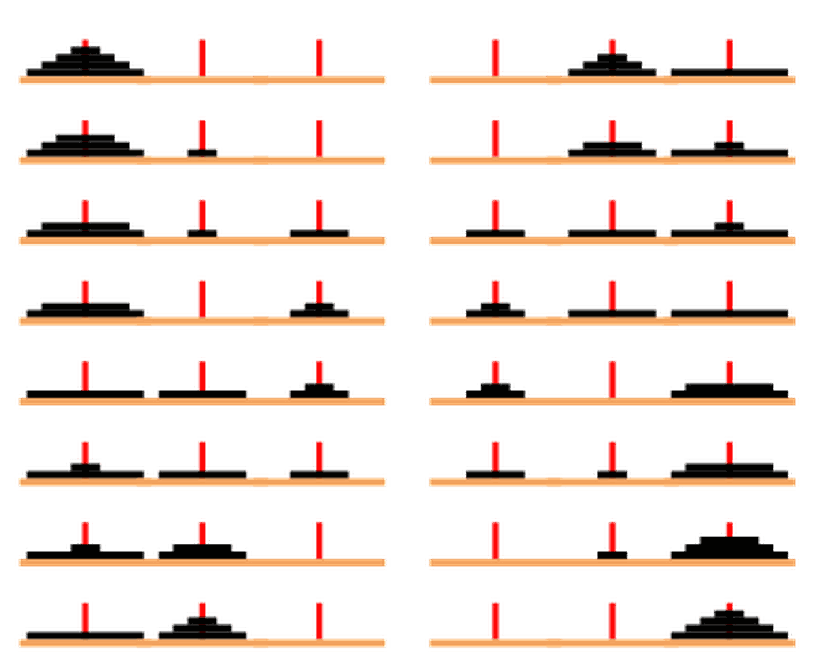
Hanoi kulelerinde dört diskli problemin çözümü de ele aldıktan sonra, konunun rahatça kavranacağını düşünüyorum. Daha önce bahsettiğimiz gibi, ilk önce yapmamız gereken hamleyi bulmalıyız. Bir diskte sağda, iki diskte ortada, üç diskte sağda başlamıştık. Öyleyse dört diskte ortada başlamalıyız. Çünkü en küçüğü ortaya alırsak, bir büyüğünü en sağa alıp, küçüğü de onun üstüne alarak, üç hamlede Hanoi kulelerinin iki disk problemini çözmüş oluruz. Bundan sonra işlem üç disk problemini çözmek olur.Orta kısım boş olduğuna göre, üçüncü disk buraya gelir. En sağdaki küçük disk sola geçer, ortanca ortaya gelir ve küçük tekrar ortaya gelir. Böylelikle üç disk problemi çözülmüş olur ve işte işin açıklaması. Üç disk problemini çözdük ve üç disk de ortada. Böylelikle dördüncü ve en büyük olanı sağa koyabilirim. İşte tam bu sebepten ilk hamleyi ortaya yaptık.
Bu noktadan sonrası, sanki en sağda büyük bir disk yokmuş gibi düşünülerek çözülebilir. Amaç, ortadaki üç diski sağa almaktır. Küçük sağa alınır, ortanca sola, ardından küçük sola, büyük sağa. Böylelikle problem iki diske düşer. Küçük ortaya, büyük sağa, küçük sağa ve problem çözülmüştür.
Formülasyon
Hanoi kulelerinde dört disk problemininin çözümü 15 hamlede gerçekleşti, üç diskin 7, iki diskin 3, bir diskin 1. Burada yakalayacağımız nokta, aslında yukarıdaki algoritmada geçiyor. Dikkatle inceleyelim.Üç diski ortada toplamamız 7 hamle almıştır, bundan sonraki 1 hamle, dördüncü diske sağa almaktır. Sonraki hamle ise, 7 hamlede üç diski, bu en büyük diskin üzerine almaktır. Yani yapılan işlem sayısı 7+1+7=15'tir.
Benzeri şekilde üç disk problemini ele alalım. Üç disk probleminde, ilk 3 hamle ile iki disk problemi çözülür, 1 hamle ile büyük disk hedefe konulur, sonraki 3 hamle ile iki disk üstüne eklenir. Yani yapılan işlem sayısı 3+1+3 = 7'dir.
Yani aslında daha alt problemlere ayrılmış şekilde yazacak olursak, dört disk problemi 7+1+7 şeklinden aşağıdaki şekle gelir.
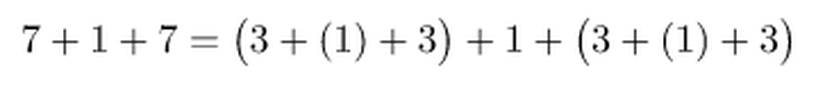
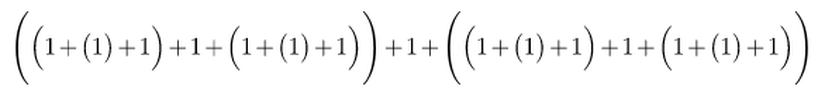
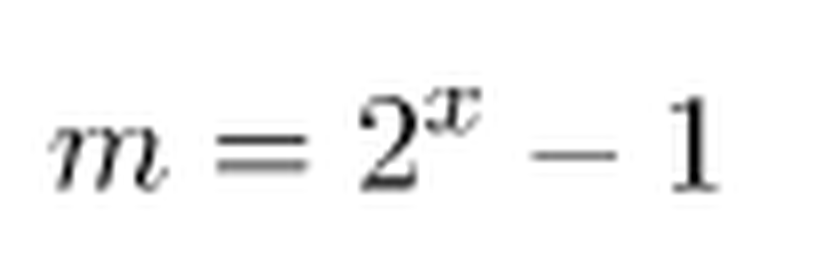
Hazırlayan:Ögetay Kayalı
Referanslar
1. Mathworld Wolfram, <http://mathworld.wolfram.com/TowerofHanoi.html>
Bu yazı ilk olarak 26 Ağustos 2016 tarihinde yayınlanmıştır.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 28/04/2024 23:02:50 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12759
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.


