Gök Cisimleri Neden Eliptik Yörüngelerde Dolanır? Çembersel Yörüngeler Neden Mümkün Değil?
 Newsweek
Newsweek
- Özgün
- Astronomi
Gezegenler ve diğer bütün gök cisimleri, kusursuz olarak görülen çember yerine eliptik yörüngelerde dolanmaktadır. Hiçbir ama hiçbir gök cismini, ne çift yıldızları ne de gezegenleri diğer bir gök cisminin etrafında çembersel bir yörüngede dolanırken göremezsiniz. Çember olmaya çok yakın bir elips olabilir, fakat asla bir çember olmaz.
Yörüngelerin eliptik olması gerektiğini Kepler yasaları sayesinde biliyoruz. Fakat bu yasalar yörüngenin nasıl olduğunu söylüyor, neden böyle olduğunu değil. Dolayısıyla neden çember yörüngelerle karşılaşmadığımızı anlamak için bu yasaların kökenini incelememiz gerekiyor. Daha basit bir yaklaşımda bulunarak örnekler üzerinden gidebiliriz.
Bazı kuyruklu yıldızların yörüngesi açıktır. Bir başka deyişle Güneş'in yanından bir kez geçip bir daha dönmemek üzere giderler. Bir dolanma hareketi yapmazlar. Gezegenlerin hareketini ise kapalı yörüngelerle tanımlarız, çünkü belirli bir dolanma hareketi yaparlar. Sınır da tam olarak burada başlar. Geometrik olarak bu iki yörüngeyi tanımlamak için basıklık (ee) adını verdiğimiz bir parametre tanımlarız.
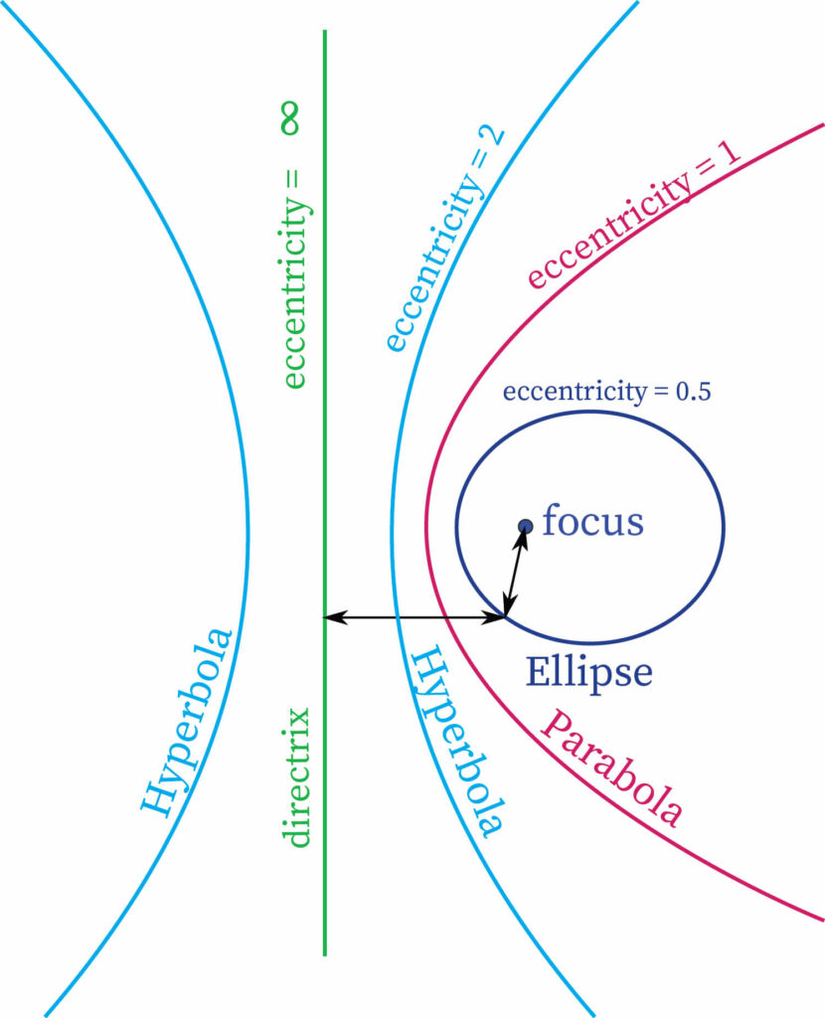 Bartleby
BartlebyEğer e=0e=0 ise bu bir çemberi, eğer 0<e<10<e<1 ise bu bir elipsi, eğer e=1e=1 ise bu bir parabolü, eğer e>1e>1 ise bu bir hiperbolü temsil eder. İddiamız, yani çembersel yörünge açıkça e=0e=0 olmasını gerektiriyor. İlk aklımıza gelen düşünce, ee değerini belirleyen denklemde sıfırın bir şeyleri karıştırıp tanımsız yaptığı ya da daha doğrusu fiziken anlamsız kıldığı bir nokta olabileceğidir. Bu yüzden denklemi incelemekte fayda var. Elimizdeki denklem ise şöyle:
e=1+2EL2mα2\Large e= \sqrt{1+\frac{2EL^2}{m\alpha^2}}
Burada ee basıklık değeri, EE toplam yörünge enerjisi, LL açısal momentum, mm kütle, α\alpha da ters kare yasasından gelen katsayıdır. α\alpha ve LL kompleks sayı olamadıklarından dolayı e=0e=0 değerinin EE parametresine bağlı olduğunu görürüz.E=Ek+EpE=E_k+E_p olduğundan, yani toplam yörünge enerjisi; kinetik enerji ve potansiyel enerjinin toplamı olduğundan negatif bir değer alabilir. Örneğin ISS (Uluslararası Uzay İstasyonu) için hesap yaparsak değerleri şöyle buluruz:
Ep≈−62 MJ/kgEk≈31 MJ/kgE≈−31 MJ/kg\Large E_p \approx -62 \space MJ/kg\\ E_k \approx 31\space MJ/kg \\ E \approx -31 \space MJ/kg
Yani basit bir yaklaşımla yörünge basıklığını belirleyen denkleme baktığımızda herhangi matematiksel bir problem yok gibi görünmektedir. Öyleyse çok daha derinlere inmeden fiziksel yorumlara bir göz atmakta fayda var.
"Çembersel bir yörüngemiz olsaydı, içinde bulunduğumuz durum ne olurdu?" sorusuyla başlayalım. Çembersel yörünge, herhangi bir en yakın ya da en uzak nokta olmadığı anlamına gelir. Yani renberi=reno¨ter_{enberi}=r_{enöte}'dir. Yine Kepler Yasaları'ndan eşit zaman aralıklarında eşit alanların tarandığını biliyoruz ki; gök cismi etrafında dolandığı noktaya yakınlaştıkça hızı artar, uzaklaştıkça azalır. Çembersel yörüngede herhangi bir yakınlaşma-uzaklaşma hareketi olmayacağı için hızın da sabit olması gerektiği sonucuna varırız. Buna bağlı olarak açısal hız, potansiyel enerji ve kinetik enerji de sabit olacaktır.
Cismin yörüngesinin çembersellikten sapmasına sebep olan esas faktör, yörünge hız vektörüne dik olan enine ivmedir. Çembersel bir yörüngede enine ivmenin büyüklüğü sabittir ve hız vektörünün yönü değiştikçe buna dik olarak kendisi de değişir. Bu yüzden yörünge daima çembersel olarak kalır. Merkezcil ivmeden biliyoruz ki, Fm=mV2/rF_m=mV^2/r'dir. Newton'dan da bildiğimiz F=maF=ma'yı uygularsak, ivme için a=V2/ra=V^2/r eşitliğini elde ederiz. VV (hız) sabit olduğuna, rr de sabit olduğuna göre; aa'nın (ivmenin) de sabit olacağı açıktır. Zaten beklentimiz de bu yöndeydi.
Çembersel yörüngenin tüm bu sabitliğinin merkezcil kuvvet olan Fm=mV2/rF_m=mV^2/r ile kütleçekimsel kuvvet olan Fg=GMm/r2F_g=GMm/r^2'den geldiğine dikkat edelim. İki kuvveti birbirine eşitlersek şöyle bir eşitlik buluruz:
Fg=Fm\Large F_g=F_m
GMmr2=mV2r\Large \frac{GMm}{r^2} = \frac{mV^2}{r}
V=GMr\Large V= \sqrt{\frac{GM}{r}}
Bu da bize hızın sabit olması gerektiğini bir kere daha gösterir. Çünkü kütle çekim sabiti olan GG zaten bir sabittir, kütlemiz olan mm yine bir sabittir, yörüngemizin çembersel olması gerektiğinden rr de yine bir sabittir.
Yaptığımız tüm bu gözden geçirmeler, çembersel yörüngenin gerçekleşmesi için gereken koşulları bize söyler. Öyleyse şimdi neler değişirse yörüngenin çembersel olamayacağını açıkça görebiliriz. En çok göze batan parametre hız olduğu için, hızdaki değişimlerin nelere sebep olacağını göz önüne alırsak, sorunun cevabına ulaşabiliriz gibi görünüyor.
Hızın değişmesi, kinetik enerjinin değişmesi demektir. Bu durum yörüngenin toplam enerjisini de değiştirecektir. Yörüngenin toplam enerjisinin doğrudan basıklık değeriyle ilgili olduğunu ilk denklemde göstermiştik. Bu sebeple hızda gerçekleşecek en ufak bir değişiklik doğrudan ee değerini etkileyecek ve yörüngenin çembersellikten çıkmasına, eliptik olmasına sebep olacaktır. Bunu 4. denklemde de test edebilirsiniz. Burada GG ve MM değerleri sabit olduğundan VV'nin değişmesi doğrudan rr'nin değişmesini gerektirir. (Bu denklemin çembersel yörünge kabulünden geldiğini unutmayın, normalde daha farklı bir hal alacaktır.)
Peki hızın değişimine ne sebep olabilir? Öncelikle çembersel yörüngenin bir kabul olduğuna değinelim. Yani çembersel yörünge, işlerin basitçe yapılabilmesi ve denklemlerin kolayca çözülebilmesi için yaptığımız birçok varsayım sonucunda ortaya çıkar. Gerçekler ise böyle değildir. Sistem karmaşıklığı ve çeşitliliği içerisinde barındırır. Dolayısıyla çok farklı etkileşimler gerçekleşir. Bu etkileşimler döngüsel olabileceği gibi, yerel olarak incelendiğinde bir rastgelelik de barındırabilir.
Hepimizin bildiği Güneş Sistemi üzerinden düşünelim. Güneş Sistemi'nde birçok gezegen var ve bunların hepsi farklı kütle ve boyutlarda. Uzaklıkları ve Güneş etrafındaki dolanma periyotları da farklı. Dolayısıyla bize bazen yakın, bazen de uzak oluyorlar. Zaman zaman hiç umulmadık bir şekilde gelip cisimlere çarpan kuyruklu yıldız gibi faktörler de var. Bunun yanında hiçbir gök cismi tam olarak küresel değil. Hatta Güneş, katı bir cisim değil ve çalkantılara sahip.
Dolayısıyla sistemin içerisindeki bütün gök cisimleri sürekli değişen ek kuvvetlerin etkisi altında. Yakınlaşmalar ve çarpışmalar buna doğrudan etki ederken; Güneş'in katı bir cisim olmayışı ve gezegenlerin tam küresel olmayışı da zamana bağlı olarak çekimsel değişimlere sebep oluyor. Bu sebeple gök cisimlerindeki bu kusursuz olmayan çeşitlilik, yine kendi içerisinde çeşitliliğin doğmasına sebep olur. Kusursuz gördüğümüz çembersel sistem ise tekdüze ve aslında ahenk taşımayacak kadar basittir.
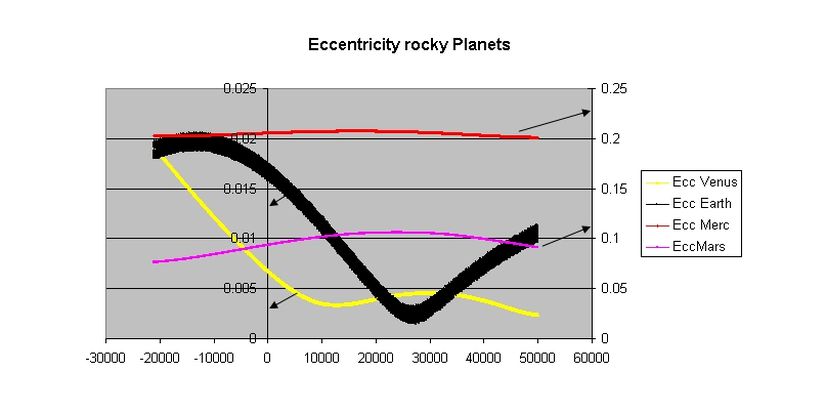
Yukarıdaki grafikten de görüldüğü üzere gezegenlerin basıklık değeri uzun zamanlarda farklı şekillerde değişimler göstermektedir. Dünya için şu anda basıklık değeri e=0.0167e=0.0167 olsa da bu değer 0.0034 ile 0.058 arasında değişmektedir.
Bu değerin çembersel olmaya ne kadar yakın olduğunu görüyoruz. Aslında büyük bir tehlike de burada göze çarpıyor: Eğer yörünge çembersel olursa, hız değişiminin negatif olması durumunda olacakları bir düşünelim. Merkezcil kuvvet etkisi V2V^2 ile doğru orantılı olduğundan, merkezcil kuvvet azalacak ve zaten kütleçekimsel kuvvetle eşit olan bu kuvvet, bir de üstüne azalma gösterdiği için kütleçekim baskın hale gelecektir. Bu da gök cisminin, etrafında dolandığı diğer gök cismi üzerine düşmeye başlaması demektir.
Yani Dünya eğer çembersel bir yörüngeye sahip olsaydı ve bir başka gezegenin ona yakınlaşması sonucu hızı yavaşlasaydı ya da gidiş yönünün aksi yönde çarpan büyük kütleli bir kuyruklu yıldız Dünya'nın hızını yavaşlatsaydı; Dünya yavaş yavaş Güneş'in üzerine düşmeye başlayacaktı. Bu da neden çembersel yörüngeye sahip gök cisimleri görmediğimizi bir kez daha ortaya koyar. Çünkü eninde sonunda bir etkileşime girecek bu gök cismi, etkileşimin sonucunda yok olacaktır.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 6
- 3
- 3
- 2
- 1
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- C. Kılınç. (Akademik Ders Notları). Gök Mekaniği Ders Notları. Not: Ege Üniversitesi Astronomi ve Uzay Bilimleri.
- Ö. Kayalı. Gök Mekaniği: Giriş Ve Temel Kavramlar. Alındığı Tarih: 10 Ocak 2024. Alındığı Yer: DocPlayer | Arşiv Bağlantısı
- S. W. McCuskey. (1963). Introduction To Celestial Mechanics.
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 27/04/2024 00:44:00 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12948
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.




