Genel Görelilik: Einstein Alan Denklemleri

- Özgün
Madde uzay-zamana nasıl büküleceğini, uzay-zaman da maddeye nasıl hareket edeceğini söyler.-J. A. Wheeler
Einstein 1915 yılında yılında yaptığı yayınla, enerji-momentum ile uzay-zaman eğriliği arasında bir ilişki olduğunu ortaya koydu. Yani daha basit bir ifadeyle, madde ile geometri arasında sıkı bir ilişki bulunuyordu. Wheeler'ın sözünde olduğu gibi; madde, uzay-zamanı büküyor ve bükülmüş uzay-zaman da maddeye jeodezikler boyunca hareket etmesi gerektiğini söylüyordu. Bugün bunu ifade eden denklem setine, Einstein Alan Denklemleri diyoruz.
Einstein Alan Denklemleri
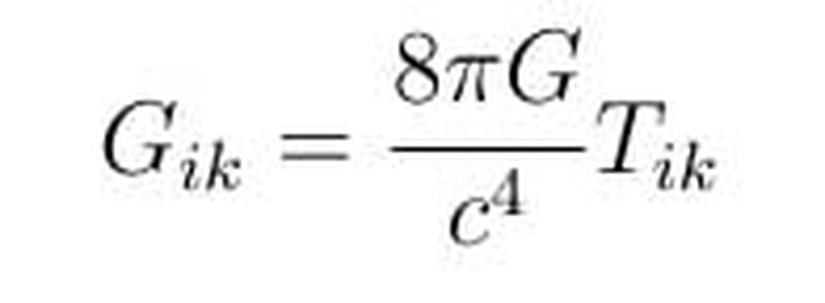
Denklemin sol tarafında yer alan Gik ifadesi, Einstein tensörünü ifade ederken, sağ tarafta yer alan Tik ifadesi stres-enerji (enerji-momentum) tensörünü ifade eder. Yani denklemin sol tarafı geometriyi, sağ tarafı ise maddeyi ifade etmektedir. Denklem sıklıkla aşağıdaki gibi yazılır.
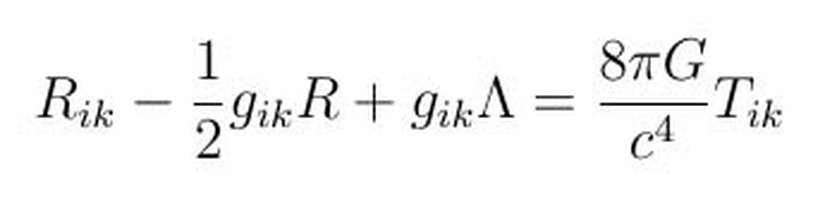
Burada sol taraf Gik'nın açık halini ifade eder. Rik terimi Ricci eğrilik tensörü, gik metrik tensör, Reğrilik skaleri, Λ (lambda) ise kozmolojik sabittir. Bazen Einstein alan denklemlerinin kozmolojik sabitsiz halini de görebilirsiniz.
Burada i ve k alt indisleri, kaç boyutlu uzayda-zamanda çözüm yaptığınıza göre değerler alır (bazen ν ve μ ile de gösterilir). Sıklıkla çözümler dört boyutlu uzayda-zamanda ele alınır ve bunlardan biri zaman, diğer üçü ise uzay bileşenidir. Örneğin kartezyen koordinatlarda (t,x,y,z) koordinatları kullanılır. Bu da i ve k'nın (0,1,2,3) değerlerini alacağını gösterir (bazı yerlerde (1,2,3,4) şeklinde de görebilirsiniz). Bazı kitaplarda notasyon farklı olsa da sıklıkla 0 koordinatı t'ye karşılık gelir, biz de öyle alacağız. Burada bir diğer dikkat edilmesi gereken nokta, zaman bileşeninin işaretinin uzaya göre zıt işaret aldığıdır. Yani eğer (0,1,2,3) notasyonunu kullanıyorsak işaret (-,+,+,+) ya da (+,-,-,-) olarak alınır.
Tek bir denklem gibi görünen bu denkleme neden Einstein alan denklemleri dendiğini indislerden anlayabilirsiniz. i ve k için dörder tane seçenek olduğundan, 4x4=16 farklı denklem olduğu ortaya çıkar. Bunları aşağıda daha açık bir şekilde görebilirsiniz.
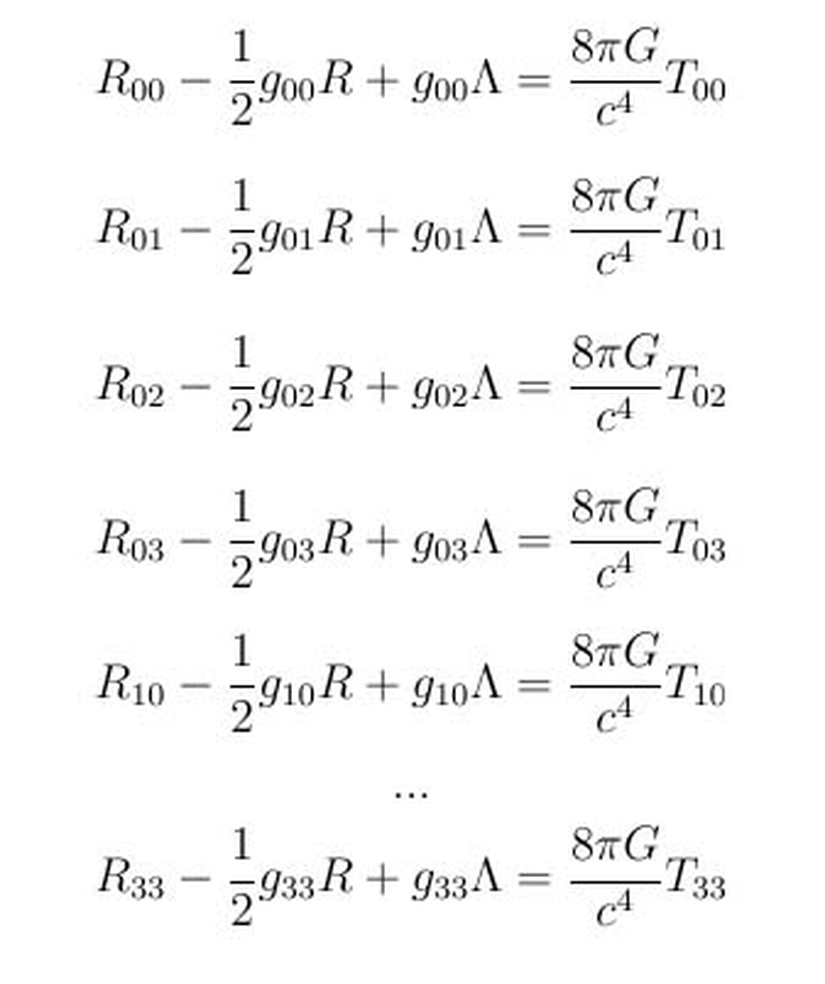
Fakat bunlardan altısı birbirinin aynıdır. Yani toplamda 16 denklem olması gerekirken, simetriden ötürü (matriste üst üçgenseli düşünün), Einstein alan denklemlerinde yalnızca 10 tane farklı bileşeni bulunur. Seçtiğinizi metriğe göre ise, elde ettiğiniz denklem sayısı azalır. Örneğin Schwarzschild çözümünde yalnızca 4 tane denklem ortaya çıkar. Bazen i ve k alt indisleri sayılar yerine, koordinatları ifade eden terimlerle de kullanılabilir. Örneği R00 yazmak yerine, Rtt yazmak tercih edilebilir. Notasyon tercihi size kalmış. Bazen bunlar bir takım kurallara göre kullanılır.
Einstein Alan Denklemlerinin Çözümü
Aslında Einstein alan denklemleri, bize bir diferansiyel denklem seti verir. Mesele bu diferansiyel denklem setini çözerek, tıpkı Newton'ın F=ma'sında olduğu gibi, bir hareket denklemi elde etmektir. Yani Einstein alan denklemlerinin çözümünden, çözümü yapılan geometride maddenin davranışının ne olması gerektiği bulunur. Örneğin boş bir uzayda, dönmeyen, küresel simetrik, yüksüz bir karadelik için Schwarzschild çözümünü elde ederiz. Bu da böyle bir karadeliğin etrafındaki uzay-zamanı nasıl etkilediğini bulmamızı sağlar.
Elde edilen çözüm, koordinat tercihinizden bağımsızdır. Yani kartezyen koordinatları kullanarak yaptığınızda elde ettiğiniz çözüm ile, küresel koordinatları kullanarak yaptığınızda elde ettiğiniz çözüm aynıdır. Dilerseniz başlangıçta koordinat dönüşümü yaparsınız, dilerseniz sonuçta dönüşüm yaparsınız. Aynı sonucu verecektir. Yalnızca burada seçtiğiniz metriğin matrisinin daima tersinin bulunuyor olması gerekir.
Einstein Alan Denklemlerinin Elementleri
Ricci Eğrilik Tensörü
Einstein alan denklemlerinde yer alan Rik, Ricci eğrilik tensörü, aşağıdaki şekilde ifade edilir.
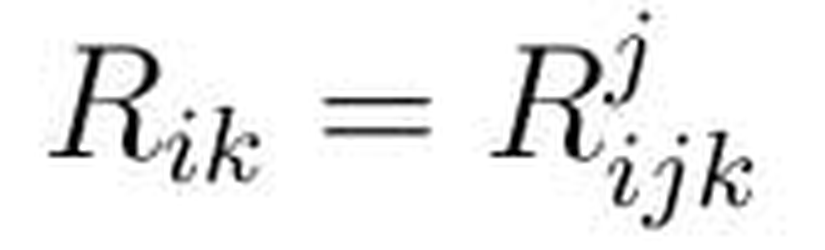
Burada Rlijk Riemann tensörüdür ve Rik'nın hesaplanabilmesi için Rjijk'nın hesaplanması gerekir. Burada i ve k değerleri bizim seçimimiz iken j ve p değeri seçimimizde yoktur. Bunun hesaplanabilmesi için j değerlerinin tümü için toplam alınır.
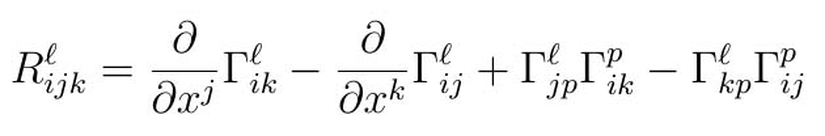
Bu hesaplandığında seçilen i ve k'lar için Rik hesaplanmış olur. Burada oldukça fazla parametre bulunması sebebiyle fazla miktarda sonuç olduğu görülür. i, j ve k değeri için dörder değerden toplamda 64 ifade gelir. Ayrıca her birinin içerisinde dört değer daha alan p değeri üzerinden toplam alınmalıdır, bu da 256 değer yapar. Fakat bunların çoğu sıfırdır. Özellikle Schwarzschild ve Friedmann çözümlerinde hatta çoğunda 10 bileşenin tamamı bulunmaz. Genellikle Rtt, Rrr, Rθθ, RΦΦ bileşenleri sıfırdan farklıdır. Böyle bir durumda i=k olduğu görülür, bu da hesabı tekrar 64 parametreye düşürür. Fakat, dönen bir karadelik için tanımlı metrik olan Kerr metriğinde, dönmenin sebep olduğu açılar da devreye girerek bu sayıyı artırır. Bu yüzden metriğin davranışını anlamak, hesabı anlamak adına önemlidir.
Christoffel Sembolü
Yukarıda Riemann tensöründe yer alan ifade olan Gamma ikl ise Christoffel sembolüdür ve kabaca metrik bağlantıyı inceler. Bağıntısı aşağıdaki gibi verilir.
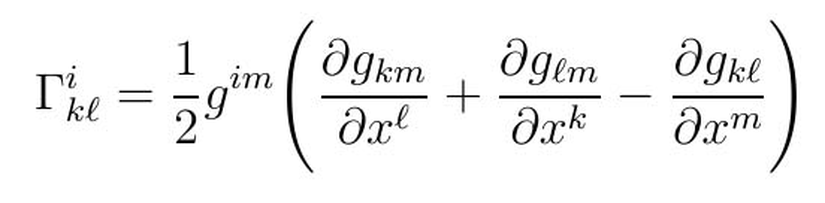
Burada m değeri üzerinden toplam alınır. Her bir parametre eğer tek tek denenirse; i, k, l ve m değerlerinin her biri için 4 değer bulunduğundan, toplamda 4x4x4x4=256 tane Christoffel sembolünün hesaplanması gerektiği görülür. Fakat bunların da bazıları simetriktir ve aynı değeri verir (örneğin k ve l'nin yerini değiştirirseniz ifade değişmez). Ayrıca seçilen metriğe göre, çoğunun değeri sıfır çıkacaktır. Örneğin metriğiniz sadece Rtt, Rrr, Rθθ, RΦΦ değerlerini barındırıyorsa, gim değerinde i=m olmalıdır. Bu da Christoffel sembölünde i=m için çözüm yapmanızın yeterli olduğunu, gerisinin zaten sıfır çıkacağını gösterir. Bu gibi çıkarımlarla yapılan hesap sayısı oldukça aşağıya çekilebilir.
Özetle göz korkutuyor gibi görünse de çoğu değer bu şekilde sıfır çıkmaktadır. Basit yaklaşımlarla ve dikkatli bir hesaplamayla diferansiyel denklem setine ulaşılabilir. Mesele diferansiyel denklemleri çözebilmektir ya da seçtiğiniz metriğin zorluğuna göre bunu düzenleyebilmektir. Elbette günümüzde bunları elle tek tek çözmek yerine, Mathematica gibi programlama dilleriyle kolaylıkla gerekli denklemlere ulaşabiliyoruz. Fakat bunlar işin sadece hamallık kısmını ortadan kaldırıyor.
Ricci Eğrilik Skaleri
Eğrilik skaleri ise, adından anlaşılacağı üzere herhangi bir vektörel bileşene sahip değildir, yani sıfırıncı mertebeden bir tensördür. Birinci mertebeden bir tensörün ise bir vektör olduğunu hatırlayın. Eğrilik skaleri aşağıdaki gibi ifade edilir.
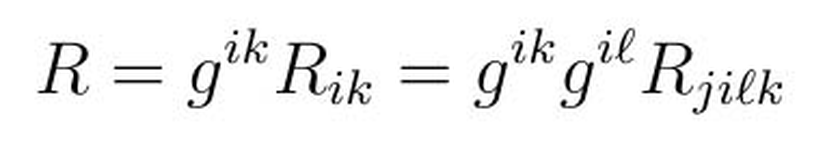
Metrik Tensör
Metrik tensör (ya da basitçe metrik), seçtiğiniz uzay-zaman koordinatlarının geometrik yapısını ifade eder. Daha basit bir deyişle, tanımladığınız uzay-zamanda iki nokta arasındaki geometrinin nasıl olduğunu anlatır. Örneğin Schwarzschild metriği aşağıdaki gibi tanımlıdır.
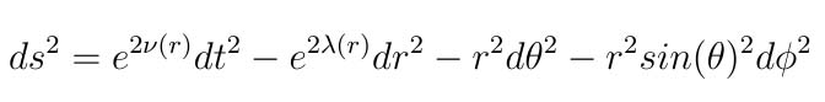
Bu metrikte verilen uzay-zamanda iki nokta arasındaki ayrılığın (ds); dtdt, drdr, dθdθ ve dΦdΦ bileşenleri ile ifade edildiğini görüyoruz. Dolayısıyla metrik tensörümüz aşağıdaki gibi olur.
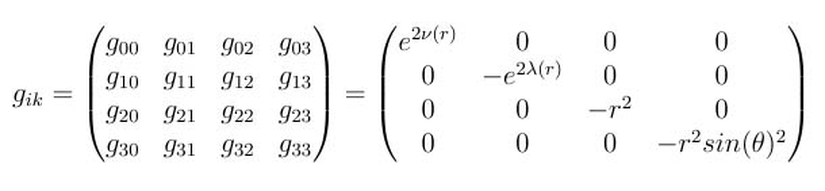
Metrikte dtdr gibi bir ifade olmadığından g01 0'a eşittir. Yalnızca köşegen elemanlarının sıfırdan farklı olduğunu görüyoruz. Fakat bu her zaman böyle değildir. Örneğin Kerr metriğinde dtdΦ terimi de bulunur, yani g03'ün bir değeri vardır.
Hazırlayan:Ögetay Kayalı
Referanslar
1. Kadri Yakut, Ege Üniversitesi Astronomi Bölümü, Extragalactic Astronomy ders notları
2. Misner, Thorne & Wheeler, Gravitation, Wiley.
3. Marko Vojinovic, Schwarzschild Solution in General Relativity
<http://gfm.cii.fc.ul.pt/events/lecture_series/general_relativity/gfm-general_relativity-lecture4.pdf>
4. Heinicke & Hehl (2015). Schwarzschild and Kerr Solutions of Einstein's Field Equations
<https://arxiv.org/pdf/1503.02172.pdf>
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 20/04/2024 06:54:27 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12792
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.


