Kozmik Mikrodalga Arkaplan Işıması'nın (CMB) Kuvvet Tayfı Nasıldır?
 Physics World
Physics World
- Özgün
- Fiziksel Kozmoloji
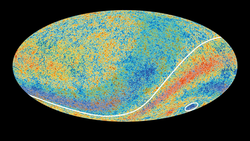
Kozmik mikrodalga arkaplan ışınımı (CMB), evrenin yaklaşık 380.000 yıl yaşındaki halinden arta kalan ve günümüzde gökyüzünün her bölgesinden yaklaşık 2.73 K sıcaklıkta ölçtüğümüz bir mikrodalga ışınımıdır. Bu cümledeki en önemli ifade, yaklaşık 2.73 K ifadesi, çünkü bu ışınımın gökyüzündeki dağılımı incelediğimizde, mikrokelvin (0.001 K) düzeyinde sıcaklık dalgalanmaları olduğunu görüyoruz. Bu dalgalanmaların analizini de kuvvet tayfı ile yapıyoruz. Yani Hubble sabiti, evrenin yoğunluğu (baryonik madde yoğunluğu, karanlık madde yoğunluğu), evrenin geometrisi, evrenin yaşı gibi kozmolojik parametreler hakkında edindiğimiz bilgiler, CMB'deki sıcaklık dalgalanmalarının analizine dayanıyor.
 Phys.org
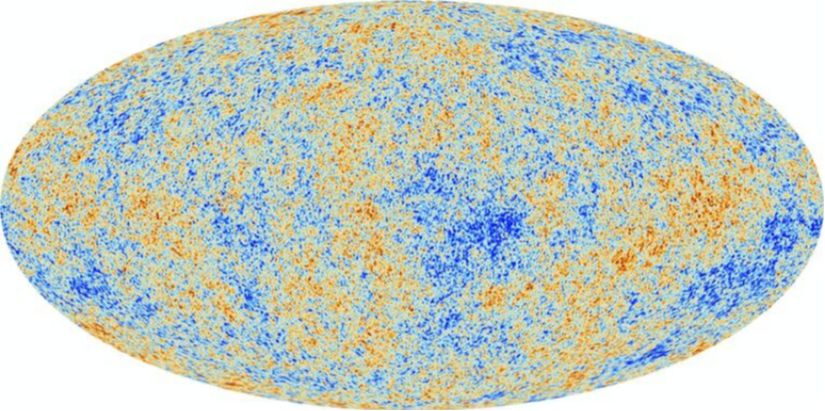
Phys.orgYukarıdaki CMB haritasından da görüldüğü üzere, CMB üzerinde bazı bölgeler diğerlerine göre daha soğukken bazıları da diğerlerine göre daha sıcaktır (mavi ve kırmızı bölgeler). Fakat ortalamaya baktığınızda 2.73 K'lik bir sıcaklık görülür, bu dalgalanmalar yalnızca mikrokelvin (0.001 K) düzeyindedir. Buna rağmen, bu görüntü evrenin dinamiği hakkında oldukça önemli bilgiler taşır.
Fourier analizinden bildiğimiz üzere fonksiyonlar, ayrı ayrı dalga fonksiyonları şeklinde ifade edilebilir. Fizikte bunu yapmaktaki amaç, gerçekleşen fiziksel olayları ayrı ayrı ele alabilmektir. Her dalga, ayrı bir anlam taşır. Üst üste binmiş bin dalgayı tek seferde anlamak mümkün olmadığından, bunları küçük alt parçalara ayırıp bu şekilde her bir parçayı ayrıca anlayarak en sonunda birleştirip bütün hakkında fikir edinebilirsiniz. Fizikte dalga analizi ile yapılan işlem, kabaca bunu ima eder.
CMB her yönden geldiği için, bu dalga analizinin bir küre üzerinden yapılması gerekir. Bunu da Laplace denklemini küresel koordinatlarda çözerek elde ederiz. Bunun çözümü ise küresel harmoniklerdir.
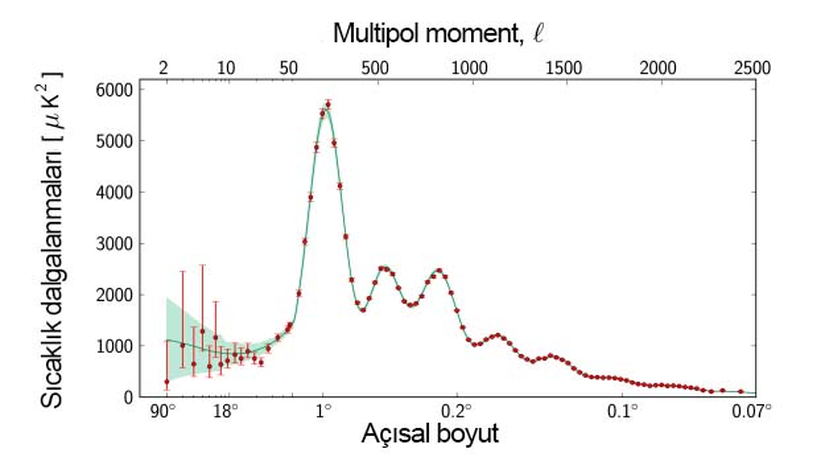
Aslında çoğunluğun da kuantum mekaniğinden aşina olduğu ll ve mm sayıları buradan gelmektedir. Buradaki ll sayısı kabaca, CMB'de gördüğümüz öbeklenmelerin açısal boyutuna denktir. ll sayısı ne kadar büyükse, CMB'de incelenen öbeklenmenin boyutu da o kadar küçüktür. Sonuç olarak, açısal boyuta (ya da multipol moment ll'ye) karşılık, sıcaklık dalgalanmalarının karesinin grafiği çizildiğinde, kuvvet tayfı (İng: "power spectrum") elde edilir. Buradaki kuvvet kelimesi, üstel bir fonksiyon kullanılmasından gelir. Bu yüzden burada "power" kelimesini "güç" olarak değil, "kuvvet" olarak çevirmek gerekir ve bu bizim bildiğimiz kuvvet kavramına değil, bir sayının kuvveti, üssü anlamına gelir.
Kuvvet Tayfı
Aşağıdaki grafikte de görüldüğü üzere, farklı değerlere karşılık gelen çeşitli pikler ve bunların farklı genlikleri söz konusudur. Örneğin ilk pikin l≈220l\approx220 değerine karşılık geldiği görülmektedir (Bu değer, gökyüzünde kabaca 1 derecelik açısal boyuta karşılık gelir). İlk pikin bu değerde olması, evrenin düz bir geometriye sahip olduğuna işaret eder. Eğer l>220l>220 olsaydı, yoğunluk parametresinin değeri 1'den daha küçük olurdu, yani evren açık bir geometriye sahip olurdu. Benzeri bir şekilde eğer l<220l<220 olsaydı, bu da evrenin kapalı bir geometriye sahip olduğuna işaret edecekti. Yani ilk pikin konumu, evrenin geometrisi hakkında bir bilgi taşımaktadır.
 University of Birmingham
University of BirminghamAynı zamanda grafikteki noktaların sayısı, grafikte daha büyük ll değerlerine (daha küçük açısal boyutlara) gidildikçe artmaktadır. Bu durum, istatiksel analiz ile alakalıdır. CMB'yi çeşitli büyüklükte parçalara bölerken daha küçük parçalara böldüğünüzde, parçacık sayınız daha fazladır ve bu da istatistiksel hatanın daha az olacağı anlamına gelir. Başlangıçtaki değerlerde ise, örneğin l=2l=2 için (90 derecelik bir alan için) gökyüzünü yalnızca birkaç parçaya bölebilirsiniz. Burada istatistiksel hata fazla olacaktır. Bunu bir ülkedeki seçim sonucunu, on kişilik bir anketle belirlemeye çalışmak olarak düşünebilirsiniz. Ne kadar çok kişiye sorarsanız, o kadar kesin sonuç elde edersiniz. Yani gökyüzünü ne kadar çok parçaya bölerseniz, hatanız o kadar azalır. Grafiğin sol tarafındaki mavimsi-yeşilimsi bar bu durumdan kaynaklı hatayı gösterir ve kozmik varyans olarak adlandırılır.
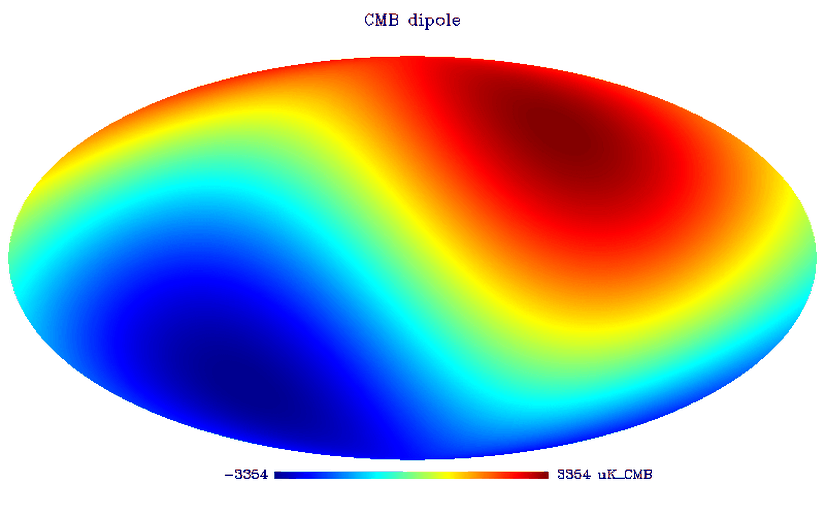
Kuvvet tayfına bakıldığında dikkat çeken şeylerden biri, l=2l=2 değerinden başlamasıdır. Oysa ki l=0l=0 ve l=1l=1 değerleri de mevcuttur. l=0l=0 (monopol) momenti, basitçe tüm gökyüzündeki sıcaklık dalgalanmasının ortalamasını ima eder. Fiziksel açıdan önemli bilgiler taşımasına karşın, değerini belirlemek kozmik varyans sebebiyle zordur. l=1l=1 dipol momenti ise, CMB'nin durgun referans sistemine göre uzaydaki hareketimizi ifade eder. İçerisinde bulunduğumuz uzayda bir hareketimiz olduğundan, bir yönden gelen CMB fotonları kırmızıya kayarken, diğer yönden gelenler maviye kaymaktadır. Dipol momentinin haritası aşağıdaki gibidir.
 University of Cambridge-Institue of Astronomy (M. Pettini)
University of Cambridge-Institue of Astronomy (M. Pettini)Kuvvet Tayfının Biçimi
Kuvvet tayfının biçimi, bize kozmolojik parametrelerin ne olması gerektiğini söyler. Böylelikle sadece CMB'ye bakarak (ve elbette ona oldukça karmaşık analizler uygulayarak), evren hakkında bilgi edinebiliyoruz.
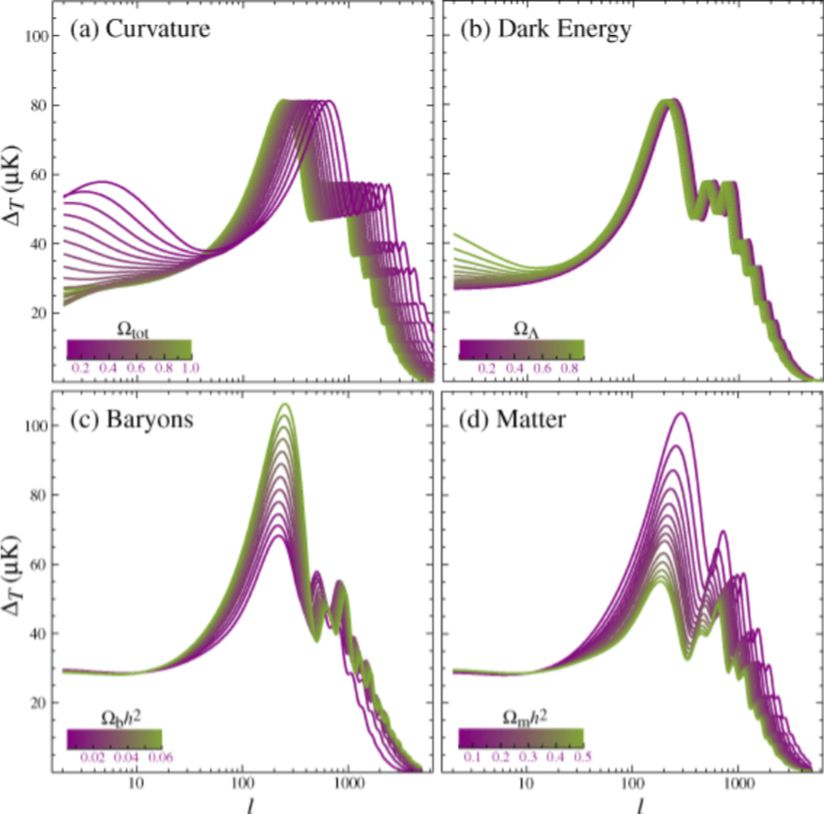 Professor, Department of Astronomy and Astrophysics University of Chicago
Professor, Department of Astronomy and Astrophysics University of ChicagoYukarıdaki çalışmada; (a) evrenin geometrisi, (b) karanlık enerji yoğunluğu, (c) baryonik madde yoğunluğu ve (d) madde yoğunluğu parametrelerinin değişimi durumunda, kuvvet tayfının biçiminin nasıl değiştiği gösterilmiştir. (a) grafiği, daha önce de bahsettiğimiz gibi l≈220l\approx220'de olan ilk pikin, toplam yoğunluk azaldıkça l>220l>220 bölgesine kaydığını göstermektedir. Toplam yoğunluğun azalması (1'in altına düşmesi) demek, evrenin açık bir geometriye sahip olacağı anlamına gelir. Dolayısıyla yeşil eğri düz bir evren için kuvvet tayfını, mor eğri ise açık bir evren için kuvvet tayfını gösterir. Düşük-ll değerleri bölgesinde, grafiğin sadece ötelenmekten ziyade, bir pik yapması gerektiği de görülmektedir. Fakat elde ettiğimiz kuvvet tayfı böyle bir bilgi taşımıyor. Bu sebeple, elimizdeki verilerin evren için düz bir geometriye işaret ettiğini söyleyebiliyoruz.
Benzer şekilde (b) grafiğinde karanlık enerji yoğunluğu azaldıkça, grafiğin sağ tarafa doğru ötelendiği görülmektedir. Günümüzde Planck 2015 sonuçlarına göre karanlık enerji yoğunluğu 0.69 olarak belirlenmiştir. Ayrıca yüksek karanlık enerji yoğunluğunun kuvvet tayfında düşük-ll değerlerinde kendini belli ettiği de görülmektedir. (c) grafiğinde baryonik madde yoğunluğu arttıkça, ilk pikin değerinin arttığı, ikincisinin azaldığı görülmektedir. Kabaca tek sayılı pikler artarken, çift sayılılar azalmaktadır.
Evrenin Başka Bir Yerinden CMB'yi Gözlemlemek
Evrenin başka bir yerinden kozmik mikrodalga arkaplan ışımasını gözlemleyebilseydik, bu durum çalışmalarımıza çok yardımcı olabilirdi. Göreceğimiz şey, aynı fiziksel sonuçları veren fakat pikseli pikseline eşit olmayan bir harita olurdu. Elimizde bu sefer büyük boyutlu parçacıklar için (düşük-ll değerleri için) daha çok veri olacağından, kozmik varyanstaki hata azaltılmış olurdu.
Bunun nedeni başka bir noktada, haritanın farklı fiziksel sonuçlar vermemesi gerekliliğidir. Çünkü içerisinde bulunduğumuz evren aynı evrendir. Fakat ölçümler sırasında ufak sapmalar olacaktır, bunlar da özellikle düşük-ll değerlerindeki hatayı azaltmamıza yardımcı olabilir. Ne yazık ki henüz böyle bir imkana sahip değiliz ve bu düşük-ll değerleri için hiç de hoşumuza gitmeyen bir hata aralığına sebep oluyor. Grafik, bu aralık içerisinde herhangi bir yerden geçebilir ve tam olarak nereden geçtiğini bilmemek, çıkarım yapmamızın önüne bir engel koyuyor.
İçeriklerimizin bilimsel gerçekleri doğru bir şekilde yansıtması için en üst düzey çabayı gösteriyoruz. Gözünüze doğru gelmeyen bir şey varsa, mümkünse güvenilir kaynaklarınızla birlikte bize ulaşın!
Bu içeriğimizle ilgili bir sorunuz mu var? Buraya tıklayarak sorabilirsiniz.
Soru & Cevap Platformuna Git- 2
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- 0
- H. K. Eriksen. An Introduction To The Cmb Power Spectrum. Alındığı Tarih: 18 Mart 2024. Alındığı Yer: WinthersComing | Arşiv Bağlantısı
- R. Tojeiro. Understanding The Cosmic Microwave Background Temperature Power Spectrum. (16 Mart 2006). Alındığı Tarih: 18 Mart 2024. Alındığı Yer: The Royal Observatory, Edinburgh | Arşiv Bağlantısı
- ESA. Esa Science & Technology - Planck's Power Spectrum Of Temperature Fluctuations In The Cosmic Microwave Background. (1 Eylül 2019). Alındığı Tarih: 18 Mart 2024. Alındığı Yer: ESA | Arşiv Bağlantısı
- W. Hu, et al. (2002). Cosmic Microwave Background Anisotropies. Annual Reviews, sf: 171-216. doi: 10.1146/annurev.astro.40.060401.093926. | Arşiv Bağlantısı
- B. Schmidt, et al. Anux: Astrophysics: Cosmology. Alındığı Tarih: 18 Mart 2024. Alındığı Yer: edX | Arşiv Bağlantısı
- P. A. R. Ade, et al. (2016). Planck 2015 Results - Xiii. Cosmological Parameters. Astronomy & Astrophysics, sf: A13. doi: 10.1051/0004-6361/201525830. | Arşiv Bağlantısı
Evrim Ağacı'na her ay sadece 1 kahve ısmarlayarak destek olmak ister misiniz?
Şu iki siteden birini kullanarak şimdi destek olabilirsiniz:
kreosus.com/evrimagaci | patreon.com/evrimagaci
Çıktı Bilgisi: Bu sayfa, Evrim Ağacı yazdırma aracı kullanılarak 16/04/2024 16:08:38 tarihinde oluşturulmuştur. Evrim Ağacı'ndaki içeriklerin tamamı, birden fazla editör tarafından, durmaksızın elden geçirilmekte, güncellenmekte ve geliştirilmektedir. Dolayısıyla bu çıktının alındığı tarihten sonra yapılan güncellemeleri görmek ve bu içeriğin en güncel halini okumak için lütfen şu adrese gidiniz: https://evrimagaci.org/s/12625
İçerik Kullanım İzinleri: Evrim Ağacı'ndaki yazılı içerikler orijinallerine hiçbir şekilde dokunulmadığı müddetçe izin alınmaksızın paylaşılabilir, kopyalanabilir, yapıştırılabilir, çoğaltılabilir, basılabilir, dağıtılabilir, yayılabilir, alıntılanabilir. Ancak bu içeriklerin hiçbiri izin alınmaksızın değiştirilemez ve değiştirilmiş halleri Evrim Ağacı'na aitmiş gibi sunulamaz. Benzer şekilde, içeriklerin hiçbiri, söz konusu içeriğin açıkça belirtilmiş yazarlarından ve Evrim Ağacı'ndan başkasına aitmiş gibi sunulamaz. Bu sayfa izin alınmaksızın düzenlenemez, Evrim Ağacı logosu, yazar/editör bilgileri ve içeriğin diğer kısımları izin alınmaksızın değiştirilemez veya kaldırılamaz.



