Bir Maddenin Sıcaklığı Kütlesini Etkiler Mi?

Bir maddenin sıcaklığı kütlesini etkiler mi?Neredeyse tüm kimyaya giriş ve fiziğe giriş ders kitaplarında bu soru ile ilgili bulabileceğimiz cevap "hayır" şeklindedir. Düşük hassasiyette bir gözlemde sisteme enerji verildiği zaman kütledeki değişimi, aslında enerji verdiğimiz için olan kütle artışını gözleyemeyiz. Tabiidüşük hassasiyette...

Burada maddenin sıcaklık ile faz değişimi (madde halleri arası geçiş) ya da hacimsel değişimini (genleşme vs.) değil, miktar ve enerjisi ile ilgili bir nicelik olan ve klasik fizikte değişmez kabul edilen kütlenin, bir maddenin ortalama moleküler kinetik enerjisinin ölçüsü olan sıcaklık ile değişimini ele alalım. Çünkü kütle ve enerji eşdeğerini biliyoruz. Başlıktaki sorunun gerçek cevabı "evet" olmalıdır.

Sıcaklığın Kütleye Etkisi

Kütle enerjinin farklı bir formudur ve dışarısı ile enerji (ve dolayısıyla madde) alışverişi içerisinde olmayan kapalı bir sistemde sıcaklığı arttırırsak kütleyi de arttırmış oluruz. Tipik bir sistemde bu artış çok düşüktür. Örneğin, belli bir enerji değerindeki 1 kg suyu buharlaştırmadan ısıtmak için 4 kJ bir enerji verirsek m=E/c² bağıntısından 4.4 x 10^-14 kg'lık bir kütle artışı gerçekleşir. Bu, ölçebileceğimiz hassasiyetin epey ötesinde bir değişim.

Daha sıcak olan cisimlerin diğer özdeşlerine göre daha kütleli olmalarının sebebi, kütle enerji eşdeğerinden ileri gelmektedir, yani E=mc²'den. Genel görelilikte kütle çekim kuvveti, enerji ve momentumun uzay-zaman dokusundaki yoğunluk ve akışını belirleyen stres-enerji tensörüne (tensör: Fizikteki büyüklüklerin aralarındaki doğrusal ilişkiler için tanımlanır) bağıdır. Daha açık bir şekilde bu tensör, cismin toplam enerjisini ifade eder. Sıcaklık farkı da maddenin içindeki atom ve moleküllerin hareketi bazında kinetik enerjideki farkı işaret eder.

Elimizde 0°C'de birer litrelik iki durgun su kütlesi bulunduğunu varsayalım. Bunlardan birinin sıcaklığını 100°C'ye getirirsek sıcak olandaki kütle değişimi

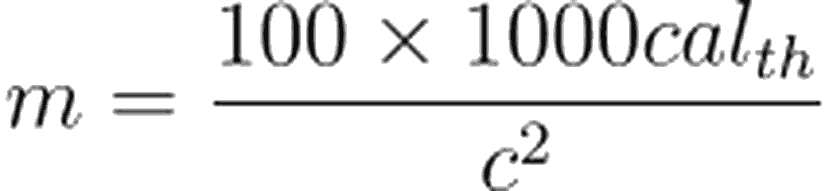
ifadesinden 4.6 nanogram (ng) olacaktır. Yani 100°C'deki su 0°C'dekinden 4.6 nanogram fazla kütleye sahip olacaktır.
Not: Eşitliğin pay kısmı sıcaklığı bilinen bir suyun termokimyasal kalori (enerji birimi) hesabıyla enerji boyutuna dönüşümüdür.

Tabii bu 4.6 ng'lık artışı sorunsuz bir şekilde elde edebilmenin de bazı şartları vardır. Isıtılan su, görülür bir kaynama olmasa da, daha düşük sıcaklıktaki suya göre genleşecek ve daha çok hava ile yer değiştireceğinden soğuk sudan daha hafif ölçülebilir. Bu durum sıcaklık, genişleme katsayısı ve ortamdaki hava yoğunluğu ile hesaplanabilir. Kısacası bu tip etkilerden kurtulmak için deney vakum ortamında yapılmalıdır. Katı maddelerde bu etkiler sıvı ve gazlara göre daha az gözükeceğinden, deneyi katılar üzerinde yapmak daha mantıklı olabilir.

Bu ufacık(!) 4.6 ng'da kabaca 154 trilyon su molekülü bulunur. Bu kadar su molekülünün 4.6 ng'lık kütlesi suyun sıcaklığını 100° C'ye çıkarırken harcanan enerji ile eşdeğerdir. 20g'lık küçük bir bilyenin durgun kütlesi yaklaşık 500 kilotonluk bir nükleer bombanın patlamasında açığa çıkan enerjiye eşittir. Zayıf veya kilolu her birimiz ise megatonluk mertebedeki hidrojen bombalarının patlama enerjilerine sahibiz. Buradaki sorun kütlelerimizin miktarından ileri gelen bu enerjilerin kullanılabilir, yayılabilir enerjilere dönüşümünün teknik açıdan oldukça zor olmasıdır.

Yazımızı okuyucularımıza bir soru ile bitirelim. Elimizde bir yay ve lastik bulunsun. Yay ve lastiği serbest halde (denge durumlarında) ve birlikte (aynı anda aynı terazide) tartalım. Daha sonra lastik ile yayı sıkıştıralım. Yay sıkışarak, lastik de gerilerek potansiyel enerjileri artacaktır. Ve şimdi bu şekilde aynı tartıda tekrar tartalım. Çok çok küçük de olsa sistemin kütlesinde bir değişim meydana gelir mi?

Hazırlayan: Emir Haliki

Referanslar

Evrim Ağacı'ndan Mesaj

Neden Desteğe İhtiyacımız Var?

Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor. Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak... Daha fazla göster

Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor.

Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak (yani kendi mesleğimiz doğrultusunda bir iş sahibi olursak) Evrim Ağacı'na zaman ayıramayacağımızı, ayakta tutamayacağımızı biliyoruz. Çünkü az sonra detaylarını vereceğimiz üzere, Evrim Ağacı sosyal medyada denk geldiğiniz makale ve videolardan çok daha büyük, kapsamlı ve aşırı zaman alan bir bilim platformu projesi. Bu nedenle bizler, meslek olarak Evrim Ağacı'nı seçtik.

Eğer hem Evrim Ağacı'ndan hayatımızı idame ettirecek, mesleklerimizi bırakmayı en azından kısmen meşrulaştıracak ve mantıklı kılacak kadar bir gelir kaynağı elde edemezsek, mecburen Evrim Ağacı'nı bırakıp, kendi mesleklerimize döneceğiz. Ama bunu istemiyoruz ve bu nedenle didiniyoruz.

Destek Ol

1. Fourmilab, <http://www.fourmilab.ch/etexts/einstein/E_mc2/www/>