Aristoteles'in Evreni: Dünya Merkezli Evren

Milattan önce 4. yüzyıldayız. Burada hala Platon’un sözü geçiyor. Eski Yunan düşünürleri, astronomik olaylarla ilgilenmeye başlamış ve bir nebze de olsa açıklama istencini başlatarak, gezegen hareketlerinin açıklanmasına ve anlamlandırılmasına olanak sağlayan sistem fikirlerine ulaşmışlar. Böylece gök olaylarını, Yunan Mitolojisi ve dininden ayırmaya başlamışlar, aynı zamanda astronominin mitoloji ve din doğmalarından ayrılmasıyla temellendirmelerini geometriye bağlayarak önemli sistemler kurmuşlardır.

Astronominin temeline geometrinin konulması Pythagoraşçılardan başlar. Platon’un ortaya attığı sistematik duruşla gökyüzündeki hareketlerin düzenli ve dairesel, hızların ise sabit olduğu kabul edilmiştir. Pythagorasçılar, bütün gök cisimlerinin, yani gezegen ve yıldızların (o zamanlar bilinen gök cisimlerinin) küresel olduklarına, dairesel yörüngelerde hareket ettiklerine inanmış, kürelerin arasında bir uyum olduğunu varsayarak gezegenlerin uzaklıklarının bu uyumla ilişkilendirmişlerdir.

Onlara göre gök cisimleri, merkezin etrafında uzaklıklarıyla orantılı bir şekilde hareket etmekteydiler. Yörüngeleri ise hızlarıyla orantılıydı. Platon, iki küreli evren modelini açarken ilk kürenin merkezde bulunan Dünya'mız (yeryüzü), ikincisininse yıldızlar küresi olduğunu söyledi. Tüm bu varsayımlar sonrası evren modelini belirlerken yeryüzünün veyıldızların değişkenliği için şu iddiada bulunuyordu:

‘’Bu iki küre bir günde tam dönüş yapmaktadır. Gezegenler ise bu iki küre arasında hareket etmektedir.’’

Peki ama gezegenlerin tek düzlemde ve art arda hareket ediyor gibi görünmesinin sebebi nedir? Bu soruya Platon’un takipçisi ve evreni geometriyle harmanlama arayışındaki Eudoxus’tan ilk yanıt gelmiştir. Ona göre evren ortak bir merkezde iç içe geçen ve farklı eğilimlerde dönme ekseni olan kürelerden oluşur. Eudoxus’un küre modeli, Kepler'e kadar uzanmıştır. Ancak şu önemliydi: Bu kürelerin sayısı 56'ya kadar gitmeliydi, ki gezegenlerin hareketlerine uygun bir evren modeli elde edilmiş olsun. Bu zorunluluğu fark edense Aristoteles’ti. Aristoteles’in Platon’un bazı kısımlarını ele almadan geçmesi beklenemezdi.

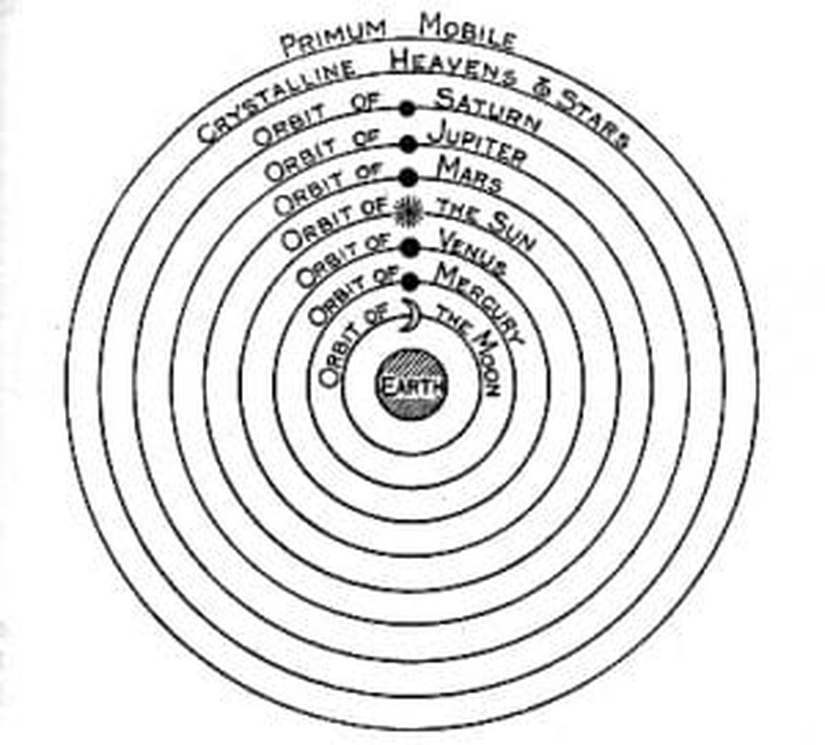
Aristoteles astronomiye dair görüşlerinifizik, metafizikvegökyüzü üzerine adlı yapıtlarında ele almıştır. Aristoteles, Metafizik’in ilk bölümünde kendinden önceki düşünürlerin evren hakkındaki görüşlerini vererek kendi düşüncelerini ortaya koymuştur. Aristoteles’in evren modeli  Eudoxus’un evren modeliydi. Aristoteles’in yeni ve kalıcı düşünce kısımları Copernicus (Kopernik)’a kadar etkin olacak gökyüzü hareketlerinin temel prensiplerini ortaya koymasıdır. Bu diğer bir anlatımla "Yer Merkezli Sistem"olarak adlandırılmıştır.

1. Evren küreseldir ve sonludur.

Aristoteles’in sistematik felsefesiyle bağdaşan bir zorunlulukla, en mükemmel biçimde evren küreseldir. Geometrik olarak bir kürenin merkezi olduğu içinse evren sonludur. Gökyüzü adlı eserinde söyle yazar:

"Gökyüzünün dairesel bir şekil taşıması zorunludur. Çünkü hem varlığına uygun şekil hem de doğaca en önde gelendir.’’ [1]

2. Yer, evrenin merkezinde ve hareketsizdir.

Yer, merkezde bulunmasıyla evrenin merkezi aynı zamanda yerin de merkezidir. Bir tek evren vardır ve bu evren her yeri doldurur. Bu nedenle evren ötesi veya evren dışı yoktur. Yer hareketsizdir. Bu konudaysa Aristoteles Gökyüzü adlı eserinde söyle yazar:

"Şimdi de yeryüzü acaba deviniyor mu yoksa duruyor mu, bunu söyleyelim. Dediğimiz gibi kimisi onu yıldızlardan biri yapıyor, kimi de ortaya koyduktan sonra ortadaki merkez çevresinde sallanıp deviniyordu. Bunun olanaksız olduğu bizim ilkemiz açısından açıkça ortada, çünkü deviniyorsa, ister orta noktanın dışında ister orta noktada olsun, onun bu deviniminin zorla olması zorunlu; bu devinim yerin, toprağın kendi devinimi değil. Yoksa parçalarının her biri devinirdi, oysa bütün parçaları ortaya doğru, düz bir çizgi biçiminde deviniyor, öyleyse yer merkezdedir."

3. Yer, küre biçimindedir.

"…Onun küre şeklinde olması zorunlu(dur). Yer, ya kendi başına küre biçimindedir ya da doğası gereği küre biçimlidir… Görülen nesnelerin aracılığıyla bu açıkça anlaşılır. NitekimAy tutulmalarında her zaman belli bir içbükey çizgi vardır. Dolayısıyla Ay tutulması, yeryüzünün arada kalmasıyla oluyorsa, bu şeklin küre şeklinde olan yeryüzü çevresi olsa gerek. Nitekim, kuzeye ve güneye giden yıldızlar aynı görünmüyor." [2]

Bu açıklamasıyla Aristoteles yerin küre şeklinde olduğunu söyler.

4. Gezegenler, Yer’in etrafında dolanır.

Yer, bir seri küre katmanını çevreler. İlk önce yerin elementleri su, hava ve ateş küreleri gelir. Ateş küresini ise saydam yapıda küreler çevreler. Gezegenler bu kürelere çakılı bir şekilde sıra ile taşınmaktadır. Bu gezegenlerin sırası;Ay, Merkür, Venüs, Güneş, Mars, Jüpiter, Satürn’dür. Bu küreler, cisimlerin hareketini sağlayan bir makinenin parçalarıdır. [3] Ay önemlidir ve evreni iki parçaya ayırır. Bunlar ayüstü ve ayaltı alemlerdir. Ayüstü alemin hareketlerinin dairesel olması önemlidir. Dairesel şekil Aristoteles’in felsefesinde önemlidir. Çünkü bu mükemmelliğin şeklidir. Bu özellik Ayüstü evrene bir mükemmellik sağlar.

5. Gezegenlerin hareketi daireseldir.

Evrende üç tür hareket vardır:

1. Evrenin orta noktası(merkez) uzaklaşan hareket.
2. Evrenin orta noktasına doğru hareket
3. Evrenin orta noktası etrafında hareket

Geometriye göre, dairesel hareketin oluşması için sabit bir noktaya gereksinim vardır. Bu nokta, merkez olan Yer’dir. Onun etrafında gezegenler hareket eder. Bu hareket varlık özelliğin mükemmelliğiyle sonsuzluğu gerektirir. Aristoteles’in evren anlayışı uzun süre astronomide ve yerle birlikte insanı merkez almakla birlikte din ve felsefede de büyük düşünsel değişimlere neden olmuştur. Ancak bu evren modeli gezegenlerin hareketlerini açıklamada yetersiz olmuştur. Bu sorunlar 17. yüzyıla kadar bir soru işareti olmakla birlikte bir sonraki büyük düşünsel ve bilimsel devriminde ayak sesleri olmuştur.

Evrim Ağacı'ndan Mesaj

Neden Desteğe İhtiyacımız Var?

Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor. Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak... Daha fazla göster

Aslında maddi destek istememizin nedeni çok basit: Çünkü Evrim Ağacı, bizim tek mesleğimiz, tek gelir kaynağımız. Birçoklarının aksine bizler, sosyal medyada gördüğünüz makale ve videolarımızı hobi olarak, mesleğimizden arta kalan zamanlarda yapmıyoruz. Dolayısıyla bu işi sürdürebilmek için gelir elde etmemiz gerekiyor.

Bunda elbette ki hiçbir sakınca yok; kimin, ne şartlar altında yayın yapmayı seçtiği büyük oranda bir tercih meselesi. Ne var ki biz, eğer ana mesleklerimizi icra edecek olursak (yani kendi mesleğimiz doğrultusunda bir iş sahibi olursak) Evrim Ağacı'na zaman ayıramayacağımızı, ayakta tutamayacağımızı biliyoruz. Çünkü az sonra detaylarını vereceğimiz üzere, Evrim Ağacı sosyal medyada denk geldiğiniz makale ve videolardan çok daha büyük, kapsamlı ve aşırı zaman alan bir bilim platformu projesi. Bu nedenle bizler, meslek olarak Evrim Ağacı'nı seçtik.

Eğer hem Evrim Ağacı'ndan hayatımızı idame ettirecek, mesleklerimizi bırakmayı en azından kısmen meşrulaştıracak ve mantıklı kılacak kadar bir gelir kaynağı elde edemezsek, mecburen Evrim Ağacı'nı bırakıp, kendi mesleklerimize döneceğiz. Ama bunu istemiyoruz ve bu nedenle didiniyoruz.

Destek Ol

Hazırlayan:Eric Rose

Referanslar
1. Gökyüzü Üzerine II, 286b-287a, sy. 10-15
2. Gökyüzü ÜzerineII, 296a-296-b, sy. 20-35
3. J.EL. Dreyer, History of Planetary System from Thales to Kepler, Dover 1952 sy. 112